Доверительный интервал для коэффициента регрессии
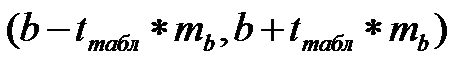 |
55. Множественная регрессия (multiple regression) включает одну зависимую переменную и две или больше независимых. Статистический метод, с помощью которого можно вывести математическую зависимость между двумя или больше независимыми переменными и зависимой переменной, выраженной с помощью интервальной или относительной шкалы.
56. Статистическая гипотеза, предположительное суждение о вероятностных закономерностях, которым подчиняется изучаемое явление. Как правило, Статистическая гипотеза определяет значения параметров закона распределения вероятностей или его вид. Статистическая гипотеза называется простой, если она определяет единственный закон распределения; в ином случае Статистическая гипотеза называется сложной и может быть представлена как некоторый класс простых Статистическая гипотеза Например, гипотеза о том, что распределение вероятностей является нормальным распределением с математическим ожиданием а = а0 и некоторой (неизвестной) дисперсией s2будет сложной, составленной из простых гипотез а = а0, 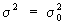 (а0 и
(а0 и 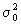 — заданные числа)
— заданные числа)
Ошибки I и II рода..
При проверке гипотез могут быть совершены ошибки 2-х родов:
1) Ошибкой I роданаз. такая ошибка, кот. совершается, если будет отвергнута правильная нулевая гипотеза. Вероятность ошибки I рода обозначается a и наз. уровнем значимости:
a £ 0,1
Отклонения нулевой гип. на уровне a = 0,05 означ, что мы не ошибаемся в 95 случаях из 100 или совершаем всё таки ошибку, принимая правильную гипотезу за ложную в 5 случаях из 100.
2) Ошибка II рода состоит в том, что будет принята неправильная нулевая гипотеза H0 . Вер-сть ошибки II рода обозначается b .
Стат. критерием (значимости) наз. СВ X, кот. является ф-цией выборки K=К(х1, х2, х3,…,хn) (статистической) и служит для проверки гипотезы, с ее помощью принимается решение о принятии или отвержении гипотезы Н0.
Критическая область – совок – ть значений критерия, при которых нулевую гипотезу отвергают.
Точки, разделяющие критическую область и область допустимых значений, называются критическими точками (или границами критической области).
57.Мощностью критерия kназ. вер-сть М несовершения ошибки II рода: М= 1-b. Др. словами, мощность критерия – это вер-сть того, что нулевая гип. будет отвергнута, если верна конкурируюшая гип. H1.
 Если n®¥, b®1, то критерий наз. критерием согласия.
Если n®¥, b®1, то критерий наз. критерием согласия.
При данном уровне значимости a из всех критериев лучшим будет тот, у кот. вер-сть ошибки II рода b будет минимальной.
 После выбора критерия k множ-во всех его значений распадается на 2 непересекающихся подмножеств: критическую область W и О.Д.З. (или обл. принятия гипотезы).
После выбора критерия k множ-во всех его значений распадается на 2 непересекающихся подмножеств: критическую область W и О.Д.З. (или обл. принятия гипотезы).
ОДЗ W

 k Если значение критерия kнабл. попадает в критич.
k Если значение критерия kнабл. попадает в критич.
область, то нулевая гипотеза отвергается в пользу конкурирующей гип. H1. Если kнабл. попадает в О.Д.З., то нет оснований отвергнуть нулевую гипотезу, т.е. рез-ты опыта согласовываются с гипотезой.
| Отыскание правосторонней критической области |
Как найти критическую область? Для определения начнем с нахождения правосторонней критической области, которая определяется неравенством К > Ккр, где Ккр > 0. Для отыскания правосторонней критической области достаточно найти критическую точку. Следовательно, возникает новый вопрос: как ее найти? С этой целью задаются достаточно малой вероятностью – уровнем значимости. Затем ищут критическую точку Ккр, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий К примет значение, большее Ккр, была равна принятому значению уровня значимости: Р ( К > Ккр) = 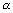 . Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию. Когда критическая точка уже найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что Кнабл > Ккр, то нулевую гипотезу отвергают; если же Кнабл < Ккр, то нет оснований, чтобы отвергнуть нулевую гипотезу. Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение Р ( К > Ккр) = . Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию. Когда критическая точка уже найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что Кнабл > Ккр, то нулевую гипотезу отвергают; если же Кнабл < Ккр, то нет оснований, чтобы отвергнуть нулевую гипотезу. Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение Р ( К > Ккр) = 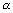 . Поскольку вероятность события К > Ккр мала ( . Поскольку вероятность события К > Ккр мала ( 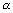 – малая вероятность), такое событие при справедливости нулевой гипотезы в силу принципа практической невозможности маловероятных событий в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше Ккр, то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование Р ( К > Ккр) = – малая вероятность), такое событие при справедливости нулевой гипотезы в силу принципа практической невозможности маловероятных событий в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше Ккр, то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование Р ( К > Ккр) = 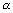 определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они составляют правостороннюю критическую область. Наблюдаемое значение критерия может оказаться большим Ккр не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они составляют правостороннюю критическую область. Наблюдаемое значение критерия может оказаться большим Ккр не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости 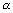 . . |
| Отыскание левосторонней и двусторонней критических областей |
Отыскание левосторонней и двусторонней критических областей сводится (так же как и для правосторонней) к нахождению соответствующих критических точек. Левосторонняя критическая область определяется неравенством: К < Ккр ( Ккр < 0). Критическую точку находят, исходя из требования, чтобы при справедливости нулевой гипотезы вероятность того, что критерий имеет значение, меньшее Ккр, была равна принятому уровню значимости: Р ( К < Ккр) = 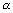 . Двусторонняя критическая область определяется неравенствами: К< К1, К > К2. Критические точки находят, исходя из требования, чтобы при справедливости нулевой гипотезы сумма вероятностей того, что критерий примет значение, меньшее К1 и большее К2, была равна принятому уровню значимости: Р ( К < К1) + Р ( К > К2) = . Двусторонняя критическая область определяется неравенствами: К< К1, К > К2. Критические точки находят, исходя из требования, чтобы при справедливости нулевой гипотезы сумма вероятностей того, что критерий примет значение, меньшее К1 и большее К2, была равна принятому уровню значимости: Р ( К < К1) + Р ( К > К2) = 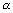 . Ясно, что критические точки могут быть выбраны множеством способов. Если распределение критерия симметрично относительно нуля и имеются основания выбирать симметричные относительно нуля точки Ккр и Ккр (К > 0), то Р ( К < -Ккр) = Р ( К > Ккр). Зная Р ( К < К1) + Р ( К > К2) = . Ясно, что критические точки могут быть выбраны множеством способов. Если распределение критерия симметрично относительно нуля и имеются основания выбирать симметричные относительно нуля точки Ккр и Ккр (К > 0), то Р ( К < -Ккр) = Р ( К > Ккр). Зная Р ( К < К1) + Р ( К > К2) = 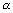 , получим Р ( К > Ккр) = , получим Р ( К > Ккр) = 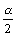 . Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам. . Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам. |
58. . Критерий Фишера.
Критерий используется для сравнения дисперсий двух выборок с нормальным распределением.
Сравнения дисперсий двух выборок производятся по отношению большей по величине дисперсии(записывается в числителе) к меньшей (записывается в знаменателе). Поэтому значения критерия больше или равно 1,0.
Гипотезы
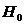 : Дисперсия выборке 1 не отличается от дисперсии в выборке 2
: Дисперсия выборке 1 не отличается от дисперсии в выборке 2
 : Дисперсия выборке 1 отличается от дисперсии в выборке 2
: Дисперсия выборке 1 отличается от дисперсии в выборке 2
Ограничения
Данные в выборках должны быть измерены по шкале интервалов или по шкале отношений.
Обе сравниваемые выборки должны иметь нормальный закон распределения.
Алгоритм.
- Предварительно проверяется нормальность закона распределения по одному из критериев согласия.
- Рассчитывается средне арифметические значения
 и
и  для каждой выборки по формуле
для каждой выборки по формуле 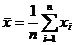 где
где  – значение i-го результата наблюдения
– значение i-го результата наблюдения - Рассчитываются значение
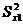 и
и  –дисперсии для каждой выборке по формуле
–дисперсии для каждой выборке по формуле 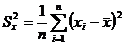
- Определяется число степеней свободы по выборкам:
 - по первой выборке и
- по первой выборке и 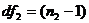 по второй выборке.
по второй выборке.
- Рассчитывается
 - эмпирическое значение критерия по одной из формул:
- эмпирическое значение критерия по одной из формул:
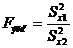 или
или  с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
- Найденное эмпирическое значение критерия Фишера
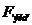 сравнивается критическим значением
сравнивается критическим значением 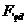 (по таблице 2 приложения) для данного числа степеней свободы
(по таблице 2 приложения) для данного числа степеней свободы  .
.
Если эмпирическое значение 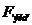 <
< 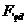 , то нулевая гипотеза
, то нулевая гипотеза 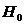 о равенстве дисперсий в выборках при заданном уровне значимости
о равенстве дисперсий в выборках при заданном уровне значимости 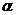 принимается.
принимается.
59. Проверка гипотез о законе распределения (критерии Пирсона)
Существует несколько критериев согласия для проверки законов распределения случайной величины. Это критерии Колмогорова, Смирнова, Пирсона и др. Мы остановимся лишь на критерии Пирсона это наиболее часто употребляемый критерий для проверки закона распределения случайной величины.
Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения.
Проверка гипотезы о нормальном распределении.
Пусть получена выборка достаточно большого объема п с большим количеством различных значений вариант. Доя удобства ее обработки разделим интервал от наименьшего до наибольшего из значений вариант на s равных частей и будем считать, что значения вариант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала. Подсчитав число вариант, попавших в каждый интервал, составим так называемую сгруппированную выборку:
варианты..х1 х2 хs
частоты.п1 п2 пs ,
где хi значения середин интервалов, а пi число вариант, попавших в i-й интервал (эмпирические частоты).
По полученным данным можно вычислить выборочное среднее и выборочное среднее квадратическое отклонение ?В. Проверим предположение, что генеральная совокупность распределена по нормальному закону с параметрами M(X) = , D(X) = . Тогда можно найти количество чисел из выборки объема п, которое должно оказаться в каждом интервале при этом предположении (то есть теоретические частоты). Для этого по таблице значений функции Лапласа найдем вероятность попадания в i-й интервал:
,
где аi и bi- границы i-го интервала. Умножив полученные вероятности на объем выборки п, найдем теоретические частоты: пi =n?pi. Наша цель сравнить эмпирические и теоретические частоты, которые, конечно, отличаются друг от друга, и выяснить, являются ли эти различия несущественными, не опровергающими гипотезу о нормальном распределении исследуемой случайной величины, или они настолько велики, что противоречат этой гипотезе. Для этого используется критерий в виде случайной величины
. (1)
Смысл ее очевиден: суммируются части, которые квадраты отклонений эмпирических частот от теоретических составляют от соответствующих теоретических частот. Можно доказать, что вне зависимости от реального закона распределения генеральной совокупности закон распределения случайной величины (1) при стремится к закону распределения с числом степеней свободы k = s 1 r, где r число параметров предполагаемого распределения, оцененных по данным выборки. Нормальное распределение характеризуется двумя параметрами, поэтому k = s 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием
(2)
где ? уровень значимости. Следовательно, критическая область задается неравенством а область принятия гипотезы - .
Итак, для проверк
