Генеральная совокупность и выборочная совокупность

В выборочном наблюдении используются понятия «генеральная совокупность» -- изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и «выборочная совокупность» -- случайно выбранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т.е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности.

Характеристиками генеральной и выборочной совокупностей могут служить средние значения изучаемых признаков, их дисперсии и средние квадратические отклонения, мода и медиана и др. Исследователя могут интересовать и распределение единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.

Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода, суть которого состоит в получении первичных данных при наблюдении выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении.

Репрезентативность выборки обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает для каждой единицы совокупности одинаковую вероятность быть выбранной для наблюдения для любой выборки заданного объема. Таким образом, цель выборочного метода -- сделать вывод о значении признаков генеральной совокупности на основе информации случайной выборки из этой совокупности.

Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные

1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком.

2. Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в маркетинговых исследованиях достаточно часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.

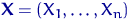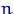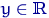Эмпирической функцией распределения, построенной по выборке объема , называется случайная функция , при каждом равная

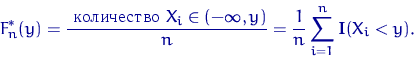
В отличие от эмпирической функции распределения выборки, функцию распределения 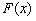генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция 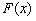определяет вероятность события X<x, тогда как эмпирическая – относительную частоту этого же события.

При росте n относительная частота события X<x, т.е. 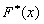стремится по вероятности к вероятности 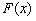этого события. Иными словами:

.

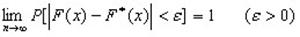50.Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины

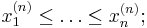
равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λ_m = m / n называется рангом порядковой статистики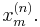

Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид

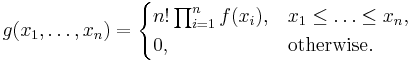
Характеристики вариационного ряда. При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, силу и величину вариации. К ним относятся медиана и иные квантили разного уровня, мода, размах или амплитуда вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия и другие показатели.

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки 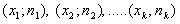. Для построения полигона частот на оси абсцисс откладывают варианты 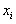, а на оси ординат – соответствующие им частоты 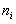и соединяют точки 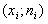отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .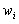

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала 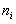– сумму частот вариант, попавших в i–й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению 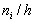. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) 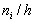. Площадь i–го прямоугольника равна 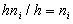– сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

В случае гистограммы относительных частот по оси ординат откладываются относительные частоты 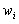, на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте 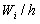. Площадь i–го прямоугольника равна относительной частоте вариант 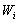, попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

51. Оценкой 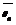параметра 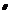называется любая функция от значе­ний выборки 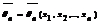, т.е. статистика. Оценка является несмещённой, если 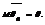Если для любого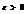 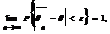то оценка 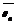называется состоятельной. Оценкой качества несмещенной оценки является ее диспер­сия. Несмещенная оценка 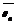называется эффективной, если ее дисперсия 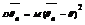является наименьшей среди дисперсий всех возможных оценок параметра 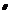, вычисленных по одному и тому же объему выбор­ки п. Оценки 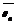называются точечными, так как они оценивают одно численное значение параметра 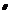(точку). Точечная оценка 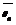параметра 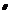дает лишь некоторое при­ближенное значение 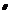. Чтобы получить представление о точно­сти и надежности оценки, используют интервальную оценку параметра.

Интервальной оценкой параметра 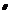называется интервал (α, β), который с заданной вероятностью γ накрывает неизвест­ное значение параметра 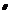. Такой интервал (α, β) называется доверительным интерва­лом, а вероятность γ — доверительной вероятностью, или уровнем надежности. Обычно доверительный интервал симметричен относительно оценки 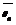, тогда он определяется фор­мулой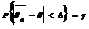

и имеет вид 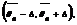т.е. неравенства 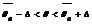выполняется с вероятностью γ. Наибольшее отклонение Δ выборочного значения параметра от его истинного значения называется предельной ошибкой вы­борки.

52.Построение доверительных интервалов.

1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии.

Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего 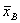оценить ее математическое ожидание а. Будем рассматривать выборочное среднее 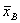как случайную величину 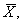а значения вариант выборки х₁, х₂,…, х_п как одинаково распределенные независимые случайные величины Х₁, Х₂,…, Х_п, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М( 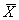) = а, 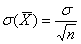(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства 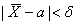. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:

р ( 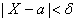) = 2Ф 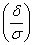. Тогда , с учетом того, что 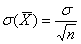, р ( 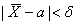) = 2Ф =

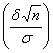=2Ф( t ), где 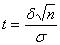. Отсюда 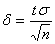, и предыдущее равенство можно переписать так:

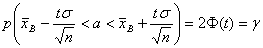. (18.1)

Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал 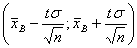, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.

Пример. Найдем доверительный интервал для математического ожидания нормально распреде-ленной случайной величины, если объем выборки п = 49, 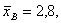σ = 1,4, а доверительная вероятность γ = 0,9.

Определим t, при котором Ф(t) = 0,9:2 = 0,45: t = 1,645. Тогда

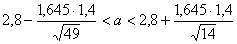, или 2,471 < a < 3,129. Найден доверительный интервал, в который попадает а с надежностью 0,9.

2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии.

Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания построим новую случайную величину

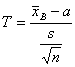, (18.2)

где 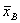- выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента (см. лекцию 12) с k = n – 1 степенями свободы.

Поскольку плотность распределения Стьюдента 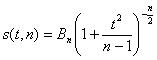, где 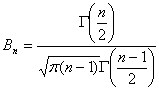, явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- t_γ , t_γ ), учитывая четность плотности распределения, следующим образом: 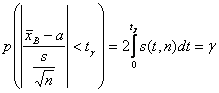. Отсюда получаем:

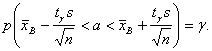(18.3)

Таким образом, получен доверительный интервал для а, где t_γ можно найти по соответствую-щей таблице при заданных п и γ.

Пример. Пусть объем выборки п = 25, 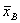= 3, s = 1,5. Найдем доверительный интервал дляа при γ = 0,99. Из таблицы находим, что t_γ(п = 25, γ = 0,99) = 2,797. Тогда 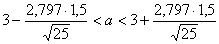, или 2,161< a < 3,839 – доверительный интервал, в который попадает а с вероятностью 0,99.

Доверительный интервал

Доверительный интервал - это допустимое отклонение наблюдаемых значений от истинных. Размер этого допущения определяется исследователем с учетом требований к точности информации. Если увеличивается допустимая ошибка, размер выборки уменьшается, даже если уровень доверительной вероятности останется равным 95%.

Доверительный интервал показывает, в каком диапазоне расположатся результаты выборочных наблюдений (опросов). Если мы проведем 100 одинаковых опросов в одинаковых выборках из единой генеральной совокупности (например, 100 выборок по 1000 человек в каждой в городе с населением 5 миллионов человек), то при 95%-й доверительной вероятности, 95 из 100 результатов попадут в пределы доверительного интервала (например, от 28% до 32% при истинном значении 30%).

53. ТОЧЕЧНАЯ ОЦЕНКА

- статистическая оценка, значения к-рой суть точки во множестве значений оцениваемой величины.
Пусть по реализации 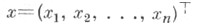случайного вектора 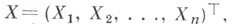принимающего значения в выборочном пространстве 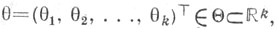надлежит оценить неизвестный параметр 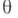(или нек-рую функцию Тогда любая статистика Т _n=Т _п (Х),осуществляющая отображение множества 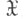в 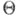(или в множество значений функции 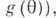наз. точечной оценкой параметра (оцениваемой функции Важными характеристиками Т. о. Т _п являются ее математич. ожидание

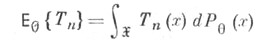
и дисперсионная матрица (ковариационная матрица)

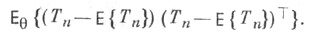
Вектор 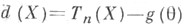наз. вектором ошибок Т. о. Т _п. Если

- нулевой вектор при всех то говорят, что Т _п является несмещенной оценкой функции 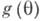или что Т _п лишена систематич. ошибки, в противном случае Т. о. Т _п наз. смещенной, а вектор 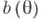- смещением или систематической ошибкой Т. <о. Качество Т. о. определяется с помощью функции риска.

Введем понятие интервальной оценки неизвестного параметра

генеральной совокупности (или случайной величины , определенной на

множестве объектов этой генеральной совокупности). Обозначим этот

параметр через . По сделанной выборке по определенным правилам

найдем числа 1 и 2, так чтобы выполнялось условие:

P(1< < 2) =P ((1; 2)) =

Числа 1 и 2 называются доверительными границами, интервал (1, 2)

— доверительным интервалом для параметра . Число называется

доверительной вероятностью или надежностью сделанной оценки.

Сначала задается надежность. Обычно ее выбирают равной 0.95,

0.99 или 0.999. Тогда вероятность того, что интересующий нас параметр

попал в интервал (1, 2) достаточно высока. Число (1 + 2) / 2 – середина

доверительного интервала – будет давать значение параметра с

точностью (2 – 1) / 2, которая представляет собой половину длины

доверительного интервала.

Границы 1 и 2 определяются из выборочных данных и являются

функциями от случайных величин x1, x2,..., xn

, а следовательно – сами

случайные величины. Отсюда – доверительный интервал (1, 2) тоже

случаен. Он может покрывать параметр или нет. Именно в таком смысле

нужно понимать случайное событие, заключающееся в том, что

доверительный интервал покрывает число

54. Выборочный коэффициент корреляции рассчитывается по формуле

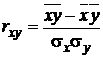
Здесь

, ,

.

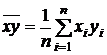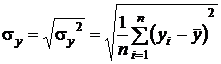Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции r_xh, характеризующего генеральную совокупность.