Глава 1. основы сопротивления материалов

ВВЕДЕНИЕ

Учебная дисциплина«Механика» состоит из трех разделов:

«Теоретическая механика», «Сопротивление материалов» и «Детали машин».

В данном учебном пособии компактно и в доступной форме излагается курс сопротивления материалов. Объем представленного материала соответствует Примерной программе дисциплины «Механика» для групп специальностей с объемом 200 учебных часов. Для групп с меньшим объемом часов можно выбрать необходимый материал с программами дисциплины для запланированного количества учебных часов и примерного уровня требований.

В пособии рассмотрены основные положения курса сопротивления материалов для простых видов нагружения: растяжения-сжатия, кручения, изгиба. Сформулированы условия прочности. Во второй части курса изложены темы: перемещения при изгибе, статически неопределимые системы, устойчивость стержневых систем. Курс завершается разделами, использующие понятие сложного напряженного состояния (основы теории напряженного и деформированного состояний, критерии пластичности и разрушения, простейшие задачи при сложном напряженном состоянии, прочность при переменных напряжениях).

Данное пособие будет особенно полезно при самостоятельной работе над курсом студентам, изучающим данный раздел механики, где согласно учебным планам выделяется только один семестр. Рекомендуется студентам заочной формы обучения и студентам ИДПО, благодаря простой и доступной форме изложения.

Глава 1. ОСНОВЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ

Предмет «Сопротивление материалов»

Сопротивление материалов – наука о прочности, жесткости и устойчивости элементов конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые, надежные размеры деталей машин и различных строительных сооружений. Основные положения сопротивления материалов опираются на законы и теоремы общей механики, математики и физики. Основной базой является теоретическая механика, которая изучает равновесие и движение абсолютно твердых тел. В отличие от теоретической механики, в сопротивлении материалов рассматриваются деформируемые тела, которые могут менять размеры и форму под действием внешних сил.

Объект курса

Любая конструкция состоит из элементов. Элементы конструкций:

1) Брус (стержень). Брусом называется твердое тело, одно из измерений которого (длина) значительно превышает размеры поперечного сечения (рис. 1.1,а).

Рис. 1.1. Модели формы элементов конструкции:

а — стержень; б — кольцо; в — круглая пластинка; г — оболочка; д — массив

2) Оболочка, пластина. Оболочкой называется твердое тело, одно измерение которого (толщина) мало по сравнению с двумя другими (рис. 1.1,г). Геометрическое место точек, равноудаленных от наружной и

внутренней поверхностей оболочки, называется срединной поверхностью.

Оболочка, срединная поверхность которой представляет собой плоскость, называется пластиной (рис. 1.1,б, в).

3) Массив. Все три измерения одного порядка (рис. 1.1,д).

В сопротивлении материалов главное внимание уделяется расчету стержней (брусьев). Расчетами пластин, оболочек, массивов занимается теория упругости.

Внешние силы

Если конструкция рассматривается изолированно от окружающих тел, то действие последних на конструкцию заменяется силами, которые называются внешними.

Различают:

Сосредоточенные силы – передаются на конструкцию через небольшую площадку, т.е. можно практически условно считать, что они приложены в точке (рис. 1.2). К числу таких сил можно отнести давление колеса на рельс и т.д. Из приведенного примера видно, что понятие сосредоточенной силы является условным. Одна и та же нагрузка в зависимости от поставленной задачи может быть схематизирована по-разному.

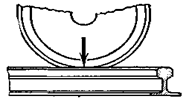
Рис. 1.2

Распределенная нагрузка – передается на сооружение через определенную площадь и измеряется в единицах силы, отнесенной к единице площади (кн/м², кн/см², н/мм²). К числу таких нагрузок относится давление сыпучих материалов и жидкости на стенки резервуаров (рис. 1.3,а), давление воды на пластину (рис. 1.3,б) и т.п.

Рис. 1.3

Для стержневых систем распределенную по площади нагрузку 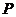(рис. 1.4,а) – обычно заменяют погонной 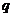(рис. 1.4,б).

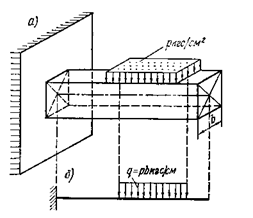
Рис. 1.4

где 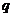— погонная нагрузка, 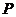— нагрузка, распределенная по площади, 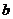— ширина балки.

По времени действия – нагрузки подразделяются:

а) статические – нагрузки, приложенные к сооружению довольно медленно, когда ускорениями масс сооружений, а, следовательно, и силами инерции можно пренебречь.

б) динамические – нагрузки изменяемые во времени: удар копра, несбалансированный двигатель. Эти нагрузки дают динамический эффект, когда ускорениями движения масс пренебречь нельзя, а, следовательно, должны учесть силу инерции.

Основные понятия и гипотезы (допущения)

Под действием внешних нагрузок отдельные частицы тела перемещаются относительно друг друга. Как следствие тело изменяет свои размеры и форму. Эти изменения и называется деформацией.

Если силы, вызвавшие деформацию уменьшать и затем полностью снять, то тело будет стремиться приобрести первоначальную форму. Деформации полностью или частично исчезнут. Свойство тел деформироваться под нагрузкой и затем после устранения сил восстанавливать свое первоначальное состояние называют упругостью. Часть деформации, которая исчезает после снятия нагрузок, называют упругой, а ту часть, которая остается, называют остаточной деформацией. Появление остаточной деформации связано с так называемой пластичностью.

У некоторых материалов упругие свойства одинаковы во всех направлениях. Такие тела называют изотропными. Наряду с этим встречаются анизотропные тела, у которых свойства в различных направлениях разные.

Сопротивление материалов рассматривает идеализированное тело (абстрактное) и наделяет определенными свойствами. Гипотеза о сплошном и однородном строении материала.

Под сплошным понимаем материал, который не имеет никаких пустот, что позволяет применять анализ бесконечно малых величин.

Под однородностью понимается то, что механические свойства тела в окрестностях точки не зависят от размеров рассматриваемого элемента.

Эпюры внутренних усилий

При расчете стержней (балок) на прочность необходимо уметь строить графики изменений силовых факторов по длине бруса 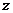. Эти графики называются эпюрами.

При растяжении (сжатии) строят .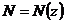

При кручении

При построении графиков нормальную силу считают положительной, если она вызывает растяжение бруса.

Крутящий момент считают положительным, если смотреть со стороны внешней нормали к сечению, наблюдатель видит момент, направленный против часовой стрелки.

Диаграмма растяжения

Для изучения свойств материалов под нагрузкой производят испытания образцов, изготовленных из этих материалов. Эти испытания проводят с целью определить числовые характеристики, позволяющие оценить прочность и пластичность материала. Такие характеристики называют механическими.

Важнейшие механические свойства реальных тел могут быть выявлены из опытов на растяжение — сжатие. Эти опыты проводят на специальных машинах. На рис. 2.10 приведена схема одной из испытательных машин ZD-10/90.

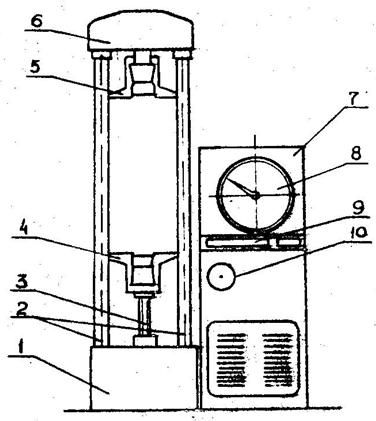
Рис. 2.10

Данная машина предназначена для проведения испытаний на растяжение, сжатие и изгиб с максимальным усилием до 100 кН. Она состоит из самой машины и пульта управления. Основные узлы: 1 — основание; 4, 5 — нижняя и верхняя траверса; 6 — поперечная траверса; 7 — пульт управления. Основание (1) выполнено в виде литой конструкции, где установлены колонны (2) и червячный привод. Приводной двигатель расположен на основании пульта управления (7), который через клиноременные шкивы передает вращение на вал червячной передачи. Червячное колесо надето на гайку ходового винта (3). Ходовой винт соединен через съемный шпиндель с нижней траверсой (4). Направление движения траверсы осуществляется по ходовым каткам. Верхняя траверса (5) закреплена на поперечной траверсе (6) и жестко соединена с датчиком измерения усилия. На верхней и нижней траверсе устанавливаются захваты для испытываемых образцов. На пульте управления (7) размещаются: стрелочный динамометр (8), панель управления, ручной привод (10), регистрирующее устройство (9). Общий вид машины представлен на рис. 2.11.

Рис. 2.11

Испытания проводят на стандартных образцах круглой или плоской формы (рис. 2.12,а, б).

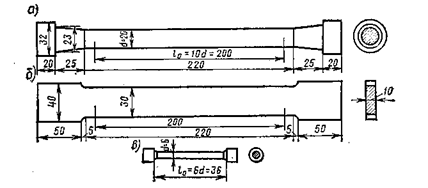
Рис. 2.12

На рис. 2.13 показана типичная для углеродистой стали диаграмма растяжения, полученная в результате испытания.

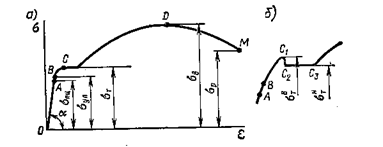
Рис. 2.13

Напряжения вычисляем по формуле 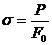, 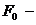первоначальная площадь.

Деформации вычисляем по формуле:

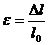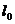, где — первоначальная длина образца.

На участке 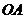справедлив закон Гука 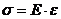, т.е. напряжения, растут прямо пропорционально деформации. Пределом пропорциональности 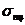называют наибольшее напряжение, при котором справедлив закон Гука. (Для стали Ст3 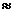21 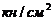). Угол наклона этой прямой можно определить как .

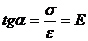Выше точки 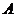диаграмма искривлена и нарушается закон Гука. Очень близко к точке 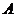, на криволинейном участке, можно отметить точку 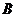, соответствующую пределу упругости. Пределом упругости 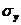называют максимальное напряжение, при котором в материале не возникает остаточной деформации, определяемой при разгрузке. По Госту условным пределом упругости называют напряжение, при котором остаточная деформация достигает 0,05 % и обозначают 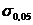. Точка 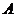находится вблизи точки 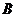поэтому их часто считают совпадающими.

Начиная с некоторой точки 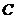диаграмма имеет почти горизонтальный участок, на нем деформации растут без увеличения нагрузки 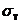. Пределом текучести называется напряжение при котором деформации растут без увеличения напряжения. Для стали Ст3

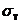=24 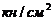. Площадка текучести наблюдается только для малоуглеродистых сталей. Большинство материалов не имеет площадки текучести.

После площадки текучести нагрузка на образец, а, следовательно, напряжения, вновь начинают расти. Происходит самоупрочение материала до точки 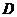. Пределом прочности (временным сопротивлением) 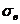называют отношение наибольшей нагрузки, выдерживаемой образцом, к первоначальной площади поперечного сечения. Предел прочности является некоторой условной характеристикой, т.к. она не является напряжением, при котором материал разрушается, т.к. площадь поперечного сечения при разрушении значительно меньше (для стали Ст3 ).

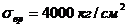До точки 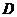деформация стержня является равномерной. После точки 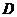она концентрируется в одном месте (наиболее слабом) начинает образовываться шейка — местное сужение образца (рис. 2.14,а). Наконец в точке 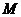наступает разрыв образца. Этой точке соответствует 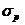— условное напряжение при разрыве.

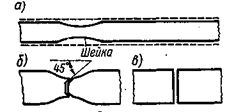
Рис. 2.14

При разрыве на одной части образца виден конус, а на другой кратер (рис. 2.14,б): угол с осью 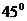. Такая форма разрушения образцов из малоуглеродистой стали, показывает, что разрушение связано со сдвигом по площадкам, наклоненным под 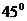к оси стержня, где касательные напряжений будут наибольшими. Такой тип разрушения пластичных материалов называют разрушение путем сдвига.

Для сравнения диаграмм растяжения на рис. 2.15 представлены диаграммы некоторых других материалов.

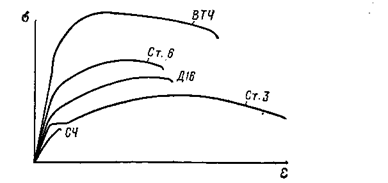
Рис. 2.15

Сталь Ст.6 по сравнению со сталью Ст.3 обладает значительно более высокими характеристиками прочности. Площадка текучести у высокопрочных сталей, как правило, отсутствует или имеет очень малую протяженность. Высокими механическими свойствами обладает титановый сплав ВТ4. Диаграмма растяжения чугуна (С4) вообще не имеет прямого участка, она искривляется уже в самом начале. Чугун, строго говоря, вообще не подчиняется закону Гука.

Диаграмма сжатия

Для изучения “поведения” материалов при сжатии строятся диаграммы сжатия. Испытания металлов на сжатие производятся на образцах в виде цилиндров, высота которых равна их диаметру (обычно d=h=20 мм). Для других материалов (дерево, цемент, бетон) применяют образцы в виде кубиков.

Рассмотрим диаграммы сжатия, стали и чугуна. Для наглядности изобразим их на одном рисунке с диаграммами растяжения (рис. 2.16).

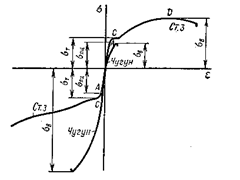
Рис. 2.16

При испытании Ст3 на сжатие σ_нц , σ_у, σ_т примерно такие же как и их растяжение. Затем образец в силу наличия трения по торцам приобретает форму бочонка и дальше расплющивается (рис. 2.17), но разрушить его не удается, поэтому предел прочности установить нельзя. Условно принимают предел прочности при сжатии такой же, как и растяжения.

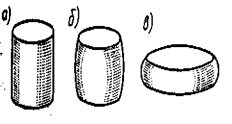
Рис. 2.17

Диаграмма сжатия чугуна по форме напоминает диаграмму растяжения. Она криволинейна с самого начала. Однако предел прочности при сжатии чугуна примерно в 4-5 раз выше предела прочности при растяжении. При испытании чугунного образца (рис. 2.18, а) продольные деформации его незначительны. Образец несколько выпучивается в средней части, принимая слегка бочкообразную форму, после чего в нем появляются трещины под углом примерно 45⁰ к оси по площадкам с наибольшими касательными напряжениями (рис. 2.18, б).

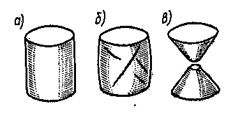
Рис. 2.18

В это время нагрузка резко падает и диаграмма обрывается. В момент разрушения боковые части образца отделяются и он принимает вид двух усеченных конусов (рис. 2.18, в).

Основные понятия

При растяжении (сжатии) мы встречались с простейшей геометрической характеристикой поперечного сечения — площадью 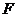. При изгибе и кручении этой характеристики недостаточно.

Возьмем, к примеру, брус прямоугольного поперечного сечения с площадью 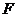, приложим к свободному концу силу 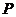(рис. 4.1)

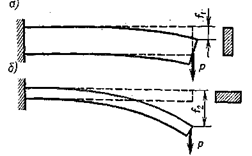
Рис. 4.1

Расположим его сечение по отношению к нагрузке как показано на рис. 4.1,а,б. В зависимости от ориентации сечения прогибы 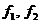будут разными.

Вывод: площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу. Необходимо привлекать к рассмотрению более сложные геометрические характеристики.

Статические моменты сечения

Возьмем некоторое поперечное сечение бруса (рис. 4.2)

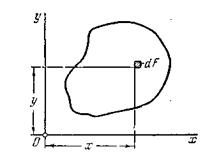
Рис. 4.2

Свяжем его с системой координат 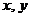и рассмотрим два следующих интеграла

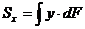
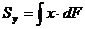(4.1)

Индекс 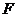у интеграла означает, что интегрирование ведется по всей площади сечения.

Первый интеграл называется статическим моментом сечения относительно оси 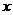, а второй статическим моментом относительно оси 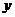. Размерность — .

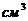При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осе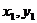й и 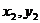(рис. 4.3).

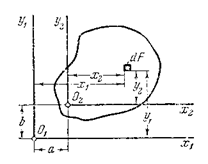
Рис. 4.3

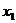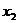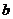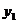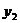Пусть расстояние между осями и равно , а между и равно 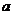. Дано: 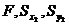. Требуется определить .

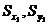Очевидно, что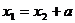

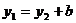
Искомые статические моменты равны

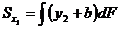
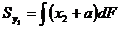
Или .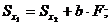

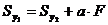Рассмотрим подробнее, например, первое из полученных выражений

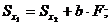
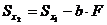
Величина 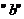может быть как положительной, так и отрицательной. Всегда можно подобрать 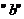так, причем единственным образом, чтобы,

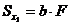, тогда 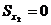. Ось, относительно которой статический момент равен “0”, называется центральной.

Расстояние до центральной оси от некоторой произвольной 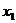равно

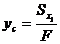, (4.2)

аналогично

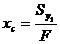. (4.3)

Таким образом, с помощью формул (4.2), (4.3) можно найти центр тяжести любой фигуры.

Глава 5. ИЗГИБ

Основные понятия

Под изгибом понимается такой вид нагружения стержня, когда в его поперечных сечениях возникают изгибающие моменты. Если изгибающий момент является единственным силовым фактором, то изгиб называется чистым. Большей частью в поперечных сечениях бруса наряду с изгибающими моментами возникают и поперечные силы. В этом случае изгиб называют поперечным. В дальнейшем встретимся с более сложными видами изгиба.

Брус, работающий на изгиб, обычно называют балкой. Кроме балок на изгиб работают элементы рам. Рамой называется конструкция, состоящая из стержней, элементы которой работают преимущественно на изгиб.

Ранее мы уже познакомились с внутренними силовыми факторами 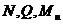, возникающими при изгибе, и строили их эпюры. Теперь перейдем к исследованию напряжений, возникающих при изгибе.

5.2. Дифференциальные зависимости между 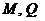и

И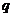згибающий момент 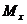, поперечная сила 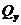и интенсивность внешней нагрузки 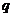связаны между собой определенной зависимостью. Вырежем из балки, загруженной распределенной нагрузкой 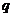, изменяющейся по какому—либо закону (рис. 5.1,а), элемент длиной 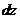(рис. 5.1,б).

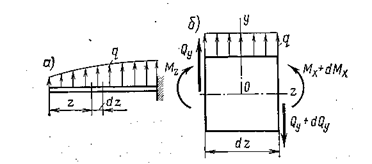
Рис. 5.1

Нагрузку считают положительной, если она направлена вверх; на протяжении длины 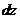ее считают равномерно распределенной.

Составим два уравнения равновесия элемента:

.

.

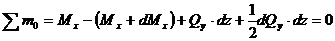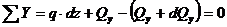В первом уравнении произведением 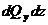как величиной второго порядка малости по сравнению с остальными слагаемыми можно пренебречь.

После элементарных преобразований из приведенных выше уравнений находим

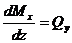. (5.1)

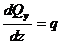. (5.2)

Из двух полученных дифференциальных зависимостей вытекает третья:

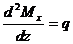. (5.3)

Зависимости (5.1) и (5.2) часто используются при проверке правильности построения эпюр моментов и поперечных сил.

Чистый косой изгиб

Изгиб называется косым, если плоскость действующих сил проходит через ось балки, но не совпадает ни с одной из главных осей сечения.

Его удобнее всего рассматривать как одновременный изгиб бруса в двух главных плоскостях 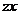и 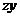(рис. 5.13).

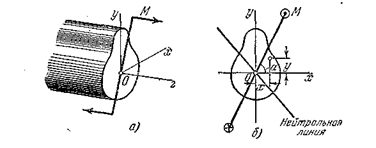
Рис. 5.13

Для этого изгибающий момент 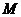раскладывается на составляющие относительно осе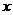й и :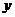

, .

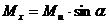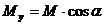Таким образом, косой изгиб сводится к двум плоским изгибам относительно осе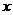й, и 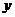. Изгибающие моменты считаются положительными, если они вызывают растяжение в первой четверти.

Нормальные напряжения в точке имеющей координаты 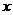и 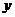будут равны сумме напряжений от 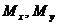, т.е.

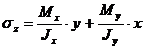(5.13)

Следовательно, как при простом изгибе нормальные напряжения при косом изгибе образуют плоскость.

Уравнение нейтральной линии получим, положив в (5.13) .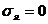

.

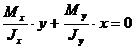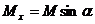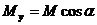После подстановки и получим

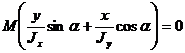, т.к. 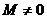, то 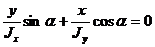или окончательно уравнение нейтральной линии получим в виде:

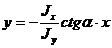. (5.14)

Легко установить, что при косом изгибе нейтральная линия не перпендикулярна плоскости изгибающего момента.

Угловой коэффициент 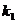следа плоскости момента (рис. 5.13,б) представляет собой тангенс угла ,

.

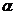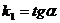Угловой коэффициент нейтральной линии равен

.

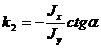Т.к. в общем случае 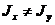, то условие перпендикулярности прямых, известное из аналитической геометрии, не соблюдается, поскольку

.

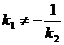Поэтому нейтральная линия не перпендикулярна к плоскости момента, а несколько повернута в сторону минимального момента инерции. Брус «предпочитает» изгиб не в плоскости изгибающего момента, а в некоторой другой плоскости, где плоскость на изгиб будет меньше.

Т.к. эпюра нормальных напряжений в сечении линейка, то максимальные напряжения возникают в точке, наиболее удаленной от нейтральной линии. Пусть координаты этой точки будут 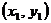тогда:

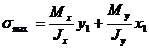. (5.15)

Условие прочности можно записать в виде:

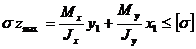. (5.16)

Если сечение имеет простую форму, то наиболее удаленные точки находятся сразу, если сложную то, вычертив сечение в масштабе (рис. 5.14), наносится положение нейтральной линии, и графически находится наиболее удаленная точка (рис. 5.14).

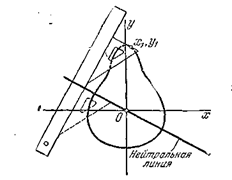
Рис. 5.14

Способ Верещагина

Основным недостатком при определении перемещений с помощью интегралов Мора является необходимость составлять аналитические выражения подынтегральных функций и дальнейшего их интегрирования. Это особенно неудобно при большом количестве участков, т.к. приводит к громоздким вычислениям.

Если брус состоит из прямых участков с постоянной, в пределах каждого участка жесткостью, то операцию вычисления интегралов Мора можно упростить. Это упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках бруса всегда будут линейными.

Пусть на участке длиной 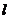нужно взять интеграл от произведения двух функций

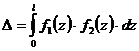(6.9)

при условии, что по крайне мере одна из функций — линейная. Пусть 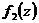— линейная, тогда 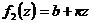(рис.6.5).

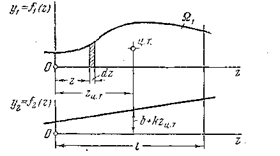
Рис. 6.5

Тогда выражение (6.9) примет вид 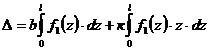. Первый из интегралов представляет собой площадь ограниченную кривой 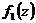, т.е. площадь криволинейной эпюры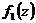

.

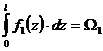Второй интеграл представляет собой статический момент этой площади 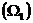относительно 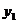, т.е.

,

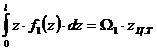где 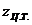— координата центра тяжести первой эпюры.

В результате получим

.

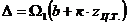Но .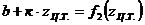

Следовательно 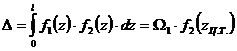. (6.10)

Таким образом, по способу Верещагина операция интегралов заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры взятую под центром тяжести первой. Если обе функции линейные, то операция перемножения обладает свойством коммутативности.

На первый взгляд способ Верещагина не дает существенных упрощений, т.к. его применение требует построения эпюр внутренних усилий от заданной и единичных сил и перемножения их. Однако почти все встречающиеся на практике эпюры внутренних усилий могут быть, как правило, разбиты на три простейшие фигуры: прямоугольник, треугольник и параболу (рис. 6.6).

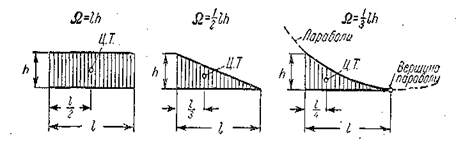
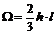
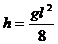
Рис. 6.6

Введение

Под стержневой системой в общем случае понимается любая конструкция, состоящая из элементов имеющих форму бруса. Стержневые системы принято разделять на статически определимые и статически неопределимые. В статически определимых системах все усилия определяются только с помощью уравнений равновесия. В статически неопределимых системах для определения усилий уравнений статики недостаточно.

Основные понятия

Ранее Вы познакомились с расчетами сооружений и их элементов на прочность и жесткость. Однако для суждения надежности конструкции перечисленных расчетов недостаточно, необходимо сжатые элементы на устойчивость. Что же такое устойчивость?

Устойчивость — это старое русское слово. В знаменитом толковом словаре Даля, опубликованного свыше 100 лет назад, слово “устойчивый” означает “стойкий, крепкий, твердый, не шаткий”. В современных словарях оно определяется как “не поддающийся, не подверженный колебаниям и изменениям”.

Понятие устойчивости встречается во всех областях науки и техники. Достаточно назвать устойчивость движения планет, ракет, самолетов, поездов; устойчивость течения воды в реке; устойчивость горения; устойчивость биологического вида, клетки; устойчивость равновесия телебашни, заводской трубы, высотного здания и т.д. Ясно, что в жизни на движущиеся или покоящиеся тела всегда действуют, не учтенные расчетом, малые возмущения, стремящиеся вывести их из этих состояний.

Если малые возмущения вызывают малые отклонения системы от невозмущенного состояния, то невозмущенное состояние является устойчивым.

Таким образом, малые возмущения являются причиной, выводящей систему от невозмущенного состояния. Следствием является ее возврат к первоначальному, либо отклонение от него. И причина и следствие не имеют общей меры и оцениваются в зависимости от обстоятельств.

Пусть имеем многоэтажные здания — близнецы в Москве и Ашхабаде. Поскольку в Москве землетрясений не бывает, то нет опасения за его устойчивость. В сейсмическом районе Ашхабада это здание уже нельзя считать устойчивым, причем одному человеку оно может казаться устойчивым, другому неустойчивым. Для количественного анализа такая оценка совершенно неприемлема. Она нуждается в точном определении, чтобы явление было переложено на язык математического анализа.

Прежде всего, возникает вопрос, что при анализе устойчивости конструкции можно не принимать во внимание и что необходимо учитывать? Короче говоря, как выбрать расчетную схему?

Выбор расчетной схемы зависит от определения понятия устойчивости. Решение большинства задач упругой устойчивости основано на двух простейших понятиях устойчивости Эйлера и Лагранжа. При этом вводятся следующие предпосылки:

1). Геометрическая и силовая схема принимается идеальными (т.е. стержень идеально прямой и идеально упругий, нагрузки приложены в ц.т. сечения).

2). Возмущения, которые налагаются на систему, являются сколь угодно малыми.

Определение устойчивости по Эйлеру:

Равновесие стержня, находящегося под действием продольной силы 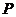, устойчиво по Эйлеру, если после статического приложения и статического снятия возмущающей силы 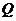, он возвращается к первоначальному положению равновесия.

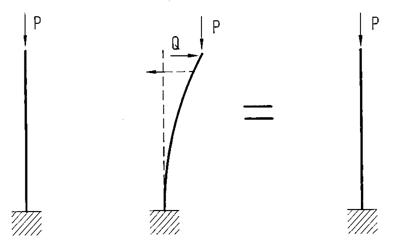
Рис. 8.1

Равновесие стержня, находящегося под действием продольной силы 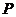, устойчиво по Лагранжу, если после статического приложения возмущающей силы 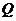и мгновенно ее снятие, стержень после колебаний возвратится к первоначальному положению равновесия.

В математическом смысле понятия устойчивости по Эйлеру — Лагранжу сводится к отысканию нагрузки, при которой происходит бифуркация форм равновесия. Нагрузка, при которой происходит разветвление форм равновесия, называется критической.

При расчете конструкций критическая нагрузка принимается за предельную, по которой и назначается запас устойчивости. Величина запаса устойчивости зависит от условий эксплуатации, а также от степени ответственности конструкции.

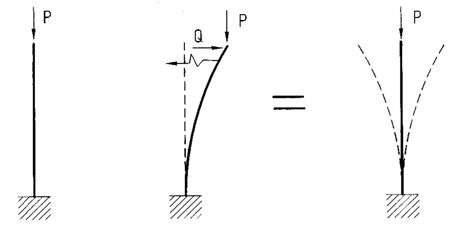
Рис. 8.2

Основные понятия

Совокупность напряжений, возникающих во множестве площадок, проходящих через данную точку, называют напряженным состоянием в точке (или тензором напряжений).

Пусть имеется твердое тело, нагруженное произвольной системой сил (рис. 9.1).

Рис. 9.1

Возьмем произвольную т. 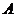вырежем простейшую фигуру — прямоугольный параллелепипед с гранями 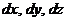. На гранях будут действовать вектора полных напряжений 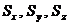каждый из которых может быть разложен на три составляющиеся по осям (рис. 9.2).

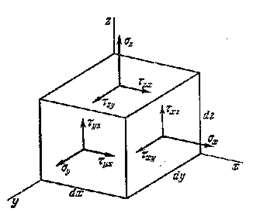
Рис. 9.2

На невидимых гранях действуют такие же напряжения, но противоположно направленные. Этот элемент находится в равновесии, т.к. удовлетворяет уравнение статики

Последние три позволяют получить следующие соотношения — закон парности касательных напряжений.

В силу этого закона из указанных девяти напряжений различны только шесть. Нормальные напряжения считаются положительными, когда они вызывают растяжение элемента. Положительное напряжение компонент касательных напряжений совпадающих с положительным направлением осей, если растягивающие нормальные напряжения для той же грани совпадают с положительным направлением соответствующей оси.

Деформированное состояние

Изменение формы тела связано с перемещением его точек. Расстояние между положением точки до деформации и после деформации 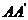называют полным перемещением (Рис. 9.12).

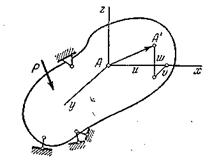
Рис. 9.12

Составляющие вектора полного перемещения по осям обозначим через .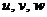

Рассмотрим два ребра параллелепипеда 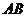и 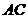. Для простоты на

рис. 9.13 показан отдельно.

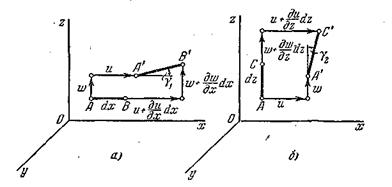
Рис. 9.13

После деформации отрезок 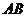занял положение 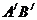. Составляющие вектора перемещений точки 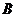отличаются от составляющих вектора перемещений точки 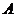на величины, соответствующие координате точки 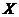. Точка