Глава i. случайные события. вероятность

Глава I. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ

Закономерность и случайность, случайная изменчивость в точных науках, в биологии и медицине

Теория вероятностей – область математики, изучающая закономерности в случайных явлениях. Случайное явление – это явление, которое при неоднократном воспроизведении одного и того же опыта может протекать каждый раз несколько по-иному.

Очевидно, что в природе нет ни одного явления, в котором не присутствовали бы в той или иной мере элементы случайности, но в различных ситуациях мы учитываем их по-разному. Так, в ряде практических задач ими можно пренебречь и рассматривать вместо реального явления его упрощенную схему – «модель», предполагая, что в данных условиях опыта явление протекает вполне определенным образом. При этом выделяются самые главные, решающие факторы, характеризующие явление. Именно такая схема изучения явлений чаще всего применяется в физике, технике, механике; именно так выявляется основная закономерность, свойственная данному явлению и дающая возможность предсказать результат опыта по заданным исходным условиям. А влияние случайных, второстепенных, факторов на результат опыта учитывается здесь случайными ошибками измерений (методику их расчета рассмотрим далее).

Однако описанная классическая схема так называемых точных наук плохо приспособлена для решения многих задач, в которых многочисленные, тесно переплетающиеся между собой случайные факторы играют заметную (часто определяющую) роль. Здесь на первый план выступает случайнаяприродаявления, которой уже нельзя пренебречь. Это явление необходимо изучать именно с точки зрения закономерностей, присущих ему как случайному явлению. В физике примерами таких явлений являются броуновское движение, радиоактивный распад, ряд квантово-механических процессов и др.

Предмет изучения биологов и медиков – живой организм, зарождение, развитие и существование которого определяется очень многими и разнообразными, часто случайными внешними и внутренними факторами. Именно поэтому явления и события живого мира во многом тоже случайны по своей природе.

Элементы неопределенности, сложности, многопричинности, присущие случайным явлениям, обусловливают необходимость создания специальных математических методов для изучения этих явлений. Разработка таких методов, установление специфических закономерностей, свойственных случайным явлениям, –главные задачи теориивероятностей. Характерно, что эти закономерности выполняются лишь при массовости случайных явлений. Причем индивидуальные особенности отдельных случаев как бы взаимно погашаются, а усредненныйрезультатдлямассыслучайных явлений оказывается уже не случайным, а вполнезакономерным.В значительной мере данное обстоятельство явилось причиной широкого распространения вероятностных методов исследования в биологии и медицине.

Рассмотрим основные понятия теории вероятностей.

Виды случайных событий. Основные теоремы теории вероятностей

Все случайные события можно разделить на:

¾ несовместные;

¾ независимые;

¾ зависимые.

Для каждого вида событий характерны свои особенности и теоремы теории вероятностей.

Формула Байеса

Если вероятность совместного появления зависимых событий А и В не зависит от того, в каком порядке они происходят, то Р(А и В) = Р(А) ∙Р(В/А) = Р(В) × Р(А/В). В этом случае условнуювероятность одного из событий можно найти, зная вероятности обоих событий и условную вероятность второго:

Р(В/А) = 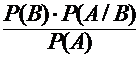(11)

Обобщением данной формулы на случай многих событий является формула Байеса.

Пусть «n» несовместных случайных событий Н₁, Н₂, …, Н_n, образуют полнуюгруппу событий. Вероятности этих событий – Р(Н₁), Р(Н₂), …, Р(Н_n) известны и так как они образуют полную группу , то 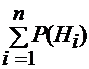= 1.

Некоторое случайное событие А связано с событиями Н₁, Н₂, …, Н_n, причем известны условные вероятности появления события А с каждым из событий Н_i , т.е. известны Р(А/Н₁), Р(А/Н₂), …, Р(А/Н_n). При этом сумма условных вероятностей Р(А/Н_i) может быть не равна единице т.е. 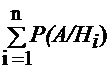≠ 1.

Тогда условная вероятность появления события Н_i при реализации события А (т.е. при условии, что событие А произошло) определяется формулойБайеса:

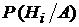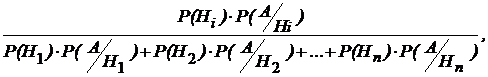= (12)

Причем для этих условных вероятностей .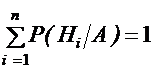

Формула Байеса нашла широкое применение не только в математике, но и в медицине. Например, она используется для вычисления вероятностей тех или иных заболеваний. Так, если Н₁,…, Н_n – предполагаемые диагнозы для данного пациента, А – некоторый признак, имеющий отношение к ним (симптом, определенный показатель анализа крови, мочи, деталь рентгенограммы и т.д.), а условные вероятности Р(А/Н_i) проявления этого признака при каждом диагнозе Н_i (i = 1,2,3,…n) заранее известны, то формула Байеса (12) позволяет вычислить условные вероятности заболеваний (диагнозов) Р(Н_i/А) после того как установлено, что характерный признак А присутствует у пациента.

Пример1. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,5; Р(Н₂) = 0,17; Р(Н₃) = 0,33. Следовательно, предварительно наиболее вероятным кажется первый диагноз. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ (событие А). Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны:

Р(А/Н₁) = 0,1; Р(А/Н₂) = 0,2; Р(А/Н₃) = 0,9.

В полученном анализе зафиксировано увеличение СОЭ (событие А произошло). Тогда расчет по формуле Байеса (12) дает значения вероятностей предполагаемых заболеваний при увеличенном значении СОЭ: Р(Н₁/А) = 0,13; Р(Н₂/А) = 0,09;
Р(Н₃/А) = 0,78. Эти цифры показывают, что с учетом лабораторных данных наиболее реален не первый, а третий диагноз, вероятность которого теперь оказалась достаточно большой.

Приведенный пример – простейшая иллюстрация того, как с помощью формулы Байеса можно формализовать логику врача при постановке диагноза и благодаря этому создать методы компьютерной диагностики.

Пример 2. Определите вероятность, оценивающую степень риска перинатальной* смертности ребенка у женщин с анатомически узким тазом.

Решение: пусть событие Н₁ – благополучные роды. По данным клинических отчетов, Р(Н₁) = 0,975 = 97,5 %, тогда, если Н₂ – факт перинатальной смертности, то Р(Н₂) = 1 – 0,975 = 0,025 = 2,5 %.

Обозначим А – факт наличия узкого таза у роженицы. Из проведенных исследований известны: а) Р(А/Н₁) – вероятность узкого таза при благоприятных родах, Р(А/Н₁) = 0,029, б) Р(А/Н₂) – вероятность узкого таза при перинатальной смертности,
Р(А/Н₂) = 0,051. Тогда искомая вероятность перинатальной смертности при узком тазе у роженицы рассчитывается по формуле Байса (12) и равна:

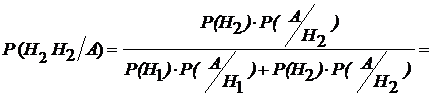
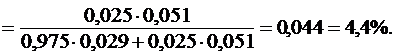
Таким образом, риск перинатальной смертности при анатомически узком тазе значительно выше (почти вдвое) среднего риска (4,4 % против 2,5 %).

Подобные расчеты, обычно выполняемые с помощью компьютера, лежат в основе методов формирования групп пациентов повышенного риска, связанного с наличием того или иного отягощающего фактора.

Формула Байеса очень полезна для оценки многих других медико-биологических ситуаций, что станет очевидным при решении приведенных в пособии задач.

Случайные величины, их виды

В математике величина – это общее название различных количественных характеристик предметов и явлений. Длина, площадь, температура, давление и т.д. – примеры разных величин.

Величина, которая принимает различные числовые значения под влиянием случайных обстоятельств, называется случайной величиной. Примеры случайных величин: число больных на приеме у врача; точные размеры внутренних органов людей и т.д.

Различаютдискретные инепрерывные случайные величины.

Случайная величина называется дискретной, если она принимает только определенные отделенные друг от друга значения, которые можно установить и перечислить.

Примерами дискретной случайной величиной являются:

– число студентов в аудитории – может быть только целым положительным числом: 0,1,2,3,4….. 20…..;

– цифра, которая появляется на верхней грани при бросании игральной кости – может принимать лишь целые значения от 1 до 6;

– относительная частота попадания в цель при 10 выстрелах – ее значения: 0; 0,1; 0,2; 0,3 …1

– число событий, происходящих за одинаковые промежутки времени: частота пульса, число вызовов скорой помощи за час, количество операций в месяц с летальным исходом и т.д.

Случайная величина называется непрерывной, если она может принимать любые значения внутри определенного интервала, который иногда имеет резко выраженные границы, а иногда – нет*. К непрерывным случайным величинам относятся, например, масса тела и рост взрослых людей, масса тела и объем мозга, количественное содержание ферментов у здоровых людей, размеры форменных элементов крови, рН крови и т.п.

Понятие случайной величины играет определяющую роль в современной теории вероятностей, разработавшей специальные приемы перехода от случайных событий к случайным величинам.

Если случайная величина зависит от времени, то можно говорить о случайном процессе.

Глава III

Математические законы теории вероятностей – это математическое выражение реальных закономерностей, которым подчиняются массовые случайные явления. При этом каждое исследование случайных явлений, выполняемое методами теории вероятностей, прямо или косвенно опирается на экспериментальные данные, на результаты испытаний и наблюдений.

Разработка методов получения, описания и анализа экспериментальных данных, определенных в результате исследования массовых случайных явлений, составляет предметспециальной науки – математической статистики.Эти данные принято называть статистическими. Статистические данные часто можно рассматривать как совокупность экспериментальных результатов, которые представляют собой набор возможных значений случайных однородных величин (роста, массы тела, длительности пребывания больного на койке, содержания сахара в крови и т.д.).

Фундаментальными понятиями математической статистики являются генеральная совокупность и выборочная совокупность (выборка). Существуют разные подходы к пониманию смысла этих величин. Мы определяем их так. Генеральная совокупность – это множество подлежащих статистическому изучению однородных объектов, которые характеризуются определенными качественными или количественными признаками. Например, конечная и реально существующая генеральная совокупность – конкретно выбранная популяция: все жители Беларуси в фиксированный момент времени или только все мужчины, или женщины, или дети. Следующий пример: бесконечная и реально существующая генеральная совокупность – множество действительных чисел, лежащих между 0 и 1.

Чтобы изучить генеральную совокупность по какому-либо из ее количественных признаков Х (острота зрения, показатели анализа крови и т.д.), нужно определить закон распределения данного признака и основные характеристики этого распределения, например, математическое ожидание и дисперсию. Для этого следовало бы изучить все ее объекты и затем обработать полученный массив данных методами теории вероятностей. Однако на практике провести сплошное обследование объектов генеральной совокупности часто физически невозможно и экономически невыгодно. Поэтому обычно исследуется только часть объектов, так называемая выборка.

Совокупность «n» объектов, отобранных из интересующей нас генеральной совокупности для конкретного статистического исследования, называется выборочной совокупностью или выборкой.

Исследование выборки дает некоторое приближенное, оценочное значение интересующего нас параметра, принимающего различные значения для разных выборок. Таким образом, постоянная величина – значение нужной характеристики для генеральной совокупности – заменяется значением случайной величины, полученным по результатам выборки на основании некоторого правила. Поэтому главная цель выборочного метода, основного в математической статистике, – повычисленной характеристике выборки как можно точнее определить соответствующую характеристику генеральной совокупности. Это возможно лишь в том случае, когда отобранная для работы часть объектов репрезентативнацелому, т.е. типична, обладает теми же основными чертами, что и все целое. Иначе говоря, выборка должна быть представительной, т.е. по возможности полнее «представлять»свою генеральную совокупность. Это одно из важнейших требований, предъявляемых к выборке, несоблюдение которого ведет к грубым ошибкам и обесценивает результаты исследования. Например, если при изучении заболеваемости населения республики (генеральная совокупность) ишемической болезнью сердца в качестве выборки будет взята группа студентов, то результаты окажутся ошибочны, поскольку свойства выборки не будут соответствовать свойствам генеральной совокупности, как и в случае, когда в качестве выборки будут взяты только пациенты кардиологического диспансера. Репрезентативность выборки обеспечивается ее достаточным объемом и определенными правилами ее формирования, которые в данном пособии не рассматриваются.

Из многочисленных задач, решаемых математической статистикой, выделим следующие.

1. Определение статистических характеристик выборки (методы описательной статистики).

2. Определение параметров генеральной совокупности по данным выборки: точечные оценки и доверительные интервалы для параметров распределения.

3. Исследование статистической связи между двумя признаками выборочной совокупности (элементы корреляционного анализа).

4. Определение значимости различия между двумя выборочными совокупностями (введение в теорию статистических гипотез).

Таблица 4.

Номер интервала
Интервал, масса тела, кг	2,7–2,87	2,87–3,04	3,04–3,21	3,21–3,38	3,38–3,55	3,55–3,72	3,72–3,89	3,89–4,06	4,06–4,23	4,23–4,4
Частота mi
mi/n = pi*	0,04	0,08	0,12	0,16	0,21	0,15	0,11	0,07	0,04	0,02
mi/nh	0,235	0,47	0,7	0,94	1,235	0,88	0,65	0,41	0,235	0,118

Контроль: k=10, 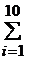m_i =4+8+12+16+21+15+11+7+4+2=100=n (объем выборки),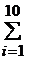 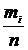= 0,04+0,08+0,12+0,16+0,21+0,15+0,11+0,07+0,04+0,02 = 1.

Обобщим изложенный выше материал.

1. Если выборка исследуется по количественному признаку Х, который представляет собой дискретную случайную величину, то статистическим распределением выборки является вариационным статистический ряд – полученные значения признака, записанные в упорядоченном виде с указанием их частот и относительных частот.

2. Если выборка исследуется по количественному признаку Х, который представляет собой непрерывную случайную величину, то статистическим распределением выборки является интервальный статистический ряд. Он включает в себя интервалы вариант, частоты попадания вариант в эти интервалы, относительные частоты, при необходимости – плотности относительных частот для этих интервалов.

В теории ошибок величину

S = 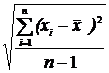(38)

называют средней квадратичной ошибкой прямо измеряемой величины х, величину Dх (см. (36)) – её абсолютной ошибкой, а величину e = 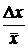× 100 % – относительной ошибкой, оценивающей точность измерений.

При косвенных измеренияхискомую величинуZ вычисляют по некоторой формуле

Z = f(x, y),

где x и y – прямо измеряемые величины.

Число значений x и y, полученных при измерении каждого из них, равно n:

x₁, х₂, х₃, …., х_n ;

у₁, у₂, у₃, … , у_n.

Теперь можно найти их средние арифметические значения:

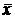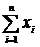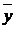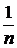
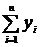= , = (39)

и средние квадратичные ошибки:

S_x = 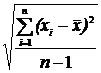; S_у = 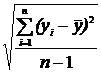, (40)

Среднее арифметическое значение косвенно измеряемой величины вычисляют по формуле

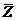= f( 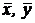). (41)

Истинное значение Z – Z_ист. лежит в доверительном интервале:

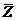– DZ < Z_ист. < 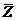+ DZ или Z_ист.= 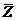± DZ. (3.7.5)

Полуширина данного интервала для нормально распределенной величины Z рассчитывается по формуле:

DZ = t_{g, n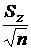} . (43)

В (43) средняя квадратичная ошибка S_z косвенно измеряемой величины, равна:

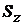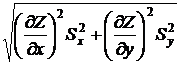= , (44)

где 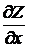=Z_x´ и 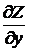=Z_y´ – частные производные величины Z=f(x, y), соответственно, по x и по у, вычисляемые при их средних значениях, S_x и S_у – средние квадртичные ошибки величин х и у, значения которых получаются по формулам (40).

Окончательный результат обычно записывается в виде: Z_ист. = 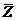± DZ, с указанием выбранного значения g. Приводится так же относительная ошибка косвенно измеряемой величины:

e = 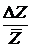× 100 %.

Пример. Рассчитаем случайную ошибку при косвенном измерении вязкости жидкости:

h = h₀ ,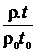

где h, r, t – вязкость, плотность и время истечения исследуемой жидкости из капилляра вискозиметра; h₀, r₀, t₀ – соответственно вязкость, плотность и время истечения эталонной жидкости (воды).

Величины h₀, r₀ и r считаем точно известными, t и t₀ измеряем секундомером, вязкость исследуемой жидкости – косвенно измеряемая величина.

1. Пять измерений времени истечения исследуемой жидкости и воды дали следующие результаты:

для исследуемой жидкости t= 79, 2с;80,4с;78,0с; 83,6с; 80,2 с;

для воды t₀ = 51,0с; 48,4с; 50,6с; 47,4с; 44,2с.

2. Найдем по (39) средние арифметические значения t и t₀:

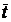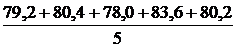= = 80,28 с,

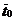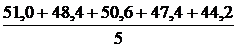= = 48,32 с.

Определим по (41) среднее арифметическое значение вязкости исследуемой жидкости при: r = 790 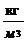, r₀ = 998,2 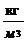, h₀ = 1,0 × 10^-3 Па × с:

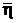= h₀ 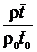; 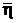= 1,0 × 10^-3 × 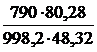= 1,31 × 10^-3 Па× с = 1,31 мПа× с.

3.Рассчитаем среднюю квадратичную ошибку вязкости по (44):

S_h = .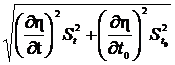

Для этого по (40) определим средние квадратичные ошибки времени истечения исследуемой жидкости S_t и воды :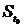

S_t = 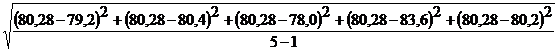=2,09 с

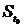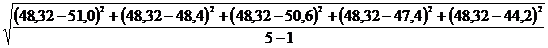= = 2,75 с.

Найдем частные производные 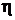при t = 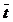и t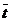₀ = ₀:

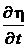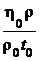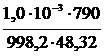= = = 16,38 × 10^-6 Па ,

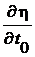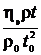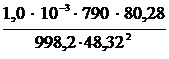= - = – = -27,21 × 10^-6 Па.

Тогда S_h = 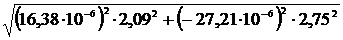= 82,2 × 10^-6 Па × с.

4. Определим полуширину доверительного интервала или абсолютную ошибку вязкости Dh по (43). Для этого, приняв доверительную вероятность g = 0,95, и, зная число измерений непосредственно определяемых величин (n = 5), найдем коэффициент Стьюдента, [cм. табл., напр. в (4, 9)], t_{g, n} = 2,78, тогда:

Dh = 2,78 × = 0,1× 10^-3 Па × с = 0,1 мПа × с.

Следовательно, с доверительной вероятностью g = 0,95 = 95% истинное значение вязкости исследуемой жидкости лежит в интервале

η = 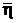± Dh = (1,31 ± 0,1) × 10^-3 Па × с = (1,31 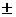0,1) мПа × с.

Относительная ошибка равна

e = 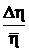× 100 % = 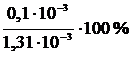» 7,6 %

Глава I. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ