Сущность векторного управления асинхронными двигателями. Аналогии между электроприводом, содержащем АД с векторным управлением, электроприводом с двигателем постоянного тока.

Полное потокосцепление Ψ2 ротора создаётся как токами роторных обмоток, так и токами статорных обмоток. Потокосцепление Ψ2 является векторной величиной и оно вращается в пространстве с частотой ω1 питающего напряжения. Если оси u-v (см. тему 22(4.18-конец)) привязать к вектору потокосцепления Ψ2 ротора так, чтобы ось u совпала с направлением Ψ2, а ось v опережала Ψ2 на 90о, и специальной САР поддерживалось бы постоянство потокосцепления Ψ2=const, то структурная схема АД станет выглядеть подобно структурной схеме ДПТ. Учитывая важность такого результата, оси u-v имеют специальное обозначение - х-у. Управлять АД, представленном в осях х-у, можно точно так же, как управляют ДПТ со всем набором как статических, так и динамических показателей качества. Рассмотренные ранее методы скалярного управления АД обеспечивали лишь статические показатели качества АЭП и совсем не позволяли управлять динамическими показателями качества, которые зависят от переходных процессов в обмотках АД.

Система уравнений (23.6) и выражения-определения потокосцеплений (22.1) после замен в них индексов x←u и y←v и при учете того, что координатные оси х-у, совмещенные с потокосцеплением Ψ2, вращаются с частотой ω1 питающего напряжения (т.е. ωК=ω1), примут вид:

(25.1) (25.2)

Выражение вращающего момента АД возьмем из перечня (23.8) вида:

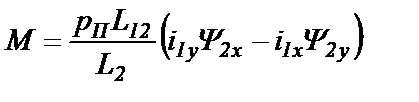(25.3)

Далее будем рассматривать АД с короткозамкнутым ротором. Для этого в описании АД уравнениями (25.1) нужно положить u2x=0 и u2y=0.

Произведем преобразования выражений (25.1…25.3) с учетом Ψ2=const.

Так как вектор потокосцепления Ψ2 направлен по оси х и одновременно перпендикулярен оси у, то проекцией его на ось х будет сам вектор Ψ2, а проекция на ось у будет нулевой (рис.25.1):

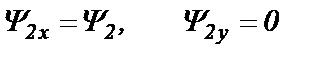(25.4)

Так как специальная САР будет поддерживать постоянство потокосцепления Ψ2, то будет постоянной составляющая Ψ2х, а составляющая Ψ2у будет постоянна всегда, как равная нулю. Производные от постоянных величин будут нулевыми: рΨ2х=0 и рΨ2у=0. Система (25.1) уравнений обмоток АД и выражение (25.3) момента превратятся в

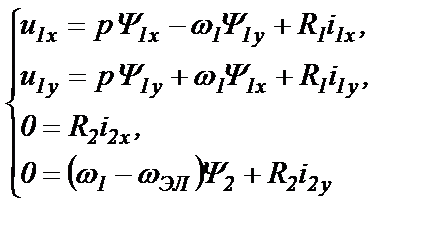(25.5) 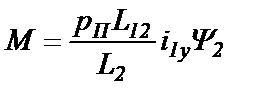(25.6)

Из третьего уравнения системы (25.5) следует: i2х=0. Этот результат используем в упрощениях выражений систем (25.5) и (25.2):

(25.7)

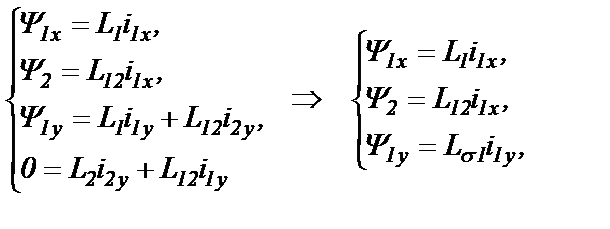(25.8)

где - индуктивное сопротивление рассеяния обмоток статора с учетом шунтирующего действия обмоток ротора через трансформаторную связь между ними.

Введем обозначение механической постоянной . Выражение (25.6) вращающего момента примет вид М=СМ i1y (25.9)

Выражения, входящие в системы (25.7), (25.8) и в (25.9), позволяют установить подобие сигналов в АД и в ДПТ.

Для ДПТ выражение вращающего момента M=СФiЯ=kФФОВiЯ совпадает по структуре с выражением (25.9) для АД, причем потокосцепление Ψ2 является аналогом магнитного потока ФОВ обмотки возбуждения ДПТ, а ток i1у является аналогом тока якоря iЯ ДПТ. Из второго выражения системы (25.8) следует, что током i1х создается потокосцепление Ψ2 и, следовательно, ток i1х является аналогом тока обмотки возбуждения iОВ ДПТ. Следовательно, продольная составляющая i1х тока статора является намагничивающим током, а поперечная i1у – силовым током.

В соответствии с выявленным функциональным назначением токов i1х и i1у составляющая u1х напряжения u1 статора является аналогом напряжения uОВ обмотки возбуждения ДПТ, а составляющая u1у является аналогом напряжения uЯ питания якоря ДПТ.

Отмеченные аналогии сигналов АД и ДПТ отображены в таблице 25.1

Аналогии сигналов ДПТ и АД

Сигнал ДПТ:	uOB	iОВ	ФОВ	uЯ	iЯ	ω	ω0
Сигнал АД:	u1x	i1x	Ψ2	u1у	i1y	ωЭЛ	ω1

Покажем также подобие механических характеристик M=f(ω) ДПТ и АД в осях х-у. Для ДПТ механическая характеристика имеет вид

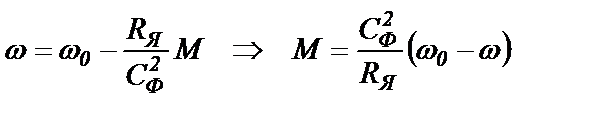(25.10)

Для вывода механической характеристики АД возьмем по одному уравнению из систем (25.7) и (25.8) и преобразуем (25.11)

Подставляем (25.11) в (25.9) и получаем выражение момента АД

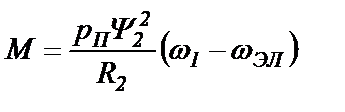(25.12)

Выражения (25.10) и (25.12) механических характеристик ДПТ и АД подобны друг другу.