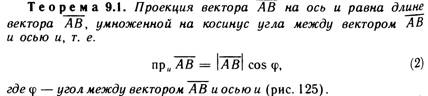Проекция вектора на ось, основные свойства проекций.

Проекция вектора на ось, основные свойства проекций.

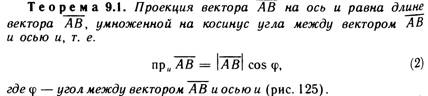
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы.

Для любого вектора 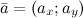, который лежит в плоскости , имеет место следующее разложение:

Если вектор 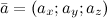расположен в пространстве, то разложение по ортам координатных осей имеет вид: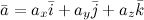

Модуль вектора (длина вектора) в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат

Действия над векторами, заданными проекциями: линейные операции, равенство векторов, коллинеарность векторов.

Два вектора называются равными, если они совмещаются параллельным переносом.
Т.е. существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно.

Доказательство. Пусть AB и CD – одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку A` в точку A, совмещает луч A`B` с лучом AB, потому что они сонаправлены. Отрезка AB и A`B` равны, поэтому точка B совмещается с точкой B`. Значит, параллельный перенос переводит вектор A`B` в вектор AB. Значит векторы равны. Теорема доказана.

Скалярного произведение векторов и его свойства.

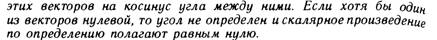
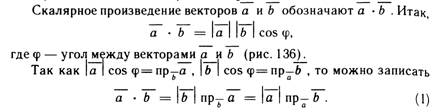
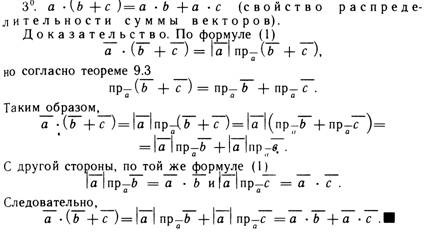
Выражение скалярного произведения через координаты, угол между векторами, проекция вектора на заданное направление.

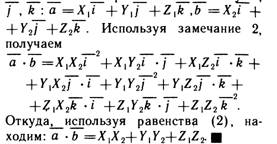
Векторное произведение и его свойства. Выражение векторного произведения через координаты.

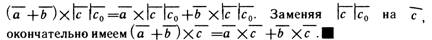
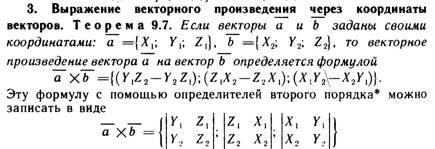
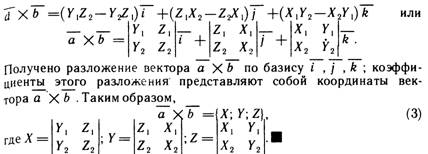
Определение смешанного произведения и его геометрический смысл.

Свойства смешанного произведения. Выражение смешанного произведения через координаты.

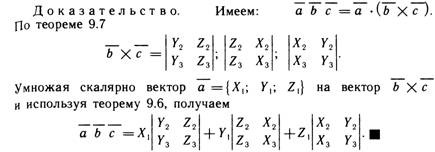
Деление отрезка в данном отношении.

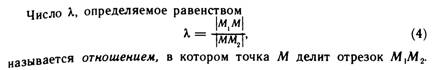
11)Преобразование системы координат, параллельный перенос осей координат.

Поворот осей координат.

Уравнения прямой на плоскости: уравнение прямой с угловым коэффициентом, общее уравнение прямой.

Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две точки.

Уравнение прямой в отрезках. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Пусть дана некоторая точка М₀ и вектор n. Проведем через точку М₀ прямуюl перпендикулярно вектору п (рис. 82).

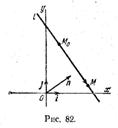
Пусть М — произвольная точка. Точка М лежит на прямой l в том и только в том случае, когда вектор M₀M^> перпендикулярен вектору n, а для этого необходимо и достаточно, чтобы скалярное произведение векторов п и M₀M^> равнялось нулю:

п • M₀M^> = 0. (1)

Чтобы выразить последнее равенство в координатах, введем прямоугольную декартову систему координат. Пусть точки М₀ и М имеют координаты (х₀ ; у₀ ) и (х; у).
Тогда M₀M^> = (х — х₀; у — у₀). Обозначим координаты нормального вектора пчерез (А; В). Теперь равенство (1) можно записать так:

А(х — х₀) + В(у — у₀) = 0. (2)

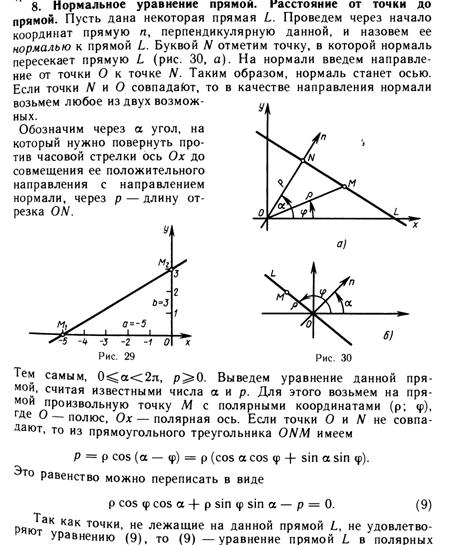
Полярное уравнение прямой. Нормальное уравнение прямой.

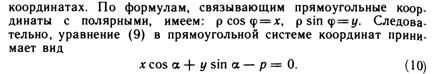
Общие уравнения прямой

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Прямую в пространстве невозможно задать одним уравнением. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой. Для этого требуется система двух или более уравнений.

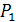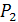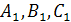Пусть две плоскости и заданы общими уравнениями вида и , т.к. коэффициенты и 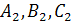не пропорциональны, то плоскости не параллельные. Тогда прямая в пространстве есть пересечение этих плоскостей:

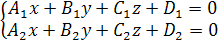
Окружность.

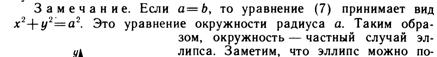
Эллипс.

Преобразовав получаем

Гипербола.

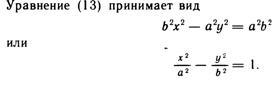
Парабола.

Проекция вектора на ось, основные свойства проекций.