С постоянными коэффициентами.

1)Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
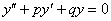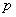, где и 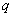– константы (числа), а в правой части – строго ноль.

2)Неоднородное ДУ второго порядка с постоянными коэффициентамиимеет вид:
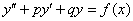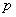, где и 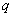– константы, а 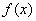– функция, зависящая только от «икс». В простейшем случае функция 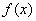может быть числом, отличным от нуля.

Алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

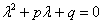
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;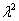
вместо первой производной записываем просто «лямбду»;
вместо функции 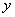ничего не записываем.

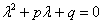– это обычное квадратное уравнение, которое предстоит решить.

Если характеристическое уравнение 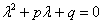имеет два кратных (совпавших) действительных корня 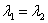(дискриминант 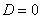), то общее решение однородного уравнения принимает вид:
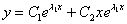, где 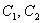– константы.
Если оба корня равны нулю 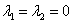, то общее решение опять же упрощается: .

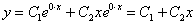Пример ___________________________________________________________

Пример 3

Решить дифференциальное уравнение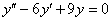

Решение: составим и решим характеристическое уравнение:

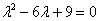
Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно невозбранно применить известную школьную формулу сокращенного умножения:

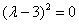
(конечно, формулу нужно увидеть, это приходит с опытом решения)

Получены два кратных действительных корня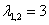

Ответ: общее решение: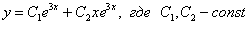

Линейные однородные уравнения высших порядков.

Линейное однородное уравнение третьего порядка имеет следующий вид:
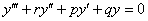, где 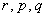– константы.
Для данного уравнения тоже нужно составить характеристическое уравнение и найти его корни. Характеристическое уравнение выглядит так: 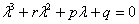, и оно имеет ровно три корня.

Особый случай, когда все три корня кратны (одинаковы). Рассмотрим простейшие однородное ДУ 3-го порядка с одиноким папашей: 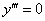. Характеристическое уравнение 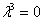имеет три совпавших нулевых корня 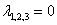. Общее решение записываем так:

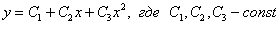
Если характеристическое уравнение 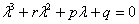имеет, например, три кратных корня 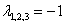, то общее решение, соответственно, такое:

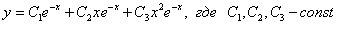
Пример _________________________________________________________

Пример 4 Составим и решим характеристическое уравнение:


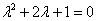
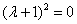
Получены два кратных действительных корня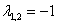
Ответ:общее решение: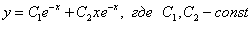

31.Линейные дифференциальные уравнения с постоянными коэффициентами. Случай комплексных корней характеристического уравнения.

Линейные дифференциальные уравнения второго порядка
с постоянными коэффициентами.

1)Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
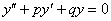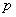, где и 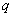– константы (числа), а в правой части – строго ноль.

2)Неоднородное ДУ второго порядка с постоянными коэффициентамиимеет вид:
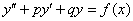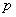, где и 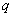– константы, а 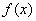– функция, зависящая только от «икс». В простейшем случае функция 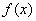может быть числом, отличным от нуля.

Алгоритм решения линейного однородного уравнения второго порядка:

Для того чтобы решить данное ДУ, нужно составить так называемое характеристическое уравнение:

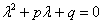
По какому принципу составлено характеристическое уравнение, отчётливо видно:
вместо второй производной записываем ;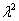
вместо первой производной записываем просто «лямбду»;
вместо функции 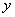ничего не записываем.

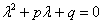– это обычное квадратное уравнение, которое предстоит решить.

Если характеристическое уравнение 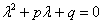имеет сопряженные комплексные корни 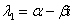, 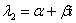(дискриминант 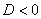), то общее решение однородного уравнения принимает вид:
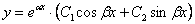, где 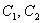– константы.
Примечание: Сопряженные комплексные корни почти всегда записывают кратко следующим образом: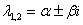

Пример

Решить однородное дифференциальное уравнение второго порядка

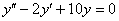
Решение: Составим и решим характеристическое уравнение:


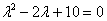
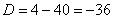
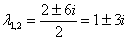– получены сопряженные комплексные корни

Ответ: общее решение: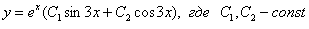

Линейные однородные уравнения высших порядков.

Линейное однородное уравнение третьего порядка имеет следующий вид:
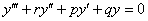, где 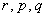– константы.
Для данного уравнения тоже нужно составить характеристическое уравнение и найти его корни. Характеристическое уравнение выглядит так: 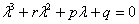, и оно имеет ровно три корня.

Если один корень действительный 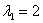, а два других – сопряженные комплексные 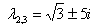, то общее решение записываем так:

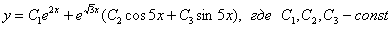
Пример _________________________________________________________

Решить однородное дифференциальное уравнение третьего порядка

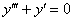
Решение: Составим и решим характеристическое уравнение:

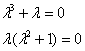
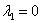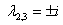, – получен один действительный корень и два сопряженных комплексных корня.

Ответ: общее решение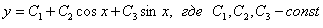

32.Структура частного решения уравнения с постоянными коэффициентами и специальной правой частью.

Линейные однородные дифференциальные уравнения (ЛОДУ) 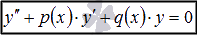и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка .

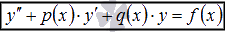Частным случаем дифференциальных уравнений этого вида являются ЛОДУ и ЛНДУ с постоянными коэффициентами.

Общее решение ЛОДУ 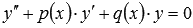на некотором отрезке [a; b]представляется линейной комбинацией двух линейно независимых частных решений y ₁ и y ₂ этого уравнения, то есть, .

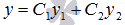Главная сложность заключается именно в нахождении линейно независимых частных решений дифференциального уравнения этого типа. Обычно, частные решения выбираются из следующих систем линейно независимых функций:

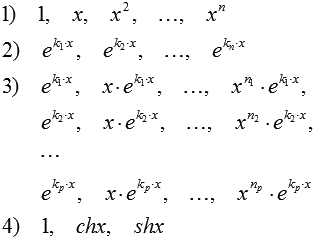
Однако, далеко не всегда частные решения представляются в таком виде.

Примером ЛОДУ является .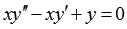

Общее решение ЛНДУ 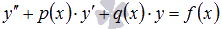ищется в ви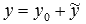де , где 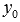- общее решение соответствующего ЛОДУ, а 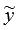- частное решение исходного дифференциального уравнения. О нахождении 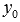мы только что говорили, а 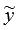можно определить, пользуясь методом вариации произвольных постоянных.

В качестве примера ЛНДУ можно привести .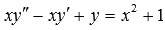

Теорию и решение примеров смотрите в разделе линейные дифференциальные уравнения второго порядка.

33.Метод Фробениуса