Ограничения на структуру исходных данных сняты

Располагая натуральными алгоритмами, можно построить огромное количество различных операций и, значит, огромное количество семейств первичных алгоритмов. Чи­татель помнит, что это связано не только с присоединением к имеющимся операциям новых операций, но и с построе­нием формальных языков, как алгоритмических, так и операндных.

Пользуясь набором натуральных операций, можно по­строить не только операции над словами, но и над другими значительно более сложными конструкциями благодаря операциям линеаризации и делинеаризации. По сравнению с избранными алгоритмами, которые были изучены в логи­ческих теориях, первичные алгоритмы обладают большими возможностями. Вместе с появлением первичных алгорит­мов понятие алгоритма «освобождается от оков», в которых его держали, связывая его с конструктивными объектами, называемыми словами. Объем книги и значительная тру доемкость построения алгоритмов не позволяют автору привести все алгоритмы, которые хотелось бы, для того чтобы проиллюстрировать сказанное. Ограничимся рас­сказом об алгоритмах.

Можно построить натуральные алгоритмы включения и исключения букв перед рассматриваемой буквой преоб­разуемого квазислов. Допустим, что такие алгоритмы у нас уже есть.

…

является алгоритмом выполнения для любого алгоритма ранга r, записью которого является конструкция t.

Если применение алгоритма W к конструкции 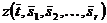дает результат 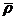, то полагаем, что применение алгоритма t ранга r к набору операндов s₁, s₂, ... , s_r дает тот же результат ρ.

Язык L* называется алгоритмическим языком, а язык L — языком исходных данных. Еще раз подчеркнем, что по существу, таким же образом было введено понятие первичного алгоритма, только вместо алгоритма выполнения там было применено правило выполнения. Мы тогда еще не располагали запасом алгоритмов и потому вынуждены были опираться на правило, в отношении которого не могли сказать, является ли оно алгоритмом, хотя догадывались, что является. В частном случае алгоритм может иметь ранг, равный 1.

Если алгоритм W уже известен, а это всегда так, то можно объявить соответствующую ему операцию. Будем считать, что это сделано, и алгоритмом ранга г называть совокупность записи 1 и операции W.

Иметь дело не с алгоритмом W, а с сопутствующей ему операцией удобнее потому, что, вводя все новые и новые классы алгоритмов с помощью последнего приема, не нужно помнить обо всех «предках» этих алгоритмов.

Вот тут мы допустили еще одно отклонение от схемы определения первичного алгоритма. Вместо правила, вме­сто даже алгоритма выполнения, мы, имея дело с алгорит­мом t, должны знать только операцию . Это не значит, что алгоритм W мы должны забыть ради операции . Нет. Ведь знание алгоритма содержит в себе и знание операции. Какой же смысл в таком отклонении от схемы? Оказы­вается, очень большой. Вместо алгоритма W можно взять любой другой алгоритм, соответствующий той же опера­ции . При этом алгоритм t будет нам так же понятен[25], как ранее при алгоритме W. Для практики очень важно пользоваться самым простым способом запоминания опе­рации W. Сделанное отклонение от схемы дает такую воз­можность. Теперь нетрудно уже дать формулировку ши­рокого формального понятия алгоритма.

Всякий первичный алгоритм, записанный на неко­тором языке L* и работающий над другим языком L, является алгоритмом. Кроме того, всякий r-местный алго­ритм, записанный на некотором языке L* и работающий над языком L,— тоже алгоритм.

Наличие у первичных алгоритмов правил выполнения вместо алгоритма выполнения является их неприятной особенностью. Но эта особенность для практика неощутима. Она неприятна для теоретика. И вот, чтобы ее преодолеть, доказана такая теорема.

Теорема однотипности всех алгорит­мов. Для каждого семейства первичных алгоритмов суще­ствует алгоритм выполнения, графически одинаковый и экви­валентный с их правилом выполнения.

Сам этот алгоритм выполнения принадлежит семейству, находящемуся на достаточно высоком уровне иерархии.

Казалось бы, такая теорема позволяет нам выбросить правила выполнения первичных алгоритмов. Но, увы! Это не так. Если бы мы выбросили все правила выполнения, то система определений понятия алгоритма превратилась бы в порочный круг. А наука (по крайней мере математика) этого не допускает. Несмотря на это, указанная теорема позволяет не выделять первичные алгоритмы из совокуп­ности всех алгоритмов.

Теперь понятие алгоритма достигло высокой степени широты. Алгоритмы приобрели и те две степени свободы, которых им недоставало в предыдущем параграфе. Теперь алгоритмы могут быть какими угодно конструкциями и не только перерабатывать какие угодно конструкции, но и сами они и способы их «действия» могут быть очень разнообраз­ными. Алгоритмы могут не только перерабатывать свои собственные записи, но даже могут «сливаться» с операн­дами, на некотором этапе образуя текст, где невозможно отделить алгоритм от операнда.

Обладая указанными тремя степенями свободы, алго­ритмы становятся пригодными для того, чтобы служить математическими описаниями очень многих реальных объ­ектов и процессов. Перечислим еще раз эти три степени свободы.

1. Для соответствующим образом выбранного алгоритма допустимыми исходными данными могут быть конструкции любого заданного класса конструкций (группирующиеся в формальный язык).

2. Записью алгоритма может быть любая конструкция.

3. В процессе «работы» алгоритмы не только могут пе­рерабатывать исходные данные, но и самих себя и даже «сливаться» е преобразуемыми объектами.

Располагая широким формальным понятием алгоритма мы без существенного труда (только лишь преодолевая не­которые технические трудности) можем доказать, что нор­мальные алгоритмы — это одно из семейств алгоритмов в широком смысле.

То же можно доказать и по отношению к алгоритмам, сопутствующим машинам Тьюринга или рекурсивным функ­циям. Конечно, в данной книге читатель этих доказательств не найдет.