Показательное распределение. Функция надежности

Непрерывная случайная величина X распределена по показательному закону, если ее плотность вероятности имеет вид:

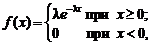(2.33)

где 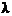– постоянная положительная величина.

График плотности вероятности приведен на рис. 2.9.

Найдем дифференциальную функцию случайной величины X, распределенной по показательному закону. По свойству 2 плотности вероятности:

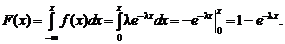
Таким образом,

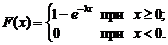(2.34)

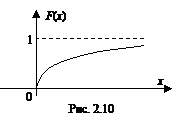График функции распределения показан на рис. 2.10.

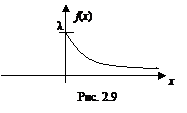Найдем числовые характеристики.

Математическое ожидание:

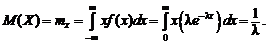
Дисперсия:

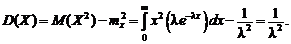
Среднее квадратичное отклонение для показательного распределения:

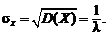
Таким образом:

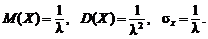
Показательное распределение находит широкое применение в теории надежности, физике, биологии, теории массового обслуживания.

Если рассматривать в качестве непрерывной случайной величины T – длительность безотказной работы элемента, которая, как правило, имеет показательное распределение, тогда интегральная функция:

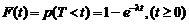(2.35)

определяет вероятность отказа элементов за время t.

Вероятность противоположного события, т.е. вероятность безотказной работы элемента за время t, определяется равенством:

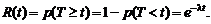
Таким образом:

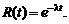(2.36)

Функция (2.36) называется функцией надежности, или показательным законом надежности, где 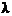выражает интенсивность отказов.

Пример. Время работы лампы имеет показательное распределение. Определить вероятность того, что время безотказной работы радиолампы будет не меньше 600 часов, если среднее время работы радиолампы 400 часов.

Р е ш е н и е. По условию 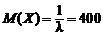, откуда 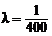и по формуле (2.36):

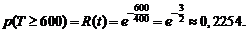
Таким образом, вероятность того, что время безотказной работы радиолампы будет не меньше 600 часов, равна примерно 0,225.

Нормальное распределение

Среди распределений непрерывных случайных величин центральное место занимает нормальный закон (закон Гаусса). Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.

Непрерывная случайная величина X имеет нормальный закон распределения с параметрами a и 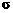, если ее плотность вероятности имеет вид:

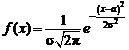. (2.37)

Найдем математическое ожидание и дисперсию нормального распределения. Имеем по формуле (2.19):

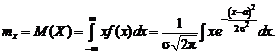
Производя замену переменной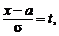

имеем

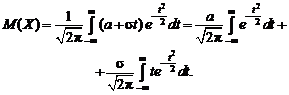
Второй интеграл равен нулю как интеграл от нечетной функции в симметричных пределах, первый интеграл представляет собой известный интеграл Пуассона, который равен 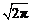. Поэтому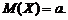

Итак, параметр a является математическим ожиданием случайной величины, имеющей нормальное распределение.

Дисперсия нормального распределения определяется по формуле (2.24):

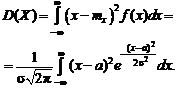
Применив снова замену переменной

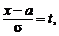
имеем

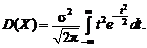
Интегрируя по частям, получим:

.

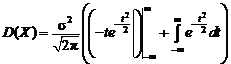Первое слагаемое в скобках равно нулю, так как 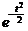при 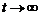убывает быстрее, чем возрастает любая степень t. Второе слагаемое снова есть интеграл Пуассона и, следовательно, равен 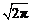. Поэтому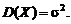

Таким образом, параметр 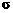в выражении (2.37) есть
среднее квадратичное отклонение случайной величины, имеющей нормальное распределение.

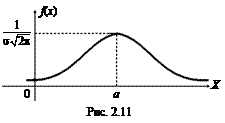
График плотности вероятности нормального распределения (рис. 2.11) называют нормальной кривой (кривой Гаусса).

Нормальное распределение с параметрами 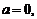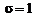называют нормированным распределением.

Отметим некоторые свойства нормальной кривой:

1) кривая симметрична относительно прямой ;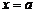

2) при 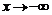ветви кривой асимптотически приближаются к оси OX;

3) точка 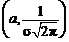является точкой максимума кривой;

4) изменение параметра a при 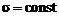приводит к смещению кривой вдоль оси OX;

5) при изменении параметр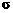а , а 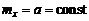кривая изменяет свой вид. При уменьшении 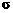кривая распределения становится более крутой.

2.12. Вероятность попадания случайной
величины, имеющей нормальное распределение
на заданный участок. Функции Лапласа

Уже известно, что если непрерывная случайная величина X задана плотностью вероятности 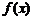, то вероятность попадания X на участок :

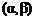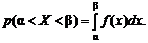
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X принимает значение из интервала :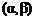

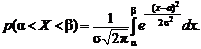
Пользуясь снова заменой переменной

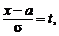
получим:

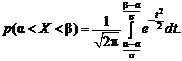(2.38)

Так как интеграл

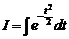
не выражается через элементарные функции, то для вычисления интеграла (2.38) пользуются таблицами значений специальной функции, которая называется функцией Лапласа и имеет вид:

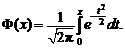(2.39)

Преобразуем выражение (2.38) к функции Лапласа:

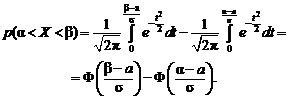
Таким образом,

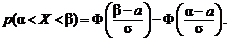(2.40)

Функция Лапласа имеет следующие свойства.

1. Это следует из того, что при 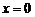пределы интеграла (2.39) совпадают.

2. 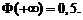Действительно,

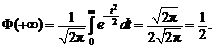
3. Функция Лапласа 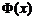есть нечетная функция, т.е.

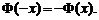
Действительно,

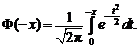
Положив 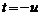, имеем:

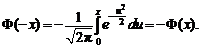
График функции Лапласа изображен на рис. 2.12.

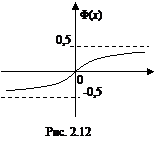Функция распределения случайной величины , распределенной по нормальному закону, выражается через функцию Лапласа 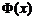по формуле:

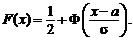
Доказать самостоятельно!

Таблица значений 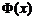приведена в табл. П.2 приложения 6.