Геометрическая вероятность. Задача о встрече

Классическое определение вероятности применимо лишь тогда, когда число всех равновозможных исходов конечно. Однако иногда удается и для бесконечного числа возможных событий использовать принцип «равновозможности», т.е. выделить такую характеристику допустимых случайных событий, которая указывала бы на одинаковые шансы произойти в одном и том же испытании.

Рассмотрим в качестве примера следующее испытание: в некотором квадрате случайным образом выбирается точка. Какова вероятность, что эта точка окажется внутри области D?

Проводя это же испытание для двух разных областей в одном квадрате, естественно, нужно считать, что у случайной точки больше шансов оказаться в той области, у которой вообще «больше» точек, т.е. в области, имеющей большую площадь. Такое понятие «равновозможности» приводит к геометрическому определению вероятности.

Вероятность появления случайной точки внутри некоторой области D определяется как отношение размера этой области к размеру всей области, в которой может появиться данная точка (рис. 1.6).

Для нашего примера:

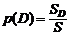, (1.10)

где S_D – площадь области D; S – площадь квадрата; p(D) – вероятность оказаться случайной точке в области D.

В случае одномерной или трехмерной области вместо площади берется длина или объем соответственно.

Таким образом, геометрическая вероятность события – это отношение меры области, благоприятствующей появлению этого события, к мере всей области.

Геометрическое определение вероятности является весьма специфичным. Однако его можно использовать при решении задач с негеометрическим содержанием. Рассмотрим следующую задачу.

Задача о встрече. Два лица A и B условились встретиться в определенном месте между 7 и 8 часами вечера, причем тот, кто приходит первым, ждет другого 20 минут, после уходит. Чему равна вероятность их встречи, если моменты их прихода случайны и независимы друг от друга?

Р е ш е н и е. Обозначим через x и y время прихода A и B в минутах соответственно (после 7 часов вечера). Тогда условие их встречи запишется в виде неравенства:

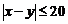. (1.11)

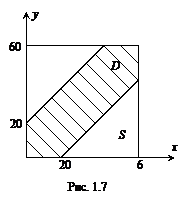Будем рассматривать x и y как координаты на плоскости. Всему рассматриваемому часу будет тогда соответствовать квадрат со сторонами 60. Точками встречи будут все точки заштрихованной области (D) (рис. 1.7), так как только у точек этой области координаты удовлетворяют условию (1.11). Поэтому искомая вероятность (p) может быть вычислена согласно геометрическому определению вероятности (1.10):

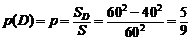
и равна отношению площадей области D и квадрата S.

1.7. Зависимые и независимые события.
Формула умножения вероятностей

Прежде чем рассматривать теорему умножения вероятностей, введем понятия о независимых и зависимых событиях.

Определение 1. Событие A называется независимым по отношению к событию B, если вероятность события A не зависит от того, произошло событие B или нет.

Определение 2. Два события называются независимыми, если появление одного из них не изменит вероятности появления другого.

Определение 3. Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация событий – независимые.

Теорема. Вероятность произведения или совместного наступления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности остальных событий, вычисленные в предположении, что все предшествующие события произошли:

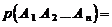
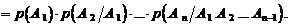(1.12)

Доказательство. Используем метод математической индукции.

Пусть теорема имеет место для 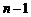событий:

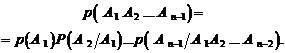
Введем событие 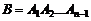. Тогда в силу аксиомы умножения вероятностей

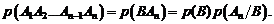
Подставив вместо 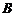, имеем:

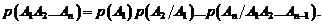
Теорема доказана.

Следствие 1. Если событие A не зависит от события B, то и событие B не зависит от события A.

Следствие 2. Вероятность произведения независимых в совокупности событий равна произведению вероятностей этих событий, т.е. для независимых событий формула (1.12) принимает вид:

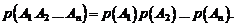(1.13)

Пример 1.В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобрали 3 человека. Найти вероятность того, что все отобранные окажутся мужчинами.

Р е ш е н и е. Введем обозначения событий А₁ – первый мужчина; А₂– второй мужчина; А₃– третий мужчина.

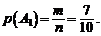
Вероятность того, что второй будет мужчина, при условии, что первым был мужчина, т.е. условная вероятность второго события:

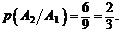
Аналогично:

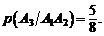
Искомая вероятность равна:

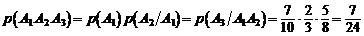
по формуле умножения вероятностей для зависимых событий.

1.8. Теорема сложения вероятностей
для совместных событий

Опыт – бросание игральной кости. Событие А – число выпавших на грани очков равно 6. Событие B – число очков на грани делится на 2. Эти два события совместны.

Теорема 1. Вероятность появления хотя бы одного из двух совместных событий (сумма двух совместных событий) равна сумме вероятностей этих событий без вероятности их совместного появления:

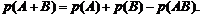(1.14)

Доказательство. Для наступления события 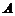достаточно, чтобы произошло хотя бы одно из следующих несовместных событий: АВ или 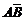, т.е.:

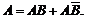
Аналогично для события В:

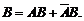
Для наступления хотя бы одного события А или В достаточно, чтобы произошло одно из трех попарно несовместных событий 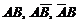, т.е.:

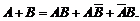
На основании правила сложения вероятностей для несовместных событий имеем:

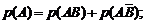(1.15)

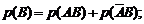(1.16)

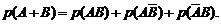(1.17)

Сложив равенства (1.15) и (1.16), получим:

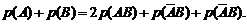
Учитывая равенство (1.17), получим формулу (1.14).

Теорема доказана.

Формула (1.14) имеет простую геометрическую интерпретацию (рис. 1.8).

Рис. 1.8

Если 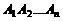– полная группа совместных событий, то формула (1.14) будет громоздкой и в таком случае лучше перейти к противоположному событию, т.е. рассматривать формулу:

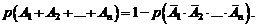(1.18)

Пример. Производится два выстрела по одной и той же мишени. Вероятность попадания при первом выстреле 0,6, а при втором 0,8. Найти вероятность того, что в мишени будет хотя бы одна пробоина.

Р е ш е н и е. Рассмотрим событие A – попадание при первом выстреле, событие B – попадание при втором выстреле. Их вероятности согласно условию равны:

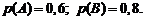
Так как 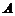и 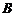являются совместными и независимыми событиями, то вероятность того, что будет хотя бы одна пробоина по формуле (1.14) будет равна:

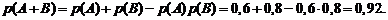
Если же перейти к противоположному событию, то, применяя формулу (1.18) для случая двух событий, получим:

,

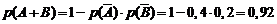при этом учитываем независимость событий A и B.

Формула полной вероятности

Пусть некоторое событие A может наступить или не наступить с одним из ряда несовместных событий: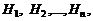
составляющих полную группу. События такого рода называются гипотезами. Вероятности всех гипотез известны, т.е. даны: 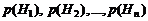, причем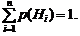

Известны также условные вероятности события A:

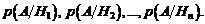
Вероятность события A определяется следующей теоремой.

Теорема. Вероятность появления события A, которое может произойти с одной из гипотез 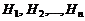, равна сумме парных произведений этих гипотез на отвечающие им условные вероятности наступления события A:

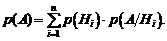(1.19)

Формула (1.19) носит название формулы полной вероятности.

Доказательство. Так как гипотезы 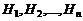образуют полную группу, то событие A можно представить в виде следующей суммы событий:

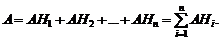
Поскольку 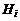– несовместны, то и события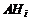 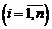также несовместны.

Применяя формулу сложения вероятностей для несовместных событий, имеем:

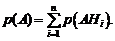(1.20)

Вероятность произведения находим по аксиоме умножения вероятностей (аксиома 5):

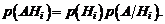
Подставляя полученное выражение в формулу (1.20), получим:

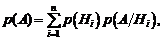
что и требовалось доказать.

Пример. В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры от первого, второго и третьего поставщиков, соответственно, не потребуют ремонта в течение гарантийного срока с вероятностями 98, 88 и 92%. Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.

Р е ш е н и е. Обозначим событие A – телевизор не потребует ремонта в течение гарантийного срока, 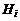– телевизор поступит в торговую фирму от i-го поставщика (i = 1,2,3). По условию:

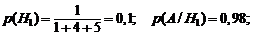
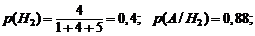
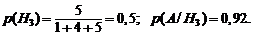
По формуле полной вероятности (1.19):

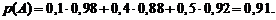
Таким образом, вероятность того, что поступивший в торговую фирму телевизор, не потребует ремонта в течение гарантийного срока, равна 0,91.

Формула Байеса

Поставим теперь следующую задачу. Пусть имеется полная группа несовместных гипотез 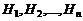. Известны их вероятности:

.

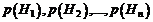Проводится опыт и в результате его осуществляется некоторое событие A, условные вероятности которого известны:

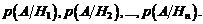
Спрашивается, какие вероятности имеют гипотезы в связи с появлением события 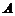. Ответ дает следующая теорема.

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленную на полную вероятность этого события:

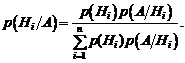(1.21)

Формула (1.21) носит название формулы Байеса.

Доказательство. На основании аксиомы умножения вероятностей имеем:

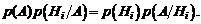
Решая это уравнение относительно 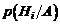при условии, что 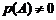, получим:

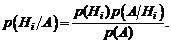
Выражая 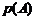с помощью формулы полной вероятности (1.19), получим равенство (1.21).

Значение формулы Байеса состоит в том, что при наступлении события 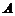, т.е. по мере получения новой информации, можно проверить ее и скорректировать выдвинутые до испытания гипотезы. Такой подход дает возможность корректировать управленческие решения, оценки неизвестных параметров распределения.

Пример. Батарея из трех орудий произвела залп, причем в цель попали два снаряда. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания орудий в цель соответственно равны 0,4; 0,3; 0,5.

Р е ш е н и е. По условию: 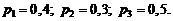Обозначим событие : A – два орудия попали в цель, 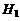– первое орудие попало в цель, 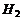– первое орудие не попало в цель, тогда

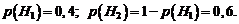
Найдем условную вероятность 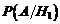, т.е. вероятность того, что в цель попало два снаряда, причем один из них из первого орудия, а следовательно, второй либо из второго, либо из третьего орудия.

Эти события несовместны, поэтому применяем теорему сложения:

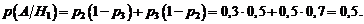
Найдем условную вероятность 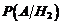, т.е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах, следовательно, попали в цель второе и третье орудия. Эти два события независимы, поэтому применяем формулу умножения:

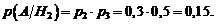
По формуле Байеса (1.21):

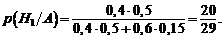
Вероятность попадания первого орудия равна 20/29.

1.11. Последовательность независимых испытаний.
Формула Бернулли

Пусть проводится n независимых испытаний в одинаковых условиях. Вероятность появления некоторого события A в одном отдельном испытании равна p, т.е. .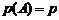

Рассмотрим следующую задачу:

Задача. Найти вероятность того, что в течение указанных n испытаний событие A осуществится ровно k раз .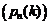

Р е ш е н и е. Обозначим через 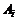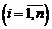наступление события 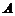в 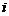-м испытании. В силу постоянства условий испытания:

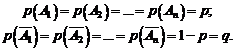
Обозначим через B событие, состоящее в том, что событие A из n испытаний состоится k раз, т.е.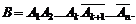

По условию испытания независимы. Это значит, что независимы события, входящие в событие 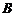. Используя теорему умножения для независимых событий, получим:

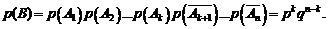
Нами рассмотрена только одна комбинация (один случай). Число всех комбинаций равно числу способов, которыми k появлений события A можно разместить среди всех 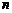испытаний, т.е. числу сочетаний из n элементов по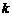 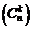. Все эти комбинации событий равновозможные и несовместные. Применяя теорему сложения вероятностей для несовместных событий, получим:

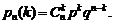(1.22)

Эта формула (1.22) носит название формулы Бернулли.

Формула Бернулли имеет важное значение в теории вероятностей, так как связана с повторением событий в одинаковых условиях, т.е. с такими условиями, в которых как раз и проявляются законы теории вероятностей.

Пример 1. Вероятность изготовления стандартной детали на автоматическом станке равна 0,9. Определить вероятность того, что из 6 наугад взятых деталей 4 окажутся стандартными.

Р е ш е н и е. Условие задачи соответствует схеме повторений испытаний в одинаковых условиях, поэтому, применяя формулу (1.22) при 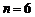, , 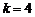, , 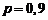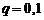получим:

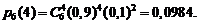
Если же вероятность появления события A в каждом испытании неодинакова, т.е. 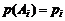, а 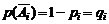, , 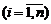то вероятность того, что событие A появится k раз в n испытаниях, равна коэффициенту при 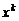в разложении по степеням 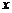производящей функции, имеющей вид:

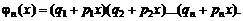(1.23)

Пример 2. Четыре стрелка независимо друг от друга производят по одному выстрелу по общей мишени. Вероятности попадания соответственно равны 0,8; 0,7; 0,6; 0,5. Найти вероятность того, что в мишени будет ровно две пробоины.

Р е ш е н и е. Так как по условию задачи вероятности попадания для стрелков различны:

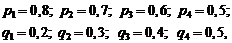
то для решения задачи применим производящую функцию (1.23):

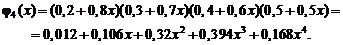
Коэффициент при x² является искомой вероятностью, т.е. .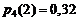

1.12. Наивероятнейшее число наступления события
при повторном испытании

Число наступления события A в n независимых испытаниях называется наивероятнейшим 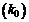, если вероятность наступления k₀ раз события А наибольшая.

Из примера 2 (раздел 1.11) видим, что сначала вероятность возрастает, затем, достигнув 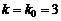, убывает. Выведем формулу для вычисления k₀.

Пусть производится n независимых испытаний и вероятность появления события A в каждом равна p. Тогда по формуле Бернулли наивероятнейшему числу соответствует вероятность: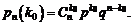

Согласно определению наивероятнейшего числа, вероятность наступления 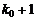и 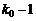раз события A не должна превышать вероятности 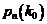, т.е. должны выполняться условия:

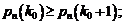(1.24)

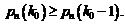(1.25)

На основании формулы (1.24) и формулы Бернулли (1.22) получаем:

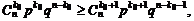
после сокращения

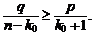
Разрешая это неравенство относительно k₀, имеем:

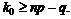(1.26)

Аналогичным образом из неравенства (1.25) имеем:

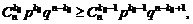
или

.

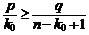Разрешая это неравенство относительно 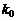, имеем:

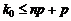. (1.27)

Объединяя неравенства (1.26) и (1.27), получим:

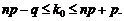(1.28)

Пример. При данном технологическом процессе 85% всей продукции выпускается высшего сорта. Найти наивероятнейшее число изделий высшего сорта из 150 изделий.

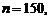
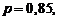
Р е ш е н и е. По условиям примера 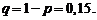Согласно неравенству (1.28) имеем:

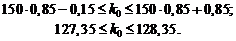
Следовательно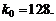

Основные понятия, обозначения и формулы по главе 1 приведены в табл.1.1 и 1.2.

Контрольные вопросы

1. Какие события называют случайными, невозможными, достоверными, равновозможными, совместными, несовместными? Приведите примеры.

2. Какое событие называется противоположным? Приведите примеры.

3. Какие события образуют полную группу несовместных событий? Приведите примеры полных групп событий.

4. Какое событие называется суммой, или объединением, нескольких событий?

5. Какое событие называется произведением, или совмещением, нескольких событий?

6. Что называется частотой события, и каковы ее свойства?

7. Сформулируйте классическое определение вероятности события. В каких пределах изменяется вероятность события?

8. Сформулируйте теорему сложения вероятностей для несовместных событий.

9. Чему равна сумма вероятностей несовместных событий, образующих полную группу?

10. Какая вероятность называется условной?

11. Какие события называются независимыми?

12. Сформулируйте теорему умножения вероятностей и следствия из нее.

13. Как следует вычислять вероятность появления хотя бы одного из нескольких совместных событий?

14. Докажите формулу полной вероятности.

15. Выведите формулу вероятности гипотез (Байеса).

16. Выведите формулу Бернулли. При решении, каких задач применяется формула Бернулли?

17. Какая функция называется производящей функцией вероятности появления события А при n независимых испытаниях? Какой она имеет вид, когда испытания происходят в неодинаковых условиях?

18. Дайте определение наивероятнейшего числа при повторных испытаниях и приведите правило его вычисления.

Таблица 1.1

№ п/п	Событие (обозначение)	Вероятность события р
	Невозможное событие ( )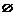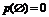
	Элементарное событие ( )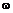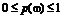
	Достоверное событие ( )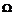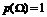
	Равновозможные события (А, В)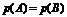
	Противоположное событие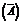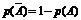
	Сумма совместных событий (А, В)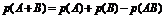
	Сумма несовместных событий (А, В)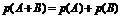
	Произведение зависимых событий (А, В)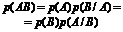
	Произведение независимых событий (А, В)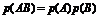
	Сумма полной группы несовместных событий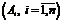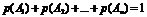

Таблица 1.2

№ п/п	Название формулы	Формула
	Классическая формула вероятности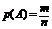
	Сочетание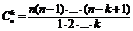
	Размещение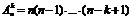
	Перестановки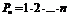
	Сочетания с повторениями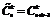
	Размещение с повторениями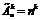
	Перестановки с повторениями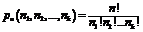
	Геометрическая вероятность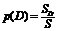
	Формула полной вероятности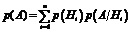
	Формула Байеса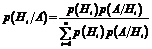
	Формула Бернулли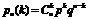
	Производящая формула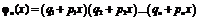
	Наивероятнейшее число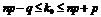

Глава 2. Случайные величины

Понятие случайной величины

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Если событие являлось качественной характеристикой опыта, то случайная величина является количественной характеристикой опыта.

Случайной величиной называется величина, принимающая в результате опыта числовое значение, которое принципиально нельзя предсказать исходя из условий опыта. Примерами случайной величины могут служить:

1. Число дефектных изделий в данной партии.

2. Число попаданий при n выстрелах.

Случайная величина обозначается прописными буквами латинского алфавита 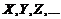, а возможные значения соответственно строчными буквами .

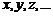Теоретико-множественная трактовка основных понятий теории вероятностей позволяет дать следующее определение случайной величины.

Определение. Случайной величиной X называется действительная функция 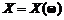, определенная на пространстве элементарных событий 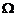, где 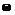– элементарное событие ( 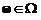), такая, что при любом действительном x событие (X < x) принадлежит алгебре событий.

Чтобы в достаточной степени охарактеризовать случайную величину, нужно прежде всего задать набор ее возможных значений. Эти возможные значения могут быть ограниченными или неограниченными; в зависимости от этого сама случайная величина называется дискретной или непрерывной.

Дискретной случайной величиной называется такая величина, число возможных значений которой конечное либо бесконечное счетное.

Примеры дискретных случайных величин:

1. Число попаданий при трех выстрелах.

Возможные значения случайной величины X, выражающие число попаданий при трех выстрелах, будут x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3.

2. Число вызовов, поступающих на телефонную станцию в течение суток.

Случайная величина в данном примере может принять значения x₁ = 0, x₂ = 1, x₃ = 2…

Непрерывной случайной величиной называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал числовой оси или всю ось, т.е. число возможных значений непрерывной случайной величины бесконечно.

Примеры непрерывных случайных величин:

1) время безотказной работы радиолампы;

2) диаметр отработанной втулки.

2.2. Закон распределения вероятностей
дискретной случайной величины

Рассмотрим дискретную случайную величину X, возможные значения которой x₁, x₂, …, x_n, которые полностью не могут описать случайную величину, так как неизвестно, как часто следует ожидать появление тех или других возможных значений случайной величины.

Для этой цели необходимо знать закон распределения вероятностей случайной величины.

Пусть в результате опыта случайная величина Х примет одно из своих возможных значений, т.е. произойдет одно событие из полной группы несовместных событий: .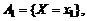

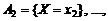
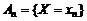Обозначим:

.

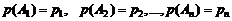Так как события 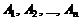образуют полную группу несовместных событий, то .

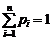Законом распределения дискретной случайной величиныназывается всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Простейшей формулой задания закона распределения является табл. 2.1, которая называется рядом распределения случайной величины.

Таблица 2.1

X	x1	x2	…	xn
p	p1	p2	…	pn

Для наглядности ряд распределения можно представить графически. Графическое изображение ряда распределения называют многоугольником распределения. Ряд распределения можно задать и аналитически, т.е. формулой.

Пример. Монета брошена два раза. Написать закон распределения случайной величины X – числа выпадений герба.

Р е ш е н и е. Дискретная случайная величина X (число выпадений герба) имеет следующие возможные значения: 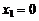(ни разу не выпал герб, т.е. «цц»); 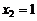(один раз выпал герб, т.е. «гц +цг»); 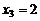(оба раза выпал герб, т.е. «гг»). Вероятности принятия этих возможных значений:

; ;

.

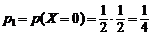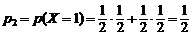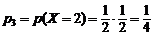Ряд распределения имеет вид:

X
p	0,25	0,5	0,25

.

Контроль: .

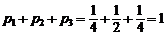Биномиальное распределение

Среди законов распределения для дискретной случайной величины наиболее распространенным является биномиальное распределение, которое имеет место в следующих случаях.

Пусть случайная величина X выражает число появления события A при n независимых испытаниях, проводимых в одинаковых условиях. Вероятность появления события A постоянна и равна p, т.е. p(A) = p. Следовательно, вероятность непоявления события А равна q = 1 – p.

Возможными значениями случайной величины Х будут:

.

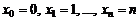Вероятности этих возможных значений определяются по формуле Бернулли:

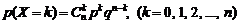. (2.1)

Эта формула является аналитическим заданием закона распределения для данной случайной величины.

Распределение дискретной случайной величины, для которой ряд распределения задается формулой (2.1), называется биномиальным, так как правую часть формулы (2.1) можно рассматривать как общий член разложения бинома Ньютона: (q + p)ⁿ.

Пример. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения отказавших элементов в одном опыте.

Р е ш е н и е. Дискретная случайная величина X (число отказавших элементов в одном опыте) имеет следующие возможные значения:

.

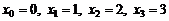Отказы элементов независимы один от другого и вероятности отказа каждого элемента равны между собой, поэтому вероятности принятия возможных значений вычисляем по формуле (2.1), учитывая :

;

;

;

.

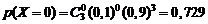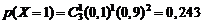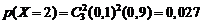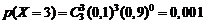Напишем ряд распределения X:

X				. 3
p	0,729	0,243	0,027	0,001

Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1, т.е. сумма вероятностей в ряде распределения равна 1.