Действия над событиями. Алгебра событий

Битнер Г.Г.

Бит 66 Теория вероятностей: Учебное пособие. Ростов-на-Дону: Изд-во Феникс, 2012. 327 с.

ISBN 987-5-7579-1610-1

Излагаемые основы теории вероятностей сопровождаются большим количеством задач, приводимых с решениями. Кроме того, в конце
каждой главы предлагаются вопросы для самопроверки. В приложениях приведены образцы решения двух контрольных заданий и 50 вариантов контрольных заданий, предназначенных для самостоятельной работы студентов очной и заочной форм обучения.

Предназначается для студентов высших учебных заведений, обучающихся по направлениям подготовки и специальностям в области техники и технологии. Будет полезным и для студентов инженерно-экономических факультетов.

УДК 519.2 (07)

ББК 22.171

Табл. 16. Ил. 27. Библиогр.: 22 назв.

Рецензенты:

канд. физ.-мат. наук, доцент А.Б. Будак (Московский
государственный университет им. М.В. Ломоносова);

канд. физ.-мат. наук, доцент А.А. Лобузов (Московский
институт радиотехники, электроники и автоматики)

© Изд-во Феникс, 2012

ISBN 987-5-7579-1610-1 © Г.Г. Битнер, 2012

Предисловие

В основу учебного пособия положены лекции, читаемые автором в течение ряда лет слушателям филиала «Восток» КГТУ
им. А.Н. Туполева. Оно является пособием для студентов инженерно-технических специальностей при изучении вопросов теории вероятностей, элементов теории случайных функций и случайных процессов, предусмотренных программами высших технических учебных заведений.

Учебное пособие включает 6 глав и 6 приложений. В первой главе даны основные понятия теории вероятностей: алгебра событий, классическое и аксиоматическое определение вероятности, формулы комбинаторики, геометрическая вероятность, условные вероятности, формулы сложения и умножения, формулы полной вероятности, Байеса, последовательность независимых испытаний.

Во второй главе рассматриваются случайные величины: функция распределения, ряд распределения дискретной случайной величины, плотность распределения непрерывной случайной величины, математическое ожидание, дисперсия, начальные и центральные моменты, основные дискретные и непрерывные распределения.

Третья глава посвящена системам случайных величин, рассматриваются функция распределения системы двух случайных величин, таблица распределения системы двух дискретных случайных величин, плотность распределения системы двух непрерывных случайных величин, основные числовые характеристики системы двух случайных величин.

В четвертой главе рассматриваются функции случайных величин: построение ряда распределения функции дискретной случайной величины, формулы для плотности распределения одной и двух случайных величин, основные числовые характеристики функций случайных величин.

Пятая глава посвящена закону больших чисел и центральной предельной теореме: рассматриваются неравенство и теорема Чебышева, теорема Бернулли, приведены формулировки теорем Ляпунова и Муавра – Лапласа.

Шестая глава посвящена элементам теории случайных процессов: приводятся понятия, связанные со случайными процессами, выделяются типы случайных процессов, даются некоторые понятия теории массового обслуживания.

В основном тексте пособия много полезных примеров и разобранных задач. Для самопроверки усвоения излагаемого теоретического материала в конце каждой главы приведены подробно составленные контрольные вопросы, а также структурированный в виде таблицы изложенный материал. В приложениях, занимающих бόльшую часть пособия, собран значительный методический материал, полезный для текущего контроля знаний студентов.
В приложениях 1 и 3 приведены образцы решения контрольных заданий, а в приложениях 2 и 4 даны варианты двух контрольных заданий по 50 вариантов в каждом задании, в каждом варианте
8 задач, предназначенных для самостоятельной работы студентов очной и заочной форм обучения. Представленные в контрольных заданиях задачи, разноуровневые как по сложности, так и по целям, позволяют обратить внимание на существенные и принципиальные стороны изучаемых разделов, анализировать теоретические положения, отрабатывать навыки практического решения задач, развивать логическое мышление студентов. Кроме того,
в приложении 5 приведены тесты по 9 темам, позволяющие
проверить качество теоретической и практической подготовки студентов по разделам курса «Теория вероятностей». Все задачи рассчитаны на решение и выбор одного правильного ответа из нескольких предложенных в тексте задачи. Тесты могут быть применены и для компьютерного тестирования на коллоквиумах, зачетах, экзаменах. При составлении учебного пособия была использована литература [1−22].

ВВЕДЕНИЕ

Первые работы, в которых зарождались понятия теории вероятностей, были связаны с исследованиями правил азартных игр. Работы Б. Паскаля, П. Ферма и Х. Гюйгенса в середине XVII в. являлись основой и началом теории вероятностей. Дальнейшее развитие теории вероятностей связано с именами Якоба Бернулли,
А. де Муавра, П.С. Лапласа, К.Ф. Гаусса, С.Д. Пуассона.

В XIX в. вопросами теории вероятностей стали заниматься выдающиеся русские ученые: П.Л. Чебышев, А.А. Марков, А.М. Ляпунов.

Советская школа теории вероятностей занимает в мировой науке ведущее место. Среди многих ученых – виднейших математиков нашей страны, разрабатывающих вопросы теории вероятностей, необходимо отметить С.Н. Бернштейна, А.Я. Хинчина, А.Н. Колмогорова, В.И. Романовского, Б.В. Гнеденко, В.С. Пугачева.

Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, астрономии, геодезии, в общей теории связи. Автоматическое управление производственными процессами, создание автоматических радиолокационных станций и автоматических машин, проблема автоматического управления полетом самолетов и другие технические проблемы автоматики и телемеханики вызвали бурное развитие теории автоматического регулирования, которая не могла обойтись без использования вероятностных методов (особенно теории случайных функций).

Теория вероятностей служит также для обоснования математической и прикладной статистики, которая, в свою очередь, используется при планировании и организации производства, при анализе технологических процессов, при оценке качества продукции и для многих других целей.

Глава 1. Основные понятия
теории вероятностей

Классификация событий

Одним из основных понятий теории вероятностей является понятие события.

Событием называется всякий факт, который может произойти в результате опыта (испытания).

Примером событий могут служить:

1) попадание в цель при выстреле;

2) появление герба при подбрасывании монеты;

3) выход бракованного изделия с конвейера предприятия.

Событие является качественной характеристикой опыта.

Событие принято обозначать заглавными буквами латинского алфавита. Например, событие А – попадание в цель при выстреле, событие B – принятие сигнала радиостанции при наличии помех и т.д.

Событие, которое не может осуществиться при заданном комплексе факторов, называется невозможным и обозначается .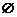

Событие, не содержащее никаких подсобытий кроме невозможного и самого себя, называется элементарными обозначается .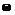

Событие, которое при заданном комплексе факторов обязательно произойдет, называется достоверным и обозначается .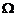

Множество всех элементарных событий называется пространством элементарных событий и является достоверным событием ( ).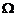

Любое подмножество пространства элементарных событий называется случайным событием (в дальнейшем будем называть просто событием).

События с одинаковыми возможностями осуществления называются равновозможными. Например, выпадение герба или выпадение цифры при подбрасывании монеты. Для проверки этого факта К. Пирсон в первый раз сделал 12 000 бросаний, из них 6 019 раз выпал герб, а во второй раз он сделал 24 000 бросаний, из них 12 012 раз выпал герб.

События называются несовместными, если появление одного из них исключает появление других в одном и том же испытании. Например, подбрасывается монета. Событие A – выпадение герба, событие B – выпадение цифры. A и B – несовместные события.

События называются совместными, если появление одного из них не исключает появление других в одном и том же испытании. Например, подбрасываются две игральные кости. Событие A – выпадение 6 очков на первой кости, событие B – выпадение 6 очков на второй кости. A и B – совместные события.

Два события, одно из которых обязательно должно произойти, но наступление одного события исключает возможность наступления второго, называются противоположными. Событие, противоположное событию A, будем обозначать 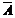. Например, попадание A и промах 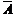при выстреле по цели, работа В и отказ 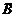при испытании прибора и т.д.

Группа событий A₁, A₂, …, A_n образует полную группу, если в результате испытаний появилось хотя бы одно из них.

Полная группа событий A₁, A₂, …, A_n называется полной группой совместных событий если совместны хотя бы два события из этой группы.

Пример 1. По цели производится три выстрела. Пусть A₁ – попадание при первом выстреле, A₂ – попадание при втором выстреле, A₃ – попадание при третьем выстреле. События A₁, A₂, A₃ образуют полную группу совместных событий.

Полная группа событий A₁, A₂, …, A_n называется полной группой несовместных событий, если события, входящие в группу попарно, несовместны.

Пример 2. По цели производится три выстрела. Пусть A₁ – промах, A₂ – одно попадание, A₃ – два попадания, A₄ – три попадания. События A₁, A₂, A₃, A₄ образуют полную группу несовместных событий.

Формула полной вероятности

Пусть некоторое событие A может наступить или не наступить с одним из ряда несовместных событий: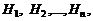
составляющих полную группу. События такого рода называются гипотезами. Вероятности всех гипотез известны, т.е. даны: 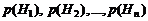, причем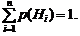

Известны также условные вероятности события A:

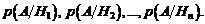
Вероятность события A определяется следующей теоремой.

Теорема. Вероятность появления события A, которое может произойти с одной из гипотез 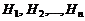, равна сумме парных произведений этих гипотез на отвечающие им условные вероятности наступления события A:

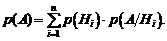(1.19)

Формула (1.19) носит название формулы полной вероятности.

Доказательство. Так как гипотезы 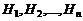образуют полную группу, то событие A можно представить в виде следующей суммы событий:

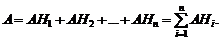
Поскольку 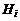– несовместны, то и события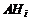 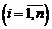также несовместны.

Применяя формулу сложения вероятностей для несовместных событий, имеем:

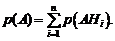(1.20)

Вероятность произведения находим по аксиоме умножения вероятностей (аксиома 5):

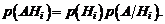
Подставляя полученное выражение в формулу (1.20), получим:

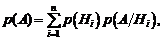
что и требовалось доказать.

Пример. В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры от первого, второго и третьего поставщиков, соответственно, не потребуют ремонта в течение гарантийного срока с вероятностями 98, 88 и 92%. Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.

Р е ш е н и е. Обозначим событие A – телевизор не потребует ремонта в течение гарантийного срока, 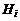– телевизор поступит в торговую фирму от i-го поставщика (i = 1,2,3). По условию:

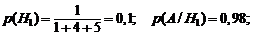
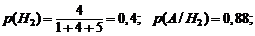
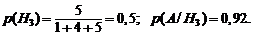
По формуле полной вероятности (1.19):

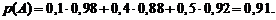
Таким образом, вероятность того, что поступивший в торговую фирму телевизор, не потребует ремонта в течение гарантийного срока, равна 0,91.

Формула Байеса

Поставим теперь следующую задачу. Пусть имеется полная группа несовместных гипотез 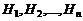. Известны их вероятности:

.

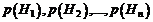Проводится опыт и в результате его осуществляется некоторое событие A, условные вероятности которого известны:

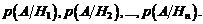
Спрашивается, какие вероятности имеют гипотезы в связи с появлением события 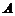. Ответ дает следующая теорема.

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленную на полную вероятность этого события:

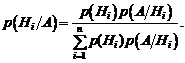(1.21)

Формула (1.21) носит название формулы Байеса.

Доказательство. На основании аксиомы умножения вероятностей имеем:

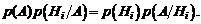
Решая это уравнение относительно 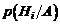при условии, что 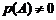, получим:

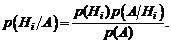
Выражая 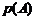с помощью формулы полной вероятности (1.19), получим равенство (1.21).

Значение формулы Байеса состоит в том, что при наступлении события 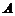, т.е. по мере получения новой информации, можно проверить ее и скорректировать выдвинутые до испытания гипотезы. Такой подход дает возможность корректировать управленческие решения, оценки неизвестных параметров распределения.

Пример. Батарея из трех орудий произвела залп, причем в цель попали два снаряда. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания орудий в цель соответственно равны 0,4; 0,3; 0,5.

Р е ш е н и е. По условию: 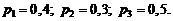Обозначим событие : A – два орудия попали в цель, 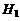– первое орудие попало в цель, 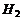– первое орудие не попало в цель, тогда

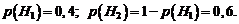
Найдем условную вероятность 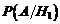, т.е. вероятность того, что в цель попало два снаряда, причем один из них из первого орудия, а следовательно, второй либо из второго, либо из третьего орудия.

Эти события несовместны, поэтому применяем теорему сложения:

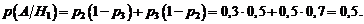
Найдем условную вероятность 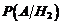, т.е. вероятность того, что в цель попало два снаряда, причем первое орудие дало промах, следовательно, попали в цель второе и третье орудия. Эти два события независимы, поэтому применяем формулу умножения:

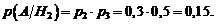
По формуле Байеса (1.21):

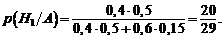
Вероятность попадания первого орудия равна 20/29.

1.11. Последовательность независимых испытаний.
Формула Бернулли

Пусть проводится n независимых испытаний в одинаковых условиях. Вероятность появления некоторого события A в одном отдельном испытании равна p, т.е. .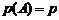

Рассмотрим следующую задачу:

Задача. Найти вероятность того, что в течение указанных n испытаний событие A осуществится ровно k раз .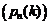

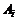
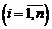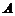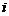Р е ш е н и е. Обозначим через наступление события в -м испытании. В силу постоянства условий испытания:

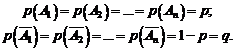
Обозначим через B событие, состоящее в том, что событие A из n испытаний состоится k раз, т.е.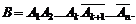

По условию испытания независимы. Это значит, что независимы события, входящие в событие 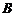. Используя теорему умножения для независимых событий, получим:

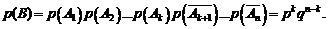
Нами рассмотрена только одна комбинация (один случай). Число всех комбинаций равно числу способов, которыми k появлений события A можно разместить среди всех 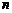испытаний, т.е. числу сочетаний из n элементов по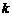 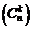. Все эти комбинации событий равновозможные и несовместные. Применяя теорему сложения вероятностей для несовместных событий, получим:

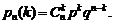(1.22)

Эта формула (1.22) носит название формулы Бернулли.

Формула Бернулли имеет важное значение в теории вероятностей, так как связана с повторением событий в одинаковых условиях, т.е. с такими условиями, в которых как раз и проявляются законы теории вероятностей.

Пример 1. Вероятность изготовления стандартной детали на автоматическом станке равна 0,9. Определить вероятность того, что из 6 наугад взятых деталей 4 окажутся стандартными.

Р е ш е н и е. Условие задачи соответствует схеме повторений испытаний в одинаковых условиях, поэтому, применяя формулу (1.22) при 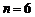, , 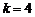, , 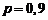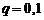получим:

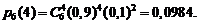
Если же вероятность появления события A в каждом испытании неодинакова, т.е. 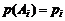, а 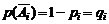, , 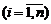то вероятность того, что событие A появится k раз в n испытаниях, равна коэффициенту при 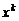в разложении по степеням 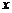производящей функции, имеющей вид:

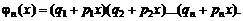(1.23)

Пример 2. Четыре стрелка независимо друг от друга производят по одному выстрелу по общей мишени. Вероятности попадания соответственно равны 0,8; 0,7; 0,6; 0,5. Найти вероятность того, что в мишени будет ровно две пробоины.

Р е ш е н и е. Так как по условию задачи вероятности попадания для стрелков различны:

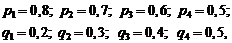
то для решения задачи применим производящую функцию (1.23):

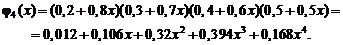
Коэффициент при x² является искомой вероятностью, т.е. .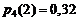

1.12. Наивероятнейшее число наступления события
при повторном испытании

Число наступления события A в n независимых испытаниях называется наивероятнейшим 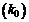, если вероятность наступления k₀ раз события А наибольшая.

Из примера 2 (раздел 1.11) видим, что сначала вероятность возрастает, затем, достигнув 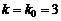, убывает. Выведем формулу для вычисления k₀.

Пусть производится n независимых испытаний и вероятность появления события A в каждом равна p. Тогда по формуле Бернулли наивероятнейшему числу соответствует вероятность: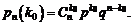

Согласно определению наивероятнейшего числа, вероятность наступления 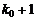и 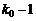раз события A не должна превышать вероятности 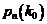, т.е. должны выполняться условия:

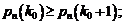(1.24)

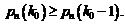(1.25)

На основании формулы (1.24) и формулы Бернулли (1.22) получаем:

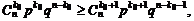
после сокращения

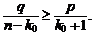
Разрешая это неравенство относительно k₀, имеем:

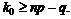(1.26)

Аналогичным образом из неравенства (1.25) имеем:

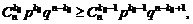
или

.

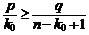Разрешая это неравенство относительно 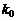, имеем:

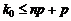. (1.27)

Объединяя неравенства (1.26) и (1.27), получим:

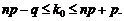(1.28)

Пример. При данном технологическом процессе 85% всей продукции выпускается высшего сорта. Найти наивероятнейшее число изделий высшего сорта из 150 изделий.

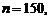
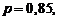
Р е ш е н и е. По условиям примера 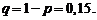Согласно неравенству (1.28) имеем:

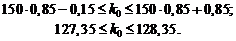
Следовательно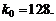

Основные понятия, обозначения и формулы по главе 1 приведены в табл.1.1 и 1.2.

Контрольные вопросы

1. Какие события называют случайными, невозможными, достоверными, равновозможными, совместными, несовместными? Приведите примеры.

2. Какое событие называется противоположным? Приведите примеры.

3. Какие события образуют полную группу несовместных событий? Приведите примеры полных групп событий.

4. Какое событие называется суммой, или объединением, нескольких событий?

5. Какое событие называется произведением, или совмещением, нескольких событий?

6. Что называется частотой события, и каковы ее свойства?

7. Сформулируйте классическое определение вероятности события. В каких пределах изменяется вероятность события?

8. Сформулируйте теорему сложения вероятностей для несовместных событий.

9. Чему равна сумма вероятностей несовместных событий, образующих полную группу?

10. Какая вероятность называется условной?

11. Какие события называются независимыми?

12. Сформулируйте теорему умножения вероятностей и следствия из нее.

13. Как следует вычислять вероятность появления хотя бы одного из нескольких совместных событий?

14. Докажите формулу полной вероятности.

15. Выведите формулу вероятности гипотез (Байеса).

16. Выведите формулу Бернулли. При решении, каких задач применяется формула Бернулли?

17. Какая функция называется производящей функцией вероятности появления события А при n независимых испытаниях? Какой она имеет вид, когда испытания происходят в неодинаковых условиях?

18. Дайте определение наивероятнейшего числа при повторных испытаниях и приведите правило его вычисления.

Таблица 1.1

№ п/п	Событие (обозначение)	Вероятность события р
	Невозможное событие ( )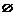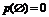
	Элементарное событие ( )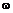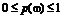
	Достоверное событие ( )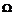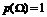
	Равновозможные события (А, В)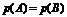
	Противоположное событие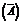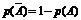
	Сумма совместных событий (А, В)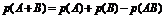
	Сумма несовместных событий (А, В)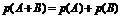
	Произведение зависимых событий (А, В)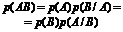
	Произведение независимых событий (А, В)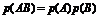
	Сумма полной группы несовместных событий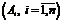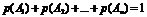

Таблица 1.2

№ п/п	Название формулы	Формула
	Классическая формула вероятности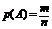
	Сочетание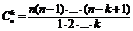
	Размещение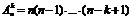
	Перестановки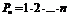
	Сочетания с повторениями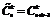
	Размещение с повторениями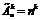
	Перестановки с повторениями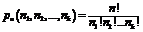
	Геометрическая вероятность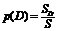
	Формула полной вероятности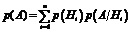
	Формула Байеса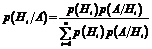
	Формула Бернулли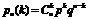
	Производящая формула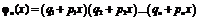
	Наивероятнейшее число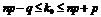

Глава 2. Случайные величины

Понятие случайной величины

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Если событие являлось качественной характеристикой опыта, то случайная величина является количественной характеристикой опыта.

Случайной величиной называется величина, принимающая в результате опыта числовое значение, которое принципиально нельзя предсказать исходя из условий опыта. Примерами случайной величины могут служить:

1. Число дефектных изделий в данной партии.

2. Число попаданий при n выстрелах.

Случайная величина обозначается прописными буквами латинского алфавита 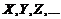, а возможные значения соответственно строчными буквами .

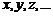Теоретико-множественная трактовка основных понятий теории вероятностей позволяет дать следующее определение случайной величины.

Определение. Случайной величиной X называется действительная функция 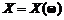, определенная на пространстве элементарных событий 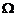, где 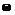– элементарное событие ( 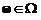), такая, что при любом действительном x событие (X < x) принадлежит алгебре событий.

Чтобы в достаточной степени охарактеризовать случайную величину, нужно прежде всего задать набор ее возможных значений. Эти возможные значения могут быть ограниченными или неограниченными; в зависимости от этого сама случайная величина называется дискретной или непрерывной.

Дискретной случайной величиной называется такая величина, число возможных значений которой конечное либо бесконечное счетное.

Примеры дискретных случайных величин:

1. Число попаданий при трех выстрелах.

Возможные значения случайной величины X, выражающие число попаданий при трех выстрелах, будут x₁ = 0, x₂ = 1, x₃ = 2, x₄ = 3.

2. Число вызовов, поступающих на телефонную станцию в течение суток.

Случайная величина в данном примере может принять значения x₁ = 0, x₂ = 1, x₃ = 2…

Непрерывной случайной величиной называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал числовой оси или всю ось, т.е. число возможных значений непрерывной случайной величины бесконечно.

Примеры непрерывных случайных величин:

1) время безотказной работы радиолампы;

2) диаметр отработанной втулки.

2.2. Закон распределения вероятностей
дискретной случайной величины

Рассмотрим дискретную случайную величину X, возможные значения которой x₁, x₂, …, x_n, которые полностью не могут описать случайную величину, так как неизвестно, как часто следует ожидать появление тех или других возможных значений случайной величины.

Для этой цели необходимо знать закон распределения вероятностей случайной величины.

Пусть в результате опыта случайная величина Х примет одно из своих возможных значений, т.е. произойдет одно событие из полной группы несовместных событий: .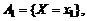

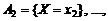
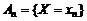Обозначим:

.

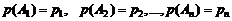Так как события 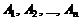образуют полную группу несовместных событий, то .

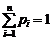Законом распределения дискретной случайной величиныназывается всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Простейшей формулой задания закона распределения является табл. 2.1, которая называется рядом распределения случайной величины.

Таблица 2.1

X	x1	x2	…	xn
p	p1	p2	…	pn

Для наглядности ряд распределения можно представить графически. Графическое изображение ряда распределения называют многоугольником распределения. Ряд распределения можно задать и аналитически, т.е. формулой.

Пример. Монета брошена два раза. Написать закон распределения случайной величины X – числа выпадений герба.

Р е ш е н и е. Дискретная случайная величина X (число выпадений герба) имеет следующие возможные значения: 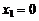(ни разу не выпал герб, т.е. «цц»); 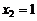(один раз выпал герб, т.е. «гц +цг»); 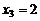(оба раза выпал герб, т.е. «гг»). Вероятности принятия этих возможных значений:

; ;

.

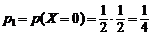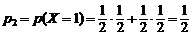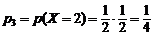Ряд распределения имеет вид:

X
p	0,25	0,5	0,25

.

Контроль: .

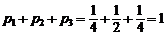Биномиальное распределение

Среди законов распределения для дискретной случайной величины наиболее распространенным является биномиальное распределение, которое имеет место в следующих случаях.

Пусть случайная величина X выражает число появления события A при n независимых испытаниях, проводимых в одинаковых условиях. Вероятность появления события A постоянна и равна p, т.е. p(A) = p. Следовательно, вероятность непоявления события А равна q = 1 – p.

Возможными значениями случайной величины Х будут:

.

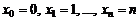Вероятности этих возможных значений определяются по формуле Бернулли:

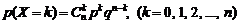. (2.1)

Эта формула является аналитическим заданием закона распределения для данной случайной величины.

Распределение дискретной случайной величины, для которой ряд распределения задается формулой (2.1), называется биномиальным, так как правую часть формулы (2.1) можно рассматривать как общий член разложения бинома Ньютона: (q + p)ⁿ.

Пример. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения отказавших элементов в одном опыте.

Р е ш е н и е. Дискретная случайная величина X (число отказавших элементов в одном опыте) имеет следующие возможные значения:

.

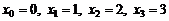Отказы элементов независимы один от другого и вероятности отказа каждого элемента равны между собой, поэтому вероятности принятия возможных значений вычисляем по формуле (2.1), учитывая :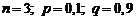

;

;

;

.

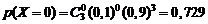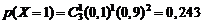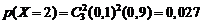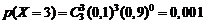Напишем ряд распределения X:

X				. 3
p	0,729	0,243	0,027	0,001

Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1, т.е. сумма вероятностей в ряде распределения равна 1.

Равномерное распределение

Непрерывная случайная величина X имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его – равна нулю, т.е.

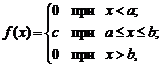(2.30)

где .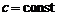

Найдем с из свойства 4 плотности распределения:

.

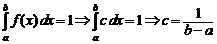Итак, плотность распределения

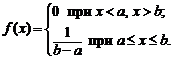(2.31)

График 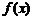показан на рис. 2.7.

Найдем функцию распределения 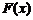для равномерного распределени<