Дискретная случайная величина

Для заданной дискретной случайной величины Х :

а) построить ряд распределения;

б) записать и построить функцию распределения F(x);

в) найти характеристики: математическое ожидание (т);

дисперсию (D), среднее квадратичное отклонение (S), моду, коэффициент вариации, коэффициент асимметрии, эксцесс;

N61.

Имеется n-лампочек; каждая из них с вероятностью р имеет дефект. Лампочка ввинчивается в патрон и включается ток; при включении тока дефектная лампочка сразу же перегорает, после чего заменяется другой. Е - случайная величина числа лампочек, которое будет испробовано.

N62.

Два баскетболиста поочередно забрасывают мяч в корзину до тех пор, пока один из них не попадет. Е - случайное число бросков, производимых каждым из баскетболистов, если вероятность попадания первого равна 0.4, а второго0.6.

N63.

Мишень состоит из круга 1 и двух концентрических колец с номерами 2 и 3. Попадание в круг 1 дает 10 очков, в кольцо 2 дает 5 очков, а в кольцо 3 - 1 очко. Вероятности попадания в круг 1 и в кольца 2 и 3 соответственно равны 0.5, 0.3, 0.2. Е - случайная сумма выбитых очков в результате трех выстрелов.

N64.

Производятся испытания n изделий на надежность, причем вероятность выдержать испытание для каждого изделия равна р. Е -случайное число изделий, выдержавших испытание.

N65.

Имеется n заготовок для одной и той же детали. Вероятность изготовления годной детали из каждой заготовки равна р. Е -случайное число используемых заготовок.

N66.

В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Е - число нестандартных деталей среди 2 отобранных.

N67.

Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна0.9. В каждой партии содержится 5 изделий. Е - число партий, в каждой из

которых окажется ровно 4 стандартных изделия, если проверке подлежат 50 партий.

N68.

Имеется 6 ключей, из которых только один подходит к замку. Е -число попыток при открывании замка, если испробованный ключ в последующих открываниях не участвует.

N69.

Батарея состоит из 3-х орудий. Вероятность попадания в цель при одном выстреле из первого, второго и третьего орудия батареи равна соответственно: 0.5, 0.6 и 0.8. каждое из орудий стреляет по некоторой цели один раз. Е - число попаданий в мишень.

N70.

Производится набрасывание колец на колышек до первого попадания (либо до полного израсходования колец). Число колец равно пяти. Е - число брошенных колец, если вероятность попадания 0.9.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА

Для заданной непрерывной случайной величины Х :

а) записать и построить функцию плотности f(x);

б) записать и построить функцию распределения F(x);

в) проверить выполнение свойств f(x) и F(x);

г) найти характеристики: математическое ожидание (т);

дисперсию (D), среднее квадратичное отклонение (S), моду, медиану, коэффициент вариации, коэффициент асимметрии, эксцесс;

д) найти p(|X-m|<S) и p(|X-m|<3S). На график f(x) нанести m и интервалы, указанные в д).

N71.

х + а, х є (0;1);

f(x)= 0, иначе, а - ?

N72.

ax², 0<=x<=l;

f(x)= 0, иначе, а -?

N73.

a cos х, 0 < x < П/2;

f(x)= 0, иначе, а- ?

N74.

(sin x )/ a, x є (0; П);

f(x)= 0, иначе, а- ?

N75.

2a - 3x, 0 <=x<5;

f(x)= 0, иначе, а - ?

N76.

(a cos² x)/3, x е (-П/2;П/2);

f(x)= 0, иначе, а -?

N77.

b x² , x є (0;3);

f(x)= 0, иначе, b- ?

N78.

с х³, х є (0;1);

f(x)= 0, иначе, с - ?

N79.

x² + ax, x є (0;1);

f(x)= 0, иначе, а - ?

N80.

x² + a, x є (0;2);

f(x)= 0, иначе, а - ?

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.

N81.

Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина) 50 мм. Фактически, длина изготовленных деталей не менее 32мм и не более 68 мм. Найти вероятность того, что длина случайно отобранной детали будет меньше 40 мм; больше 55 мм.

N82.

Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 8=10мм. Найти вероятность того, что при двух измерениях ошибка ни в одном не превзойдет15 мм.

N83.

Случайная величина Х имеет нормальное распределение с математическим ожиданием М=25. Вероятность попадания Х в интервал(10,15) равна 0.2. Чему равна вероятность попадания Х в интервал(35,40)?

N84.

Случайные ошибки измерения подчинены нормальному закону с математическим ожиданием 0 и средним квадратичным отклонением 10 мм. Найти вероятность того, что при3-х независимых измерениях ошибка хотя бы одного не превзойдет 10 мм?

N85.

Случайная величина Х имеет нормальное распределение с математическим ожиданием М=10. Вероятность попадания Х в интервал (0,20) равна 0.9973. Чему равна вероятность попадания Х в интервал (0,5)?

N86.

Случайная величина Х имеет нормальное распределение N(0,1). Что больше: вероятность попадания Х в интервал (-0.5,-0.1) или в интервал (1,2)?

N87.

Случайная величина Х имеет нормальное распределение N(0,1). Что больше: вероятность /Х/>0.7 или /Х/<0.3?

N88.

Случайная величина Х имеет нормальное распределение N(1,1). Что больше: вероятность попадания Х в интервал (-1,0) или в интервал (0,0.5)?

N89.

Случайная величина Х имеет нормальное распределение с математическим ожиданием М=0. Вероятность попадания Х в интервал (0,2) равна 0.9. Чему равна вероятность попадания Х в

интервал (0,1)?

N90.

В нормально распределенной совокупности 25% значений Х меньше 0 и 40% значений Х больше 2. Найти среднее значение и стандартное отклонение данного распределения.

Задание№4

В вариантах № 1 – 30 приведены результаты n = 50 наблюдений за парой признаков (X, Y). В задании необходимо выполнить в 1-ую очередь задачи № 1 – 5 и 9 – 11; затем три оставшихся, то есть № 6 – 8.

1. Составить корреляционную Таблицу, содержащую два входа, по числу признаков, пояснить ее устройство;

2. Построить вариационный ряд для признака X или Y (задано в данных варианта);

3. Найти числовые характеристики заданого признака (X или Y): методом произведений вычислить выборочное среднее, выборочную дисперсию, D_в, выборочное среднее квадратическое отклонение 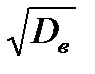, и определить для выбранного признака исправленную дисперсию, S², и “исправленное” среднее квадратическое отклонение 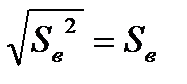, существенна ли поправка?

4. Найти другие характеристики вариационного ряда для признака X или Y: Моду М_о, Медиану m_e, Размах варьирования R, Среднее абсолютное отклонение θ, Коэффициент вариации V.

5. Построить полигон частот и найти эмпирическую функцию распределения для заданого признака (X или Y);

6. Предполагая, что заданый признак (X или Y) распределен в генеральной совокупности по нормальному закону, найти с надежностью γ (γ – задано) доверительный интервал для оценки неизвестного математического ожидания а в генеральной сово­купности при неизвестном σ (среднем квадратическом отклонении);

7. Предполагая, что заданый признак (X или Y) распределен в генеральной совокупности по нормальному закону, найти с надежностью γ (γ – задано) доверительный интервал для оценки среднего квадратического отклонения σ;

8. Найти методом наибольшего правдоподобия оценки параметров а и σ для нормально распределенного заданного признака, является ли оценка для σ несмещенной?

9. Найти выборочный коэффициент корреляции между признаками Y и X;

10. Найти уравнение линейной регрессии 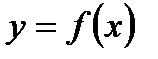и дать объяснение полученного результата, объяснить смысл найденного коэффициента корреляции;

11.Построить корреляционное поле по корреляционной Таблице и нанести график найденной прямой регрессии на корреляционное поле, нанести на этот же график соответствующие условные вероятности.

Контрольные вопросы:

· Какие задачи решает математическая статистика?

· Дайте определение генеральной и выборочной совокупностей, варианты, вариационного ряда, статистического распределения для выборки и эмпирической функции распределения;

· Что мы понимаем под репрезентативностью, эффективностью и состоятельностью выборки?

· Что значит несмещенность выборочной средней и смещенность выборочной дисперсии?

· В чем отличие интервальных оценок от точечных оценок параметров распределения по результатам выборки? Почему говорят, что интервал покрывает значение параметра с заданной надежностью, а концы интервала случайные величины? Что мы называем “надежностью”?

· В чем заключается метод моментов для точечной оценки параметров распределения?

· В чем состоит метод наибольшего правдоподобия?

· Могут ли коррелированные признаки элементов выборочной совокупности быть независимыми? Что значит равенство выборочного коэффициента корреляции ±1?

Вариант № 31

X– число членов семьи, занимающегося фермерским хозяйством (ед.)

Y – прибыль, получаемая фермерским хозяйством в среднем за сезон (тыс. долларов.)

Заданный признак: X и γ = 0.95

Таблицу частот см в вашем задании, файл «Вариант задания 4»