Институт управления и информационных технологий

ПУТЕЙ СООБЩЕНИЯ» (МИИТ)

ИНСТИТУТ УПРАВЛЕНИЯ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Кафедра Вычислительные системы и сети

Лекции по учебной дисциплине

«МОДЕЛИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ»

Направление: 09.03.01 «Информатика и вычислительная техника».

Профиль: «Вычислительные машины, комплексы, системы и сети».

Квалификация (степень) выпускника: магистр.

Форма обучения: очная.

Москва 2016 г.

Цели и задачи изучения дисциплины «Моделирование вычислительных систем» определяются характеристикой области и объектов профессиональной деятельности магистранта профиля «Компьютерные сети и технологии» направления подготовки «Информатика и вычислительная техника».

Цель изучения дисциплины состоит в освоении студентами методов и средств моделирования, необходимых для разработки, исследования и эксплуатации вычислительных систем и сетей.

В результате изучения дисциплины студенты должны владеть базовыми основами методологии моделирования вычислительных систем (ВС).

При изучении дисциплины излагаются типовые математические схемы моделирования вычислительных систем, вопросы формализации и алгоритмизации информационных процессов, современные подходы и методы моделирования сложных вычислительных систем и сетей.

Дисциплина «Моделирование вычислительных систем» относится к базовой части общенаучного учебного цикла М1.Б2. Профессиональный ФГОС ВПО.

Дисциплина имеет логическую и содержательно-методическую взаимосвязь с дисциплинами «Современные тенденции развития вычислительных систем и информационных технологий», «Математические методы GRID-технологий», «Проектирование вычислительных сетей».

При освоении дисциплины необходимы базовые знания по теории алгоритмов, организации вычислительных систем и сетей, сетям и телекоммуникациям, основам математического и системного анализа, дискретной математики, программированию.

Знания, умения и навыки, формируемые дисциплиной «Моделирование вычислительных систем», необходимы при изучении последующих дисциплин учебного плана: «Интегральные сети передачи данных», «Технологии глобальных сетей», «Проектирование вычислительных сетей», «Безопасность сетей».

ОСНОВНЫЕ ТЕМЫ ЛЕКЦИЙ

1. ВВЕДЕНИЕ В ДИСЦИПЛИНУ

2. ПОДХОДЫ К МОДЕЛИРОВАНИЮ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ

3. ВИДЫ МОДЕЛЕЙ ВС, ИХ ОСОБЕННОСТИ, ПРЕИМУЩЕСТВА И НЕДОСТАТКИ

4. ОБЩАЯ ТЕХНОЛОГИЯ МОДЕЛИРОВАНИЯ ВС

МАТЕМАТИЧЕСКИЕ МЕТОДЫ МОДЕЛИРОВАНИЯ ИНФОРМАЦИОННЫХ

ПРОЦЕССОВ В СЕТЯХ

6. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ВС

7. МНОГОУРОВНЕВЫЙ ПОДХОД К МОДЕЛИРОВАНИЮ ВЫЧИСЛИТЕЛЬНЫХ

СЕТЕЙ

8. МЕТОДЫ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ В ПРОЦЕССЕ

МНОГОВАРИАНТНОГО МОДЕЛИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ

АНАЛИЗ И ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ ВС

10. ЛИТЕРАТУРА

1. ВВЕДЕНИЕ В ДИСЦИПЛИНУ

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МОДЕЛИРОВАНИЯ

Модель - это система, исследование которой служит средством для получения информации о другой системе, это упрощённое представление реального устройства и/или протекающих в нём процессов, явлений.

Построение и исследование моделей, то есть моделирование, облегчает изучение имеющихся в реальном устройстве (процессе) свойств и закономерностей. Моделирование является обязательной частью исследований и разработок.

На рис.1 приведена классификация наиболее общих видов моделей вычислительных систем (ВС).

Рис.1 – Методы и средства моделирования ВС

Моделирование проходит три этапа:

1. Создание модели.

2. Изучение модели.

3. Применение результатов исследования на практике и/или формулирование теоретических выводов.

ПОДХОДЫ К МОДЕЛИРОВАНИЮ ВС

КЛАССИФИКАЦИЯ МОДЕЛЕЙ

По целям исследований

В зависимости от целей исследования выделяют следующие модели:

· функциональные. Предназначены для изучения особенностей работы (функционирования) системы, её назначения во взаимосвязи с внутренними и внешними элементами;

· функционально-физические. Предназначены для изучения физических (реальных) явлений, используемых для реализации заложенных в систему функций;

· модели процессов и явлений, такие как кинематические, прочностные, динамические и другие. Предназначены для исследования тех или иных свойств и характеристик системы, обеспечивающих её эффективное функционирование.

ТРЕБОВАНИЯ К МОДЕЛЯМ

Моделирование всегда предполагает принятие допущений той или иной степени важности. При этом должны удовлетворяться следующие требования к моделям:

· адекватность, то есть соответствие модели исходной реальной системе и учет, прежде всего, наиболее важных качеств, связей и характеристик. Оценить адекватность выбранной модели, особенно, например, на начальной стадии проектирования, когда вид создаваемой системы ещё неизвестен, очень сложно. В такой ситуации часто полагаются на опыт предшествующих разработок или применяют определённые методы;

· точность, то есть степень совпадения полученных в процессе моделирования результатов с заранее установленными, желаемыми. Здесь важной задачей является оценка потребной точности результатов и имеющейся точности исходных данных, согласование их как между собой, так и с точностью используемой модели;

· универсальность, то есть применимость модели к анализу ряда однотипных систем в одном или нескольких режимах функционирования. Это позволяет расширить область применимости модели для решения большего круга задач;

· целесообразная экономичность, то есть точность получаемых результатов и общность решения задачи должны увязываться с затратами на моделирование. И удачный выбор модели, как показывает практика, — результат компромисса между отпущенными ресурсами и особенностями используемой модели;

· и др.

Выбор модели и обеспечение точности моделирования считается одной из самых важных задач моделирования.

Точность моделей

Погрешности моделирования вызываются как объективными причинами, связанными с упрощением реальных систем, так и субъективными, обусловленными недостатком знаний и навыков, особенностями характера того или иного человека. Погрешности можно предотвратить, компенсировать или учесть. И всегда обязательна оценка правильности получаемых результатов. В технике быструю оценку точности модели часто проводят следующими способами:

· проверяют соответствие результатов физическому (здравому) смыслу. Удобно это делать для частного случая модели, когда решение очевидно. Иногда даже говорят, что ещё перед решением задачи инженер уже должен представлять характер и порядок ожидаемого результата. Но точность такого представления зависит от развитости физического воображения и опыта работы с подобными системами;

· проверяют выполнение частных очевидных условий задачи, что также позволяет отсечь неприемлемые решения;

· проверяют соблюдение тенденции изменения величин и знаков результатов (монотонность, цикличность, плавность и т. п.);

· проверяют правильность размерности полученного результата (если работа ведется с аналитическими зависимостями).

Известно, что посредством грубых измерений невозможно получить точные результаты. С другой стороны, бессмысленно вести, например, расчет с точностью до грамма, если результат потом нужно округлять с точностью до ста грамм, или же определять среднюю величину точнее составляющих её значений, и т. д. Поэтому важно помнить о следующем:

· точность результатов расчетов и экспериментальных исследований модели не может превысить точности исходных данных, используемых приборов и т. п.;

· вид выбираемой модели должен согласовываться с точностью исходных данных и потребной точностью результатов;

· желаемая точность результатов должна соответствовать нуждам и реалиям практики.

Основные виды моделей

По способу отображения действительности различают три основных вида моделей — эвристические, натурные и математические.

ВИДЫ МОДЕЛЕЙ

Эвристические модели

Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека. Их описание ведется словами естественного языка (например, вербальная информационная модель) и, обычно, неоднозначно и субъективно. Эти модели неформализуемы, то есть не описываются формально-логическими и математическими выражениями, хотя и рождаются на основе представления реальных процессов и явлений.

Эвристическое моделирование — основное средство вырваться за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии человека, его опыта и эрудиции. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе ещё скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.

Натурные модели

Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие:

· Физические модели. Ими являются реальные изделия, образцы, экспериментальные и натурные модели, когда между параметрами системы и модели одинаковой физической природы существует однозначное соответствие. Выбор размеров таких моделей ведётся с соблюдением теории подобия. Физические модели подразделяются на объёмные (модели и макеты) и плоские (тремплеты):

o в данном случае под (физической) моделью понимают изделие или устройство, являющееся упрощённым подобием исследуемого объекта или позволяющее воссоздать исследуемый процесс или явление. Например, предметные модели, как уменьшенные копии оригинала (глобус как модель Земли, игрушечный самолёт с учётом его аэродинамики);

o под тремплетом понимают изделие, являющееся плоским масштабным отображением объекта в виде упрощённой ортогональной проекции или его контурным очертанием. Тремплетеотанарные вырезают из плёнки, картона и т. п., и применяют при исследовании и проектировании зданий, установок, сооружений;

o под макетом понимают изделие, собранное из моделей и/или тремплетов.

Физическое моделирование — основа наших знаний и средство проверки наших гипотез и результатов расчётов. Физическая модель позволяет охватить явление или процесс во всём их многообразии, наиболее адекватна и точна, но достаточно дорога, трудоёмка и менее универсальна. В том или ином виде с физическими моделями работают на всех этапах проектирования.

Математические модели

Математические модели — формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:

· аналитические модели. Их решения ищутся в замкнутом виде, в виде функциональных зависимостей. Удобны при анализе сущности описываемого явления или процесса и использовании в других математических моделях, но отыскание их решений бывает весьма затруднено;

· численные модели. Их решения — дискретный ряд чисел (таблицы). Модели универсальны, удобны для решения сложных задач, но не наглядны и трудоемки при анализе и установлении взаимосвязей между параметрами. В настоящее время такие модели реализуют в виде программных комплексов — пакетов программ для расчета на компьютере. Программные комплексы бывают прикладные, привязанные к предметной области и конкретному объекту, явлению, процессу, и общие, реализующие универсальные математические соотношения (например, расчет системы алгебраических уравнений);

· формально-логические информационные модели — это модели, созданные на формальном языке.

Построение математических моделей возможно следующими способами:

· аналитическим путём, то есть выводом из физических законов, математических аксиом или теорем;

· экспериментальным путём, то есть посредством обработки результатов эксперимента и подбора аппроксимирующих (приближённо совпадающих) зависимостей.

Математические модели более универсальны и дешевы, позволяют поставить «чистый» эксперимент (то есть в пределах точности модели исследовать влияние какого-то отдельного параметра при постоянстве других), прогнозировать развитие явления или процесса, отыскать способы управления ими. Математические модели — основа построения компьютерных моделей и применения вычислительной техники.

Результаты математического моделирования нуждаются в обязательном сопоставлении с данными физического моделирования — с целью проверки получаемых данных и для уточнения самой модели. С другой стороны, любая формула — это разновидность модели.

Промежуточные виды моделей

К промежуточным видам моделей можно отнести:

Трёхмерная компьютерная модель

· графические модели. Занимают промежуточное место между эвристическими и математическими моделями. Представляют собой различные изображения:

o графы;

o схемы;

o эскизы. Этому упрощенному изображению некоторого устройства в значительной степени присущи эвристические черты;

o чертежи. Здесь уже конкретизированы внутренние и внешние связи моделируемого (проектируемого) устройства, его размеры;

o графики;

o полигонная модель в компьютерной графике как образ объекта, «сшитый» из множества многоугольников.

· аналоговые модели. Позволяют исследовать одни физические явления или математические выражения посредством изучения других физических явлений, имеющих аналогичные математические модели. В качестве примера можно привести метод динамических аналогий, широко применяемый в акустике, а также в механике;

· и др.

Существует и другие виды «пограничных» моделей, например, экономико-математическая и т. д.

Выбор типа модели зависит от объема и характера исходной информации о рассматриваемом устройстве и возможностей инженера, исследователя. По возрастанию степени соответствия реальности модели можно расположить в следующий ряд: эвристические (образные) — математические — натурные (экспериментальные).

Уровни моделей

Количество параметров, характеризующих поведение не только реальной системы, но и её модели, очень велико. Для упрощения процесса изучения реальных систем выделяют четыре уровня их моделей, различающиеся количеством и степенью важности учитываемых свойств и параметров. Это — функциональная, принципиальная, структурная и параметрическая модели.

Функциональная модель

Функциональная модель предназначена для изучения особенностей работы (функционирования) системы и её назначения во взаимосвязи с внутренними и внешними элементами.

Функция — самая существенная характеристика любой системы, отражает её предназначение, то, ради чего она была создана. Подобные модели оперируют, прежде всего, с функциональными параметрами. Графическим представлением этих моделей служат блок-схемы. Они отображают порядок действий, направленных на достижение заданных целей (т. н. 'функциональная схема'). Функциональной моделью является абстрактная модель.

Модель принципа действия

Модель принципа действия (принципиальная модель, концептуальная модель) характеризует самые существенные (принципиальные) связи и свойства реальной системы. Это — основополагающие физические, биологические, химические, социальные и т. п. явления, обеспечивающие функционирование системы, или любые другие принципиальные положения, на которых базируется планируемая деятельность или исследуемый процесс. Стремятся к тому, чтобы количество учитываемых свойств и характеризующих их параметров было небольшим (оставляют наиболее важные), а обозримость модели — максимальной, так чтобы трудоемкость работы с моделью не отвлекала внимание от сущности исследуемых явлений. Как правило, описывающие подобные модели параметры — функциональные, а также физические характеристики процессов и явлений. Принципиальные исходные положения (методы, способы, направления и т. д.) лежат в основе любой деятельности или работы.

Так, принцип действия технической системы — это последовательность выполнения определённых действий, базирующихся на определённых физических явлениях (эффектах), которые обеспечивают требуемое функционирование этой системы.

Примеры моделей принципа действия: фундаментальные и прикладные науки (например, принцип построения модели, исходные принципы решения задачи), общественная жизнь (например, принципы отбора кандидатов, оказания помощи), экономика (например, принципы налогообложения, исчисления прибыли), культура (например, художественные принципы).

Работа с моделями принципа действия позволяет определить перспективные направления разработки (например, механика или электротехника) и требования к возможным материалам (твердые или жидкие, металлические или неметаллические, магнитные или немагнитные и т. д.).

Графическим представлением моделей принципа действия служат блок-схема, функциональная схема, принципиальная схема.

Например, для технических моделей эти схемы отражают процесс преобразования вещества, как материальной основы устройства, посредством определённых энергетических воздействий с целью реализации потребных функций (функционально-физическая схема). На схеме виды и направления воздействия, например, изображаются стрелками, а объекты воздействия — прямоугольниками.

Структурная модель

Четкого определения структурной модели не существует. Так, под структурной моделью устройства могут подразумевать:

· структурную схему, которая представляет собой упрощенное графическое изображение устройства, дающее общее представление о форме, расположении и числе наиболее важных его частей и их взаимных связях;

· топологическую модель, которая отражает взаимные связи между объектами, не зависящие от их геометрических свойств.

Под структурной моделью процесса обычно подразумевают характеризующую его последовательность и состав стадий и этапов работы, совокупность процедур и привлекаемых технических средств, взаимодействие участников процесса.

Например, — это могут быть упрощенное изображение звеньев механизма в виде стержней, плоских фигур (механика), прямоугольники с линиями со стрелками (теория автоматического управления, блок-схемы алгоритмов), план литературного произведения или законопроекта и т. д. Степень упрощения зависит от полноты исходных данных об исследуемом устройстве и потребной точности результатов. На практике виды структурных схем могут варьироваться от несложных небольших схем (минимальное число частей, простота форм их поверхностей) до близких к чертежу изображений (высокая степень подробности описания, сложность используемых форм поверхностей).

Возможно изображение структурной схемы в масштабе. Такую модель относят к структурно-параметрической. Её примером служит кинематическая схема механизма, на которой размеры упрощенно изображенных звеньев (длины линий-стержней, радиусы колес-окружностей и т. д.) нанесены в масштабе, что позволяет дать численную оценку некоторым исследуемым характеристикам.

Для повышения полноты восприятия на структурных схемах в символьном (буквенном, условными знаками) виде могут указывать параметры, характеризующие свойства отображаемых систем. Исследование таких схем позволяет установить соотношения (функциональные, геометрические и т. п.) между этими параметрами, то есть представить их взаимосвязь в виде равенств f (x₁, х₂, …) = 0, неравенств f (x₁, х₂, …) > 0 и в иных выражениях.

Параметрическая модель

Под параметрической моделью понимается математическая модель, позволяющая установить количественную связь между функциональными и вспомогательными параметрами системы. Графической интерпретацией такой модели в технике служит чертеж устройства или его частей с указанием численных значений параметров.

4. ОБЩАЯ ТЕХНОЛОГИЯ МОДЕЛИРОВАНИЯ ВС

ПРОБЛЕМЫ МОДЕЛИРОВАНИЯ ВС

Стохастические модели

У существующих аналитических стохастических методов обнаруживаются ограниченные возможности по применению, связанные с допущениями о входящих пуассоновских или эрлановских потоках, не позволяющих описывать сложные процессы, происходящие в узлах сетей и в каналах связи.

Тензоры

Применение тензорной методологии для анализа и создания современных сетей, предоставляющей собой математический аппарат, позволяющий описывать сложные системы. Тензорный подход – это достаточно формализованная теория, где методы расчёта, представленные в матричной форме, можно эффективно реализовать на ЭВМ. Несомненно, что тензорные модели подходят для расчета и оптимизации некоторых характеристик сетей, но строить весь процесс создания на тензорной теории, учитывая особенности таких сетей вряд ли целесообразно.

Синергетические модели

Для создания моделей глобальных, территориальных и региональных сетей в последнее время стали использоваться идеи синергетики – группы методов построения аналитических моделей сложных самоорганизующихся систем, предназначенных преимущественно для качественного описания их функционирования, но с широкими возможностями индикации проявлений неожиданных событий в процессе развития и функционирования сети. Синергетические модели имеют перспективы применительно к конкретному анализу и стратегическому планированию сетей, однако сейчас они являются еще не достаточно «апробированными».

Имитационные модели

Особым классом математических моделей являются имитационные модели. Имитационные модели сетей воспроизводят процессы генерации сообщений приложениями, разбиение сообщений на пакеты и кадры определенных протоколов, задержки, связанные с обработкой сообщений, пакетов и кадров внутри ОС, процесс получения доступа компьютером к разделяемой сетевой среде, процесс обработки поступающих пакетов маршрутизатором и т.д. При имитационном моделировании сети не требуется приобретать дорогостоящее оборудование - его работы имитируется программами, достаточно точно воспроизводящими все основные особенности и параметры такого оборудования. Преимуществом имитационных моделей является возможность подмены процесса смены событий в исследуемой системе в реальном масштабе времени на ускоренный процесс смены событий в темпе работы программы. В результате за несколько минут можно воспроизвести функционирование сети в течение нескольких дней, что дает возможность оценить ее работу в широком диапазоне варьируемых параметров. Также основным достоинством имитационных моделей является отсутствие ряда допущений, свойственных аналитическим моделям. Необходимо отметить такое преимущество имитационных моделей, как возможность построения гистограмм распределения случайных величин. Современные системы имитационного моделирования обычно позволяют задавать модели либо путем непосредственного написания ее кода на специальных языках, таких, как GPSS и SIMSCRIPT, либо использовать визуальные конструкторы, которые позволяют значительно сократить время создания модели. Для наиболее развитых систем характерно применение параметризованных моделей, реализуемых с помощью специальных мастеров «визардов». Результатом работы имитационной модели являются собранные в ходе наблюдения за протекающими событиями статистические данные о наиболее важных характеристиках сети: времени реакции, коэффициентах использования каналов и узлов, вероятности потерь пакетов и т.п. Частным случаем имитационных моделей являются эмуляционные или полунатурные модели (так называемая имитация в реальном времени). Однако при имитационном моделировании имеется и ряд трудностей, прежде всего это использование интерфейсов прикладного программирования или объектных моделей документов, уникальных для каждой системы имитационного моделирования. Также для имитационного моделирования существенным является дисбаланс временных масштабов – например, например, интервалы между поступлениями запросов клиентов исчисляются секундами и десятками секунд, а временной масштаб событий, определяемых протоколом радиосоты, измеряется в микросекундах.

Физическая модель

При физическом моделировании исследуемая система заменяется соответствующей ей другой материальной системой. Примером этого вида моделирования может служить «пилотная» сеть, с помощью которой изучается принципиальная возможность построения сети на основе тех или иных компьютеров, коммуникационных устройств, ОС и приложений. Возможности физического моделирования ограничены. Оно позволяет решать отдельные задачи при задании небольшого количества сочетаний исследуемых параметров сети. При физическом моделировании сети практически невозможно проверить ее работу для вариантов с использованием различных типов коммуникационных устройств - маршрутизаторов, коммутаторов и т.п. Проверка на практике около десятка разных типов маршрутизаторов связана не только с большими усилиями и временными затратами, но и с немалыми материальными затратами. Даже и в тех случаях, когда при оптимизации сети изменяются не типы устройств и ОС, а только их параметры, проведение экспериментов в реальном масштабе времени для огромного количества всевозможных сочетаний этих параметров практически невозможно за обозримое время. Простое изменение максимального размера пакета в каком-либо протоколе требует переконфигурирования ОС в сотнях компьютеров сети, что требует от администратора проведения очень большой работы. Поэтому, при создании и адаптации корпоративных функционально-ориентированных сетей во многих случаях предпочтительным оказывается использование математического моделирования.

ВЫБОР УРОВНЯ ДЕТАЛИЗАЦИИ ВС

ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ

Пропускная способность узла

Пусть 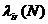- интенсивность потока (i,r)-заданий, поступающих в узел i сети Q(M,N) в стационарном режиме. Очевидно, что 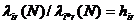- относительная частота посещения r-заявкой узла 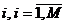, приходящаяся на одно посещение некоторого выделенного УК i*. Интенсивность 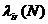поступающего в узел i потока r-заявок равна интенсивности обслуженного этим узлом потока r-заявок.

Следовательно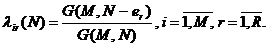

При этом, маргинальное распределение общего числа заявок в узле удовлетворяет рекуррентному соотношению:

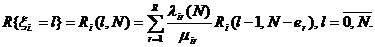
ЯЗЫК МОДЕЛИРОВАНИЯ GPSS

Блок-схемы

Использование блок-схем является удобной базой для языка модели-рования GPSS. Для этого моделируемая система должна быть представлена в виде последовательности стандартных блоков.

Тогда в процессе моделирования программа будет создавать транзакты, продвигать их через определенные блоки и выполнять действия, соответст-вующие каждому из этих блоков, т.е. блок-схема показывает путь продвиже-ния транзактов и последовательность их обработки различными блоками,

При построении блок-схемы в первую очередь выделяются логические сегменты системы и блоки, представляющие основные функции, выполняе-мые системой. После этого производится детализация логики системы добав-лением блоков, выполняющих менее важные операции.

Внесение транзактов в модель производится с помощью блока GENERATE (ГЕНЕРИРОВАТЬ). Информация, необходимая для определения случайного интервала между моментами поступления транзактов, задается операндами Аи В. В поле Азадается среднее значение времени, а в поле В- модификатор. При этом аргумент поля Вможет быть задан одним из двух способов:

1. Посредством модификатора интервала. Эта константа определяет ин-тервал, в котором времена распределены равномерно. Любое из (2В+1) целых чисел, заключенных в интервале (А-В, А+В), будут выбираться с вероятностью 1/(2В+1).

2. Посредством модификатора-функции. При этом в поле В должен быть записан модификатор-функция, а вычисленное значение атрибута, за-данного в поле А, умножается на значение функции, заданной в поле В.

Поле Сопределяет интервал смещения, предшествующий возникнове-нию в блоке первого транзакта.

Поле Dограничивает число транзактов, которые должны быть созданы блоком GENERATE. Если поле является пустым, то блок будет генерировать транзакты без ограничения. Уровень приоритета задается в поле Е.

Каждый транзакт может иметь определенное число параметров, в кото-рые записываются его характеристики. Групповым именем параметра являет-ся буква Р, Например, Р12, P$SLED означают значения двенадцатого пара-метра транзакта и параметра с именем SLED.

В процессе моделирования параметры транзакта могут изменяться и назначаться при входе в блок ASSIGN. В момент создания транзакта все его параметры равны 0. В поле Азадается номер или имя параметра. Непосред-ственно за аргументом поля Аможет не стоять никакого знака или же стоять знак "+" или "-". Эти знаки показывают, как будет использовано значение по-ля В: будет ли оно заменять текущее значение параметра или же будет сум-мироваться (вычитаться) с текущим значением.

Транзакты удаляются из модели, попадая в блок TERMINATE. В моде-ли может быть любое число блоков TERMINATE. Операнд Аявляется ука-зателем уменьшения счетчика завершения. При входе транзакта в блок TERMINATE значение счетчика завершения уменьшается на число, указан-ное в операнде А.

Начальное значение счетчика завершения задается в поле Акарты START. Как только в процессе моделирования значение счетчика становится равным нулю, моделирование завершается.

Косвенная адресация

Иногда при моделировании возникают ситуации, при которых в качестве исходного данного должен использоваться СЧА, номер которого зависит от свойств транзакта, производящего ссылку на этот СЧА.

В GPSS/PC косвенная адресация осуществляется через значения параметров транзактов. При записи между соответствующим СЧА и номером параметра ставится знак *. Например, Q*6 - величина текущего содержимого очереди, номер которой записан в шестом параметре транзакта; FN*3 - значение функции, номер которой записан в третьем параметре транзакта.

Выбор масштаба времени

В GPSS используются целочисленные значения моментов времени. Поэтому неправильный выбор масштаба времени может привести к значи-тельной погрешности. Масштаб времени определяется разработчиком модели и зависит от значения тех временных интервалов, которые задаются в соот-ветствующих блоках модели.

В системе моделирования GPSS World используется вещественные значения модельного времени, поэтому при ее использовании можно обойтись без масштабирования.

МОДЕЛИ СЕТЕЙ И ИХ ЭЛЕМЕНТОВ

На основе проведенного выше анализа моделей сетей и методов моделирования, а также с учетом того, что корпоративная функционально-ориентированная сеть представляет собой динамическую систему, можно сделать вывод о том, что в комплекс могут входить следующие виды математических моделей:

· По способу представления свойств сети - аналитические, алгоритмические и имитационные модели. Аналитические математические модели - здесь важным моментом является их размерность. Часто для реальных сетей размерность их аналитических моделей столь велика, что получение оптимального решения оказывается весьма сложным с вычислительной точки зрения. Для повышения вычислительной эффективности в этом случае используют различные приемы. Один из них связан с разбиением задачи большой размерности на подзадачи меньшей размерности так, чтобы автономные решения подзадач в определенной последовательности давали решение основной задачи. При этом возникают проблемы организации взаимодействия подзадач, которые не всегда оказываются простыми. Другой прием предполагает уменьшение точности вычислений, за счет чего удается сократить время решения задачи.

· По характеру отображаемых свойств сетей - структурные (предназначенные для отображения структурных свойств сети и сетевых элементов) и функциональные математические модели (предназначенные для отображения информационных, физических и временных процессов, протекающих в работающей сети).

· По способу получения модели – теоретические (созданные в результате исследования сетей теоретическом уровне) и эмпирические (полученные в результате проведения экспериментов и обработки результатов методами математической статистики).

· По особенности поведения сети или сетевого элемента – детерминированные и вероятностные.

Форма представления моделей

Модели аналитические и имитационные при многоуровневом представлении сетей целесообразно представить в виде следующей зависимости:

модель_{номер модели} : {список входных параметров}Þ

Þ выходные параметры (или параметр)

Каждая модель имеет свой вектор признаков:

M = или m = ,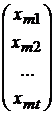

где компоненты x_Mi и x_mj, векторов Mи mхарактеризуют наличие i-го

(j-го)признака.

В вектор признаков входят: номер уровня модели OSI и номер самой модели, принадлежность соответствующим уровням, принадлежность определенному классу (подклассу) задач; время расчета данной характеристики, входные и выходные параметры.

МЕТОДЫ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ В ПРОЦЕССЕ МНОГОВАРИАНТНОГО МОДЕЛИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ СЕТЕЙ

МЕТОДЫ ФОРМИРОВАНИЕ МНОЖЕСТВА РАЦИОНАЛЬНЫХ ВАРИАНТОВ

Рис. Формирование множества альтернативных вариантов сети и выбор базового решения

КАЛИБРОВКА МОДЕЛЕЙ

Если в результате проведенной оценки качества модели оказалось, что ее целевые свойства не удовлетворяют разработчика, необходимо выполнить ее калибровку, то есть коррекцию с целью приведения в соответствие предъявляемым требованиям. Как правило, процесс калибровки носит итеративный характер и состоит из трех основных этапов:

· глобальные изменения модели (например, введение новых процессов, изменение типов событий и т. д.);

· локальные изменения (в частности, изменение некоторых законов распределения моделируемых случайных величин);

· изменение специальных параметров, называемых калибровочными.

На первый взгляд, структурные изм