Типовые алгоритмы моделирования потоков

Общий подход для моделирования стационарных потоков с ограниченным последействием и заданным 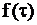заключается в следующем.

1. Формируется момент времени наступления первого события в соответствии с соотношениями

, , ,

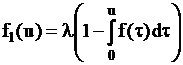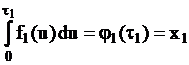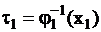где 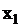равномерно распределенная на интервале 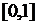случайная величина. Отсюда .

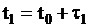2. Последующие вызывающие моменты определяются следующим образом:

, , ,

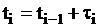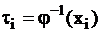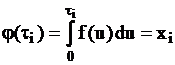где 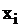, 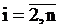последовательность равномерно распределенных случайных величин на интервале .

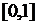Поток Пуассона. 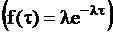. Плотность 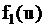имеет вид

.

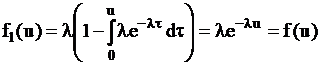Первый интервал распределен так же, как и остальные. Отсюда для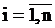

, , .

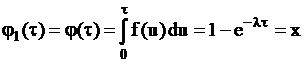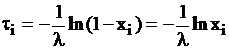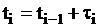Поток Эрланга. 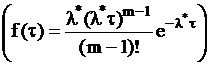. Пусть 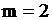, тогда

, .

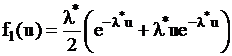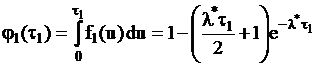Для нахождения 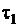требуется решать трансцендентное уравнение

, .

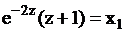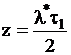Для 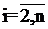интервалы времени между событиями формируются с учетом того, что

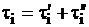
есть сумма двух одинаково распределенных по показательному закону случайных величин с параметром 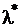. Тогда

, , ,

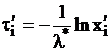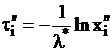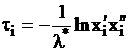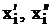– независимые значения равновероятной случайной величины.

Если реализация достаточно длинная, то можно положить 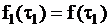и существенно упростить процедуру моделирования (исключить решение трансцендентного уравнения), что особенно важно при генерации потоков высших порядков по аналогичной методике.

Нестационарный поток Пуассона. Данный поток характеризуется зависящей от времени интенсивностью 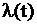и законом распределения числа событий 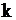на интервале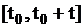

, .

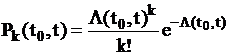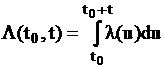Во многих случаях изменения интенсивности происходят медленнее, чем интервалы между событиями. Тогда приближенно

, .

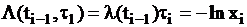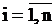Для моделирования неординарных потоков событий(при произвольном 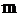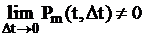), кроме задания законов распределения вызывающих моментов времени 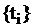, необходимо дополнительно задавать распределение количеством событий, поступающих в рассматриваемые моменты времени.

15.Сущность метода имитационного моделирования применительно к исследованию СМО. Алгоритмы генерации потоков событий (1,2,3).

Реализация технологий имитационного моделирования применительно к задачам исследования СМО предполагает:

1) построение алгоритмов и программных модулей, вырабатывающих реализации случайных потоков однородных и неоднородных событий – «генераторов» источников;

2) построение моделирующих алгоритмов и программных модулей, описывающих функционирование отдельных элементов, а также СМО в целом в соответствии с ее структурой и внутренними параметрами;

3) многократное воспроизведение входных потоков и общего процесса обслуживания, а также обработку получаемых данных в интересах оценки показателей эффективности данного типа СМО.

Элементы СМО разделяют на активные, пассивные и активно-пассивные.

Активными элементами называются такие, смена состояний которых обусловлена только их внутренними свойствами.

Пассивныминазываются такие элементы, которые изменяют свои свойства только под воздействием активных элементов, а, в общем случае, любых внешних факторов.

Активно-пассивными элементами называются такие, которые в одном из своих возможных состояний являются активными, а в других – пассивными.

Активные элементы – источники заявок.

Пассивные элементы – накопители заявок.

Активно-пассивные элементы – каналы обслуживания заявок.

I.Генерация входных потоков

Случайным потоком называется последовательность событий, следующих одно за другим в некоторые, вообще говоря, случайные моменты времени 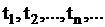При построении генераторов случайных потоков следует, прежде всего, определить тип потока событий, который требуется воспроизвести.

1.Однородность–неоднородность

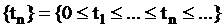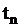Однородный поток – характеризуется только моментами наступления событий (вызывающими моментами) и задается случайной последовательностью , где – момент наступления 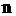-го события (неотрицательное вещественное число).

Однородный поток также может быть задан в виде случайной последовательности интервалов времени между событиями , ( , ).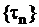

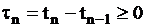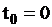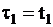Неоднородный поток – характеризуется случайной последовательностью 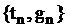, где 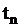– вызывающие моменты, а 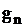– набор признаков события, изменяющихся по детерминированному или случайному закону в зависимости от .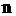