Алгоритм обслуживания заявок

В процессе разработки программы следует придерживаться следующего алгоритма.

Генератор заявок генерирует некоторый случайным образом распределенный во времени поток событий. Система обслуживания с 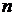каналами работает следующим образом: 1-ая заявка поступает на 1-ый канал, следующая заявка в случае, если занят 1-ый канал – поступает на 2-ой, следующая заявка поступает на 3-ий, если первые два канала заняты и т.д. Если все 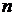каналов заняты, то поступившая заявка получает отказ и формируется файл в виде случайного потока отказов. Если освобождается несколько каналов, то текущая заявка поступает в канал, имеющий меньший номер. Система обслуживания обрабатывает заявки, исходя из собственного времени обслуживания каждого канала и выдает потоки обслуженных заявок. На выходе системы должны быть сформированы 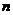файлов в виде случайных потоков обслуженных заявок.

Порядок выполнения работы

1. Генератр заявок представляется в виде подпрограммы, генерирующей поток событий, сформированный каждым студентом в 4-ой лабораторной работе.

2. Время обслуживания текущей заявки 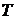для каждого канала является случайной величиной и определяется согласно данных варианта и уравнения (5.3). Соответствующая подпрограмма, имитирующая время обслуживания, создается на основе использования простейшего генератора случайного события, имеющего Пуассоновское распределение. Соответствующий алгоритм приведен в указаниях к выполнению 4-ой лабораторной работе на рисунке 4.1.

3. Вся система должна функционировать в соответствии с алгоритмом, приведенным в пункте 5.3.

4. В результате иммитационного моделирования необходимо сформировать 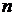файлов для потока обслуживаемых заявок и 1 файл для потока отказов.

5. Найти количество обслуженных заявок по каждому каналу и количество отказов. Определить среднюю интенсивность обслуженных заявок в единицу времени и интенсивность отказов.

6. Определить вероятность отказов и вероятность обслуживания для каждого канала по числу отказов и обслуживаний и числу всех событий.

Варианты заданий

№	Число каналов		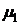		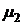		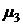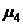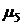Приме-чание
		0,03	0,05	0,01	–	–
		0,06	0,08	0,04	0,09	–
		0,08	0,07	0,06	0,05	0,03
		0,04	0,03	0,01	–	–
		0,3	0,05	0,07	0,02	–
		0,07	0,04	0,03	0,09	0,075
		0,04	0,01	0,02	–	–
		0,05	0,02	0,05	0,06	–
		0,09	0,005	0,01	0,05	0,07
		0,01	0,02	0,04	–	–
		0,02	0,05	0,01	0,04	–
		0,07	0,06	0,09	0,02	0,08
		0,03	0,04	0,05	–	–
		0,05	0,03	0,08	0,07	–
		0,07	0,05	0,09	0,04	0,08
		0,04	0,07	0,06	–	–
		0,03	0,02	0,01	0,01	–
		0,09	0,07	0,05	0,08	0,04
		0,05	0,09	0,07	–	–
		0,02	0,07	0,01	0,04	–
		0,07	0,01	0,06	0,02	0,01
		0,04	0,06	0,02	–	–
		0,06	0,04	0,03	0,07	–

5.6 Контрольные вопросы

1. Основные свойства простейшего потока?

2. Что характеризует параметр 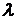в экспоненциальном законе распределения?

3. Что характеризует параметр 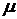в экспоненциальном законе распределения?

4. Что описывает закон распределения Пуассона?

5. Что представляет собой последействие в случайном потоке?

6. Каковы особенности потока Пальма?

7. Какая величина изменяется случайным образом в случайном потоке: а) на входе сервера (системы обслуживания); б) на выходе сервера ?

8. Что такое пропускная способность СМО?

9. Что представляет собой производительность источника?

5.6 Рекомендуемая литература

1. Е.С. Вентцель Теория вероятностей: учебник для втузов / Е.С. Вентцель. 8-е изд., перераб. и доп. – М. : Физматлит, 1999. – 576 с.

2. Моделирование информационных систем: уч. пос. /ред. О.И. Шелухина. – М.: Радиотехника, 2005. – 368 с.

Приложение А. – Основные сведения по генераторам случайных чисел

В основе метода Монте-Карло лежит генерация случайных чисел, которые должны быть равномерно распределены в интервале (0; 1).

Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи, решаемой статистическим методом, может оказаться неверным. Поэтому проблема использования хорошего генератора действительно случайных и действительно равномерно распределенных чисел стоит очень остро.

Математическое ожидание m_r и дисперсия D_r такой последовательности, состоящей из n случайных чисел r_i, должны быть следующими (если это действительно равномерно распределенные случайные числа в интервале от 0 до 1):

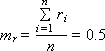
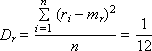
Если пользователю потребуется, чтобы случайное число x находилось в интервале (a; b), отличном от (0; 1), нужно воспользоваться формулой x = a + (b – a) · r, где r —

случайное число из интервала (0; 1). Законность данного преобразования демонстрируется нарисунке А.1.

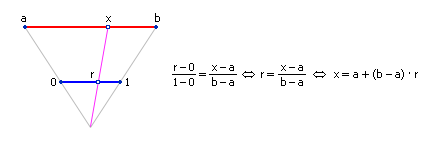Рис. А.1. Схема перевода числа из интервала (0; 1) в интервал (a; b)

Теперь x – случайное число, равномерно распределенное в диапазоне от a до b.

За эталон генератора случайных чисел (ГСЧ) принят такой генератор, который порождает последовательность случайных чисел с равномерным законом распределения в интервале (0; 1). За одно обращение данный генератор возвращает одно случайное число. Если наблюдать такой ГСЧ достаточно длительное время, то окажется, что, например, в каждый из десяти интервалов (0; 0.1), (0.1; 0.2), (0.2; 0.3), …, (0.9; 1) попадет практически одинаковое количество случайных чисел – то есть они будут распределены равномерно по всему интервалу (0; 1). Если изобразить на графике k = 10 интервалов и частоты N_i попаданий в них, то получится экспериментальная кривая плотности распределения случайных чисел (см. рис. А.2).

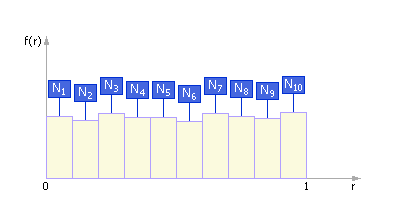Рис. А.2. Частотная диаграмма выпадения случайных чисел,
порождаемых реальным генератором

Заметим, что в идеале кривая плотности распределения случайных чисел выглядела бы так, как показано нарисунке А.3. То есть в идеальном случае в каждый интервал попадает одинаковое число точек: N_i = N/k, где N – общее число точек, k – количество интервалов, i = 1, …, k.

Функциональные преобразования для имитации случайных процессов

Случайные процессы имитируются в основном с использованием равномернораспределенного генератора случайных чисел.

Нормальное распределение моделируется следующими способами: