Моделирование случайных потоков
Систем массового обслуживания с отказами
Современное общество не может обойтись без разветвленной сети систем массового обслуживания. К таким системам относятся телефонные станции, магазины, поликлиники, предприятия общественного питания, билетные кассы, автозаправочные станции, парикмахерские и т.п. Несмотря на разнообразие, все эти системы имеют общие закономерности.
В ХХ веке возникло и стало развиваться новое направление в теории вероятностей, названное по предложению видного советского математика А.Я.Хинчина “Теорией массового обслуживания”. Начальный период в развитии теории связан с работами известного датского ученого А. Эрланга, которые относятся к 1908 – 1922 годам ХХ столетия.
Цель работы:изучение моделей случайных потоков; имитационное моделирование системы массового обслуживания с отказами; анализ статистических характеристик случайных потоков;.
Общие положения
Основные понятия. Любая система массового обслуживания предназначена для выполнения некоторого потока заявок. В роли заявки может выступать появление пассажира в билетной кассе, возникновение неисправности в устройстве, приход судна в порт, появление частицы в счетчике Гейгера Мюллера и т.д. Система может иметь одну или несколько обслуживающих единиц, которые принято называть каналами обслуживания. В парикмахерской количество работающих мастеров равно числу каналов обслуживания. В других ситуациях – это число кассиров в билетной кассе, число телефонов на переговорном пункте, число причалов в морском порту, число колонок на автозаправочной станции и т.д. Приходя в поликлинику к определенному врачу, мы имеем дело также с одноканальной системой массового обслуживания.
Рассматривая работу той или иной системы массового обслуживания, надо учитывать прежде всего число каналов обслуживания, число заявок, поступающих на вход системы в единицу времени, длительность обслуживания одной заявки. Существенно, что число поступающих в систему заявок, моменты их поступления, длительность обслуживания заявки и т.д. относятся, как правило, к категории случайных факторов. Поэтому теория массового обслуживания тесно связана с теорией случайных процессов.
В теории массового обслуживания чаще всего рассматриваются различные сучайные процессы. Чаще всего имеются в виду случайные процессы с дискретными состояниями. Переходы системы из одних состояний в другие происходят под действием потока заявок, поступающих на вход системы, и потока обслуживаний. Под последним понимается поток заявок, обслуживаемых одним непрерывно занятым каналом системы.
Виды систем массового обслуживания. Системы массового обслуживания бывают двух видов: системы с отказами и системы с очередью. Если заявка поступает в систему с отказами в момент времени, когда все каналы заняты, то она получает «отказ» и выходит из игры. Например, при звонке по телефону, если абонент занят, заявка получает отказ, и абонент может повесить трубку. Повторно набирая телефонный номер, абонент тем самым посылает новую заявку.
Наиболее часто на практике встречаются системы с очередью, или, иначе, системы с ожиданием. Недаром теорию массового обслуживания называют также теорией очередей. В таких системах заявка, появившаяся в момент, когда все каналы обслуживания заняты, встает в очередь и ожидает, пока не освободится один из каналов. Существуют системы с неограниченной очередью (стоящая в очереди заявка рано или поздно будет обслужена, при этом число мест в очереди не ограничено) и системы с ограниченной очередью. Ограничения могут быть разными – по числу заявок, одновременно стоящих в очереди (в очереди должно быть не больше некоторого числа заявок, всякая дополнительная заявка получает отказ); по времени пребывания заявки в очереди (после некоторого срока пребывания в очереди заявка, если она не начала обслуживаться, покидает очередь); по времени работы системы (прием заявок к обслуживанию происходит в течение определенного времени) и т.д.
При моделировании может также учитываться дисциплина обслуживания. Обычно заявки обслуживаются в порядке их поступления в систему. Но возможно также обслуживание с приоритетом, когда некоторые заявки обслуживаются вне очереди. При этом заявка с более высоким приоритетом, поступив в систему, может оборвать уже начавшееся обслуживание заявки с меньшим приоритетом, а может дождаться окончания предыдущего обслуживания. В первом случае говорят об абсолютном приоритете, а во втором – об относительном. Системы массового обслуживания всегда являются многокритериальными, они характеризуются набором показателей эффективности. В качестве таковых могут выступать среднее число заявок, которое обслуживает система в единицу времени; среднее число занятых каналов обслуживания; среднее число заявок, находящихся в очереди; среднее время ожидания обслуживания; средний процент заявок, получающих отказ; вероятность того, что поступившая в систему заявка, будет немедленно принята к обслуживанию. Представляется вполне естественным, что при организации работы той или иной системы массового обслуживания следует стремиться к сокращению среднего числа заявок, находящихся в очереди, к сокращению времени ожидания при обслуживании.
Системы с отказами. Простейший тип системы массового обслуживания – одноканальная система с отказами. В качестве примера такой системы можно указать систему, состоящую из одной телефонной линии, или детектор частиц, состоящий из одного счетчика Гейгера – Мюллера. Граф состояний рассматриваемой системы показан на рисунке 5.1.
 |
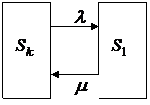Рисунок 5.1. – Граф состояний простейшего типа системы массового обслуживания
Здесь состояние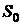 
– канал свободен, состояние 
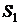– канал занят. Через 
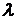обозначена интенсивность потока заявок, а через 
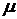– интенсивность потока обслуживаний. Этот граф состояний достаточно прост. Если система находится в состоянии 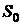, то поступающая на ее вход заявка переводит систему в состояние 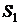, то есть начинается обслуживание. Как только обслуживание заканчивается, система возвращается в состояние 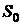и готова принять новую заявку.
Не останавливаясь подробнее на данном типе систем, перейдем к более общему случаю – n-канальной системе с отказами. Примером может служить система, состоящая из п телефонных линий. Именно такую систему рассматривал в свое время основатель теории массового обслуживания Эрланг. Соответствующий граф состояний дан на рисунке 5.2.
 |
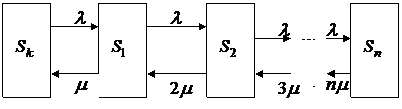Рисунок 5.2. – Граф состояний n-канальной системы с отказами
Для состояний системы использованы обозначения: 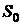– все каналы свободны, 
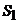– занят один канал, остальные свободны, 
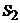– заняты два канала, остальные свободны, 
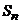– заняты все п каналов. Как и в предыдущем примере, 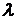–интенсивность потока заявок, 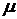–интенсивность потока обслуживаний.
Однокональная система с ограниченной очередью. Пусть ограничение осуществляется по числу заявок, стоящих в очереди; число мест в очереди равно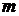 
. Если все места заняты, то очередная заявка, поступающая в систему, получает отказ. Примером подобной системы может служить автозаправочная станция, имеющая одну колонку (один канал обслуживания) и площадку, на которй могут находиться одновременно не более 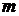автомашин. Если все места на площадке заняты, то очередная машина, прибывшая к станции, не останавливается, а проезжает мимо.
Граф состояний рассматриваемой системы показан на рисунке 5.3.
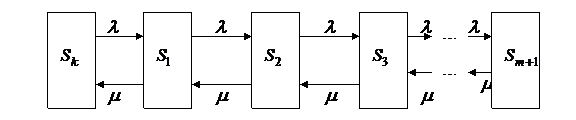
Рисунок 5.3. – Граф состояний одноканальной системы с ограниченной очередью
Здесь 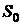– канал свободен, 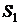– канал занят, 
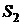– канал занят, одна заявка стоит в очереди, 
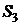– канал занят, в очереди стоят две заявки.., 
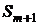– канал занят, в очереди стоят 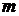заявок. Как обычно, 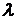–интенсивность потока заявок, 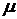–интенсивность потока обслуживаний.
Одноканальная система с неограниченной очередью. Заметим, что такие системы массового обслуживания довольно часто встречаются на практике: врач, принимающий больных, телефон-автомат с одной будкой, порт с одним причалом, где выгружаются прибывающие суда и т.д. Граф состояний рассматриваемой системы представлен на рисунке 5.4.
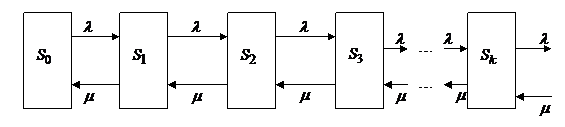
Рисунок 5.4. – Граф состояний одноканальной системы с неограниченной очередью
Здесь 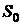– канал свободен, 
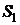– канал занят, 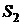– канал занят, в очереди стоит одна заявка, 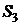– канал занят, в очереди стоят две заявки.., 
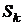– канал занят, в очереди стоят 
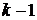заявок… и т.д.
Ранее рассматривались графы с конечным числом состояний. Здесь же мы встречаемся с системой, характеризующейся бесконечным числом дискретных состояний.
Пример модели простейшей системы.
Вероятность поступления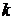 
вызовов за время 
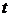для закона распределения Пуассона определяется по следующей формуле:
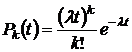, (5.1)
где 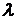– интенсивность случайного потока, т.е. среднее число поступающих заявок в единицу времени.
Временной интервал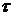 
между заявками в простейшем потоке подчиняется экспоненциальному закону распределения:
, 
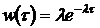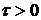. (5.2)
Предположим, что длительность обслуживания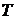 
заявки также подчиняется экспоненциальному закону распределения:
, 
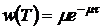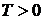, (5.3)
где 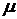– интенсивность обслуживания, т.е. среднее число обслуженных заявок в единицу времени.
Рисунок 5.5. – Схема имитационной модели простейшей системы массового обслуживанияч