Практические приемы подбора кривых

Подбор подходящих уравнений для поверхности отклика в подавляющем большинстве случаев можно произвести без со­ставления и решения нормальных уравнений типа (1.90) в общем виде. С этой целью можно воспользоваться готовыми фор­мулами. Наиболее характерные формулы и примеры их прак­тического использования, заимствованные из [23], рассмотрены ниже.

Линейная аппроксимация в случае двух переменных.Пусть даны N пар точек х_i и у_i, приближенно представляющих зависи­мость

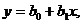(1.93)

где b₀ - отрезок, отсекаемый данной прямой на оси y, a b₁ - уг­ловой коэффициент этой прямой.

Коэффициенты b₀ и b₁ оцениваются из следующих уравнений

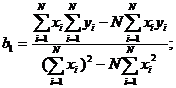(1.94)

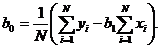(1.95)

Пример. Найти уравнение прямой, аппроксимирующей следующее множество точек:

x	2,0	4,0	6,0	8,0	10,0
y	5,5	6,3	7,2	8,0	8,6

Решение. Пусть уравнение прямой есть 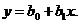Для вычисления коэф­фициентов согласно формулам (1.94), (1.95) находим следующие значения:

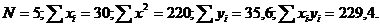
Подставляя эти значения в (1.94) и (1.95), находим:

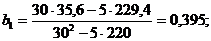
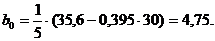
Таким образом, искомое уравнение есть y = 4,75+0,395x.

Линейная аппроксимация в случае многих переменных.Исполь­зуем линейную форму для определения соотношения между пере­менной у и несколькими другими переменными х₁, x₂, х₃, ..., х_n, записав ее в виде

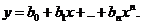(1.96)

Коэффициенты регрессии b₀, b_t, b₂, ..., b_n находят из следу­ющих уравнений, связывающих отклонения каждой из величин от их математических ожиданий:

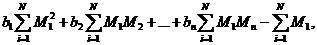
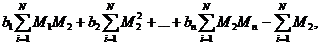
(1.97)

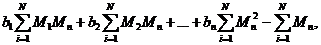
Здесь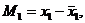

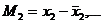
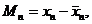
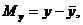
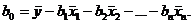
Нелинейная аппроксимация.Между двумя переменными мо­жет существовать простая зависимость вида

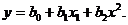(1.98)

Коэффициенты этого уравнения b₀, b₁, b_sоценивают на основа­нии уравнений

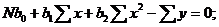
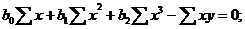(1.99)

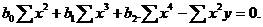
Пример. Определить уравнение вида y = b₀+b₁ x+ b₂ x², аппроксимиру­ющее следующее множество точек:

x	2,00	4,00	6,00	8,00	10,00	12,00	14,00
y	3,76	4,44	5,04	5,56	6,00	6,36	6,64

Решение. Вычисляя коэффициенты согласно уравнениям (1.99), найдем:

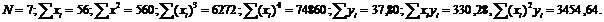
Подставляя эти значения в соотношения (1.99), получим уравнения:

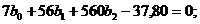
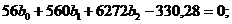
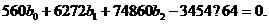
Решая их, определяем b₀ = 3,0; b₁ = 0,4; b₂ = - 0,01. Искомое уравнение имеет вид

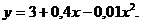
Логарифмическая аппроксимация. Будем отыскивать связь между переменными х, у в виде

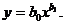(1.100)

Коэффициенты b₀ и b₁ находят из уравнений:

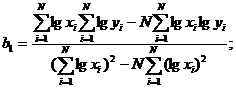
(1.101)

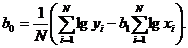
Пример. Необходимо аппроксимировать следующее множество точек логарифмической кривой вида (1.100):

x
y

Решение. Воспользуемся выражениями (1.101), для которых при N=6 вычис­ляем:

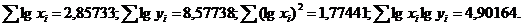
Подставляя эти выражения в соответствующие уравнения, находим

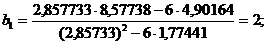
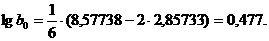
Таким образом, уравнение, соответствующее заданному множеству точек, есть y=3x², где 3 – антилогарифм числа 0,477.

Экспоненциальная аппроксимация.Простейшая экспоненциальная зависимость двух переменных записывается в виде

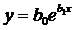. (1.102)

Коэффициенты b₀ и b₁ определяются из уравнений:

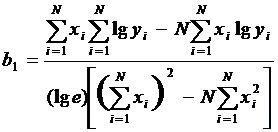
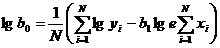(1.103)

где lg e =0,4343.

Один из простых видов экспоненциальной зависимости может быть записан также в форме

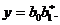(1.104)

Оценки параметров b₀ и b₁ эти зависимости могут быть определе­ны из уравнений

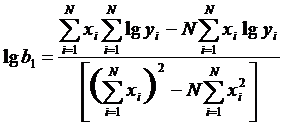
(1.105)

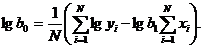
Для графического определения типа уравнения наилучшего приближения и значений его коэффициентов строят график по множеству заданных точек, наносимых на бумагу с логарифмичес­кой, полулогарифмической или обыч­ной прямоугольной системой коорди­нат. Линейный характер графика в ка­кой-либо из перечисленных систем ко­ординат говорит об определенном типе аппроксимирующей зависимости.

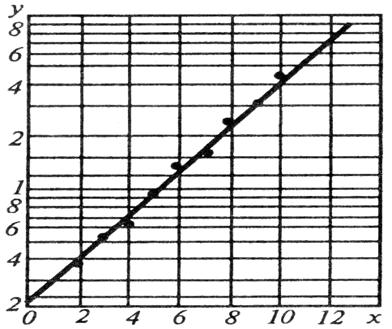
Рис. 1.26. К примеру.

При необходимости нелинейную функцию можно предварительно при­вести к линейному виду путем соответствующего преобразования (или разложения в ряд), в ча­стности:

для дробно-линейной зависимости

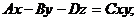(1.106)

для экспоненциальной зависимости

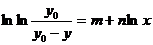(1.107)

или

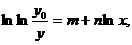(1.108)

где т, ln а и п - постоянные величины;

для тригонометрической зависимости

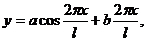(1.109)

где а = A sin α; b =A cos α.

Соответствие между различными системами координат и ти­пами уравнений, изображающимися в них прямой линией, следу­ющее:

Система координат	Вид уравнения
Прямоугольная декартова	у=b0+b1 x
Полулогарифмическая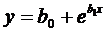
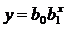Логарифмическая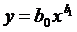
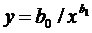
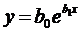