Множественная линейная модель. Методы уменьшения мультиколлениарности.

Исключение переменной из модели.Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных. Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. В эконометрических моделях, применяемых в прикладных целях, желательно не исключать объясняющую переменную до тех пор, пока мультиколлинеарность не станет серьезной проблемой.

Получение дополнительных данных или новой выборки. Возможно, для уменьшения мультиколлинеарности достаточно увеличить объем выборки. Это сократит дисперсии коэффициентов регрессии и тем самым увеличит их статистическую значимость.

Изменение спецификации модели. Иногда проблема мультиколлинеарности может быть решена путем изменения спецификации модели.

Использование предварительной информации о некоторых параметрах. Возможно, что значения коэффициентов, рассчитанные для каких-либо предварительных моделей, или для аналогичной модели по ранее полученной выборке, могут быть использованы для исследуемой в данный момент модели.

Преобразование переменных. Иногда минимизировать либо вообще устранить проблему мультиколлинеарности можно с помощью преобразования переменных: разделив все переменные уравнения множественной регрессии на одну из коррелирующих переменных.

Нелинейная регрессия. Виды моделей. Примеры.

1) Логарифмические (лог-линейные) модели. Предположим, экономическая зависимость моделируется формулой Y=A 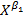, где А и 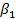- параметры модели (т.е. константы, подлежащие определению). Фунция Y=A 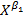может отражать зависимость спроса 𝑌 на изучаемое благо от его цены X (𝛽₁ < 0) или от дохода X (𝛽₁ > 0). При такой интерпретации переменных X и 𝑌 функция Y=A 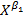называется функцией Энгеля.

2) Полулогарифмические модели - модели вида 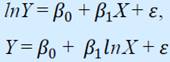(8,12)

Такие модели обычно используют в тех случаях, когда необходимо определять темп роста или прироста каких-либо экономических показателей.

-- Лог-линейная модель. Рассмотрим зависимость, хорошо известную в финансовом анализе 𝑌_𝑡=𝑌₀(1+𝑟)^𝑡 , где Y₀ — начальная величина переменной Y (например, первоначальный вклад в банке); 𝑟 — сложный темп прироста величины Y (процентная ставка и инфляция); Yt — значение величины Y в момент времени t (вклад в банке в момент времени t). Модель (8.12) легко сводится к полулогарифмической модели (8.10). Действительно, прологарифмировав имеем: lnYt = lnY₀ + tln(1 + r).

-- Линейно-логарифмическая модель .Рассмотрим так называемую линейно-логарифмическую модель Y = 𝛽0 + 𝛽₁lnX + 𝜀.Она сводится к линейной модели заменой Х*= lnХ. В данной модели коэффициент 𝛽₁ определяет изменение переменной Y вследствие единичного относительного прироста X (например, на 1%), т.е. характеризует отношение абсолютного изменения Y к относительному изменению X.

3) Обратная модель - модель вида Y=𝑌=𝛽₀+𝛽₁∙ +𝜀. Эта модель сводится к линейной заменой Х*= 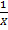. Данная модель обычно применяется в тех случаях, когда неограниченное увеличение объясняющей переменной X асимптотически приближает зависимую переменную Y к некоторому пределу (в данном случае к 𝛽₀.

4) Степенная модель. Степенная функция вида 𝑌=𝛽₀+𝛽₁𝑋+𝛽₂𝑋²+⋯+𝛽_𝑚𝑋^𝑚+𝜀 часто отражает ту или иную экономическую зависимость

5) Показательная модель Показательная функция вида 𝑌=𝛽₀𝑒^𝛽₁^𝑋 также достаточно широко применяется в эконометрическом анализе (здесь е 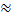2,7). Наиболее важным ее приложением является ситуация, когда анализируется изменение переменной Y с постоянным темпом прироста во времени. В этом случае переменная X символически заменяется переменной t: 𝑌=𝑏₀𝑒^𝛽₁^{𝑡 .} Данная функция путем логарифмирования (lne^𝛽₁^𝑡 = β₁t) сводится к лог-линейной модели 𝑙𝑛𝑌=𝑙𝑛𝛽₀+𝛽₁𝑡.