Множественная линейная регрессия. Проблема мультиколлениарности.
Мультиколлинеарностью называется высокая степень коррелированности двух или нескольких объясняющих переменных в уравнении множественной регрессии. Крайним случаем мультиколлинеарности является линейная зависимость между объясняющими переменными. Считается, что две переменные  и
и 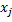 сильно коррелированны, если выборочный коэффициент корреляции двух объясняющих переменных
сильно коррелированны, если выборочный коэффициент корреляции двух объясняющих переменных 
Поясним. Пусть имеется m объясняющих факторов:X1, X2, …..Xm. Матрица межфакторной корреляции состоит из парных коэффициентов корреляции и имеет вид:

Парный коэффициент корреляции 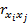 определяется по формуле
определяется по формуле
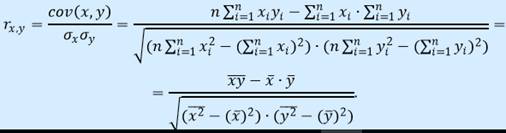
Отметим, так как 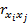 =1, (i=1,2,…m) и
=1, (i=1,2,…m) и 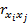 =
=  , то данная матрица является симметрической. Если связь между факторами полностью отсутствует, то недиагональные элементы матрицы межфакторной корреляции будут равны нулю, а ее определитель будет равен единице:
, то данная матрица является симметрической. Если связь между факторами полностью отсутствует, то недиагональные элементы матрицы межфакторной корреляции будут равны нулю, а ее определитель будет равен единице: 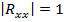
Последствия мультиколлинеарности:
Выделим следующие последствия мультиколлинеарности:
1. Большие дисперсии (стандартные ошибки) оценок коэффициентов уравнения множественной регрессии. Это расширяет интервальные оценки, ухудшая их точность. Последнее затрудняет нахождение истинных значений оценок коэффициентов.
2. Уменьшаются t-статистики оценок. Оценки имеют малую статистическую значимость, в то время как модель в целом является значимой (имеет высокое значение коэффициент детерминации  ).
).
3. Оценки коэффициентов уравнения по МНК и их стандартные ошибки становятся очень чувствительными к малейшим изменениям данных. Оценки коэффициентов становятся неустойчивыми.
4. Затрудняется определение доли вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной.
5. Возможно получение неверного знака у коэффициента регрессии.
15. Множественная линейная модель. Методы определения мультиколлининеарности.
Определение мультиколлинеарности
Существует несколько признаков, по которым может быть установлено наличие мультиколлинеарности.
1. Коэффициент детерминации  достаточно высок, но некоторые из коэффициентов уравнения множественной линейной регрессии статистически незначимы (имеют низкие t-статистики).
достаточно высок, но некоторые из коэффициентов уравнения множественной линейной регрессии статистически незначимы (имеют низкие t-статистики).
2. Высокая корреляция в уравнении регрессии с двумя объясняющими переменными. Если объясняющих переменных больше двух целесообразнее использовать частные коэффициенты корреляции.
Частным коэффициентом корреляции называется коэффициент корреляции между двумя объясняющими переменными, очищенный от влияния других переменных. Например, при трех объясняющих переменных Х1, Х2, Х3 частный коэффициент корреляции между Х1 и Х3, очищенный от Х2, рассчитывается по формуле
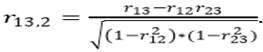 Замечание: частный коэффициент корреляции может существенно отличаться от «обычного» коэффициента корреляции. Для более обоснованного вывода о корреляции между парами объясняющих переменных необходимо рассчитывать все частные коэффициенты корреляции.
Замечание: частный коэффициент корреляции может существенно отличаться от «обычного» коэффициента корреляции. Для более обоснованного вывода о корреляции между парами объясняющих переменных необходимо рассчитывать все частные коэффициенты корреляции.
3. Сильная регрессия между объясняющими переменными. Какая-либо из объясняющих переменных является комбинацией других объясняющих переменных (линейной или близкой к линейной).
