Линейныеоднофакторные модели регрессии

Рассматривается связь результативного признака yс одним признаком фактором x. Для выявления меры такой связи, прежде всего, рассчитывается коэффициент 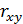. Обычно цель расчета состоит в том можно ли считать связь линейной.

Линейный коэффициент корреляции представляет собой среднюю величину из произведений нормированных отклонений для x и y:

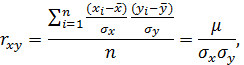
где 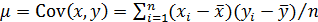– ковариация признаков x и y. 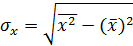, 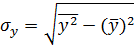. После несложных преобразований можно получить следующее представление коэффициента корреляции:

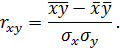
Свойства коэффициентов парной корреляции

1)

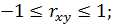
2) Если 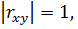то между случайными величинами x и y существует функциональная линейная зависимость: при 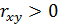– прямая (положительная); при 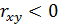– обратная (отрицательная).

3) Если 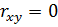, то это говорит лишь об отсутствии линейной зависимости между x и y, но не вообще об отсутствии корреляционной связи.

При 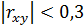связь считается слабой, 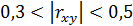– умеренной, при 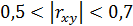– заметной, 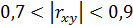– тесной, при 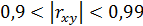– весьма тесной. Коэффициент парной корреляции обладает свойством симметрии: .

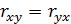Метод наименьших квадратов

Пусть задана двумерная случайная величина 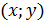, где x и y– зависимы. Нанесем на координатную плоскость 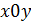точки: 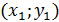, ,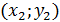…, , 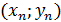являющиеся значениями случайной величины в n испытаниях. Нанесенное на координатную плоскость множество точек, называется корреляционным облаком.

Функцияf(x)называется наилучшей аппроксимацией зависимости y от x в смысле метода наименьших квадратов (МНК), если математическое ожидание 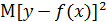принимает наименьшее возможное значение. Здесь y выступает как случайная величина, а 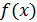– неслучайная аналитическая функция.

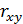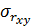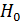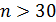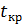Сформулируем два важнейших (но не единственных) условия применимости МНК. Первое, объем выборки nдолжен быть таким, чтобы величина коэффициента корреляции превосходила его среднюю ошибку не менее чем в t раз, где t – критерий Стьюдента при вероятности нулевой гипотезы об отсутствии корреляции на уровне значимости α. При этом, если , то полагают равным 2. Если 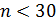, то 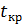определяют по таблице, полагая число степеней свободы равным 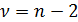. Второе, распределение ошибки ε случайной величины y, зависящей от неслучайной величины x должно быть близко к нормальному закону.

Обычно визуально по корреляционному облаку предполагают вид функциональной зависимости y от x. Уравнение взаимосвязи двух переменных можно представить в виде: 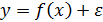, где ε – случайная ошибка, фактическое распределение значений которой неизвестно.

Свойства параметров регрессионной модели 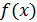зависят от свойств случайной составляющей. Для того, чтобы можно было применять МНК относительно ошибки ε должны быть сделаны дополнительные предположения.

Предпосылки МНК

Требования, предъявляемые к случайной величине ε, носят фундаментальный характер и заключаются в выполнении ряда условий.

1) Математическое ожидание значений остатков равно 0, т.е. 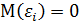, говоря точнее, должно выполняться 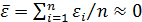. Это требование гарантирует несмещенность оценок параметров регрессии. Оно практически выполняется при непосредственной реализации МНК. Если оценки несмещенные, то их можно сравнивать по разным выборкам, что практически очень важно.

2) Величины остатков 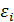при каждом последовательном измерении имеют случайный характер. Т.е. 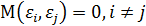, а нулевая средняя величина остатков не зависит от .

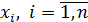3) Дисперсия остатков 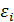не зависит от 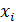и постоянна, т.е. 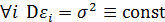. При каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, но не должно быть некоторой постоянной причины, вызывающей большую ошибку. Это требование называется условием равноизменчивости или гомоскедастичности. Его выполнение гарантирует эффективность оценок параметров регрессии, что позволяет (при выполнении предыдущих условий) включать в модель дополнительно новые значения переменных наблюдения 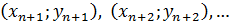с целью повышения точности модели. Гомоскедастичность позволяет проводить интервальные оценки. Нарушение гомоскедастичности называется гетероскедастичностью.

4) Значения остатков распределены независимо друг от друга. Фактически это означает отсутствие автокорреляции, более свойственной динамическим рядам.

При выполнении сформулированных четырех условий, можно при необходимости увеличивать объем выборки и тем самым повышать состоятельность оценок.

5) При условии выполнения пунктов 1)-3) еще необходимо, чтобы 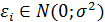, т.е. остатки были распределены по нормальному закону или близкому к нему. Это условие не выполняется для малых выборок, но достаточно хорошо корректируется статистиками 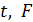– Стьюдента и Фишера, которые позволяют оценить значимость, исследуемых характеристик.

Проблема однако в том, что предпосылки МНК могут быть проверены только после того как с его помощью получено уравнение регрессии. Кроме выдвинутых пяти предпосылок МНК, следует добавить еще одну: для линейной множественной регрессии количество наблюдений n должно превышать количество коэффициентов k при переменных модели не менее чем в 7-8 раз, т.е. 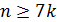(эмпирический факт). Например, если 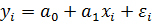, то требуется не менее 8 наблюдений. Если вид теоретической функции регрессии усложняется, то это требует увеличения числа наблюдений. Так, для 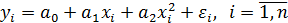требуется уже не менее 14 наблюдений.