Содержательный модуль: Механика сетей.

Тема ГЕОМЕТРИЯ И СТАТИКА РЫБОЛОВНЫХ СЕТЕЙ

Геометрия рыболовных сетей.

Форма ячеи натянутой сети определяется поса­дочными коэффициентами. Посадочным коэффи­циентом называют соотношение длины каната L, на которую са­жается сеть, и длины сажаемой сетной кромки в жгуте L0. uX=L/L0 (5.1) Аналогично по боковой кромке:uY=H/H0 (5.2) Посадочные коэффициенты связаны между собой зависимостью: uX2+ uY2=1(5.3)

При линейных деформациях прямоугольной сети связь между приращениями высоты и длины сети, вызванными линейными деформациями, имеет вид.

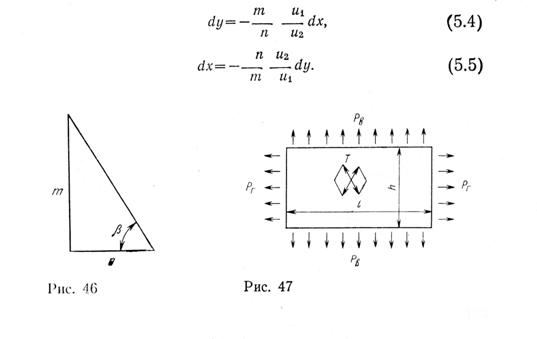
Если прямоугольная сеть посажена с разными посадочными коэффициентами по верхней и нижней подборам, то она примет форму части кругового кольца, а ее высота определяется по формуле

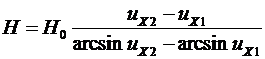(5.6)

Коэффициент посадки и_Х соответствующий заданной углом bформе клиновидной сети (рис. 46), рассчитывается по формуле

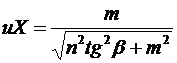(5.7)

Статика плоской рыболовной сети. Если к горизонтальным кромкам плоской прямоугольной сети приложены вертикальные растягивающие нагрузки Р_В (рис. 47), то для того чтобы сеть сохранила форму прямоугольника, к ее вертикальным кромкам должны быть приложены соответствующие по величине горизонтальные растягивающие усилия Р_г. Связь между вертикальными и горизонтальными усилиями имеет вид

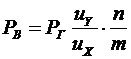(5.8)

Растягивающая нагрузка, приходящаяся на единицу длины кромки сети, называется напряжением и обозначается

s₁=Р_Г/h= s₁= Р_B/1.(5.9)

Напряжения связаны между собой выражением

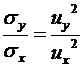(5.9а)

Под действием нагрузок, приложенных к кромкам сети, в ее нитях возникают натяжения Г, вычисляемые по формулам:

T=s_y·a·tga, (5.10)

T = s_x·a·ctga. (5.11)

Если помимо нагрузок по горизонтальным и вертикальным кромкам сети в ее плоскости действуют равномерно распределенные силы q (сила тяжести или гидродинамического сопротивления), то напряжения в каждой точке сети определяются по фор­мулам:

s₂=qy+s₂₀ (5.12)

s₁=(qy+s₂₀)tg²a. (5.13)

Такая сеть находится всиловом поле s₂ и s₁. Линии уровня у = const совпадают в рассматриваемом случае с горизонтальными диагоналями ячей, а градиент поля — с вертикальными диагоналями (х=const).

Литература: [1], стр. 75-92.

Пояснение по решению задач.

Задача 5.5

Приращение высоты сети определяется по формуле 5.4

Задача 5.6

Задача решается по формулам 5.4, 5.5

Задача 5.7

Задача решается по формуле 5.6

Задача 5.17

Задача решается по формуле 5.7

Задача 5.19

Задача решается по формулам 5.9- 5.11,учитывая, что u_X=sin(a) и u_Y=cos(a).

Вопросы для самоконтроля

1. Какую форму принимает сетное полотно, посаженое с разными коэффициентами по верхней и нижней подборе?

2. Какова зависимость между горизонтальным и вертикальным посадочными коэффициентами?

3. Как определяется натяжение в сети при её линейной деформации?

Содержательный модуль:

Внешние силы, действующие на орудия лова.