Понятие первообразной и неопределенный интеграл

Определение. Функция 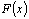называется первообразной функцией для функции 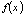на промежутке 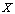, если в каждой точке этого промежутка .

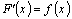Пример. 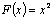является первообразной для 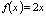, т.к. .

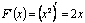Можно заметить, что если для функции 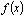существует первообразная 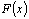, то она не является единственной. Возвращаясь к примеру, видно, что и функции 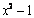, 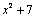и вообще 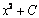( 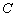- некоторое число) являются первообразными для функции 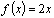. Таким образом можно сформулировать следующую теорему.

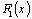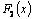Теорема.Если и - первообразные для функции 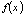на некотором промежутке 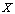, то найдется такое число 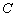, что будет справедливо равенство:

.

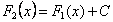Из данной теоремы следует, что, если 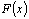- первообразная для функции 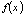, то выражение вида 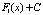, где 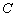- произвольное число, задает все возможные первообразные для .

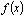Определение. Совокупность всех первообразных функции 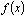на промежутке 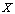называется неопределенным интегралом от функции 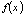и обозначается 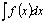, где 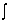- знак интеграла, 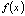- подынтегральная функция, 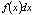- подынтегральное выражение.

Таким образом:

,

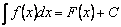где 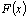- некоторая первообразная для 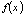, 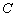произвольная постоянная.

Определение. Операция нахождения неопределенного интеграла называется интегрированием этой функции.

Свойства неопределенного интеграла

1)Производная от неопределенного интеграла равна подынтегральной функции, т.е. .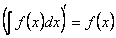

□ Доказательство.Дифференцируя левую и правую части равенства 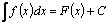, получаем: .■

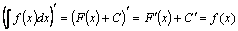2)Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. .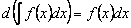

□ Доказательство.По определению дифференциала и свойству 1 имеем: ■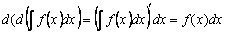

3)Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .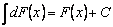

□ Доказательство.Рассматривая функцию 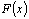как первообразную для некоторой функции 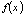, можно записать: 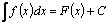и на основании 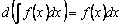дифференциал неопределенного интеграла 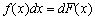, откуда .■

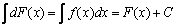4)Постоянный множитель можно выносить за знак интеграла, т.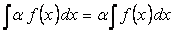е. , где 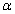- некоторое число.

5)Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .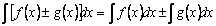

Некоторые табличные интегралы

,
,			,

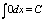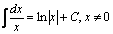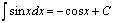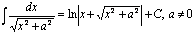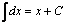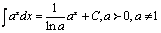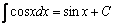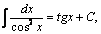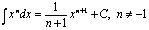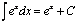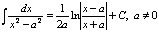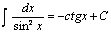Пример.Найти .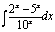

Решение.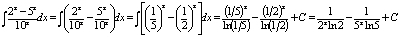

Пример.Найти .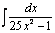

Решение. = .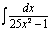

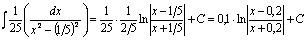Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.

Теорема.

Пусть функци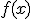и и 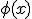определены соответственно на промежутках 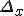и 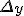, причем 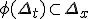. Если функция 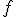имеет на 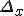первообразную 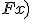и, следовательно,

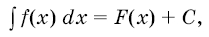(1)

а функция 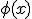дифференцируема на 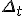, то функция 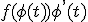имеет на 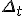, первообразную 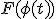и

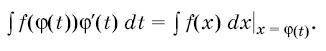(2)

Формула (1) называется формулой интегрирования подстановкой, а именно подстановкой 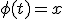. Это название объясняется тем, что если формулу (2) записать в виде

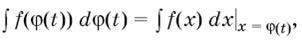
то будет видно, что, для того чтобы вычислить интеграл 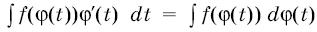), можно сделать подстановку 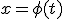, вычислить интеграл 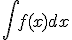и затем вернуться к переменной 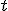, положив .

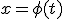Теорема 1. Пусть f(z) - непрерывная функция, заданная на промежутке [p, q], а φ(x) - непрерывная функция, заданная на промежутке [a, b], имеющая там непрерывную же производную φ'(x) и удовлетворяющая неравенству p ≤ φ(x) ≤ q.

В таком случае

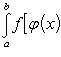
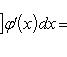
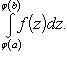(22)

Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.

Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.

36. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.

Неопределенный интеграл

Рассмотрим дифференцируемые функции переменной

U=U(x) и V=V(x)

Т.к. d(uv) = (uv)’dx=u’vdx+uv’dx= du*v+u*dv, то проинтегрируем по переменной х это равенство и учтем, что интеграл суммы функции – это сумма интегралов

⌠d(uv)= ⌠vdu+⌠udv

uv=⌠vdu+⌠udv

Метод интегрирования по частям применяется, когда нельзя вычесть интеграл методом замены переменной.

Пример.

⌠lnx*x⁸dx = {u=lnx;dv= x⁸dx; du = 1/8dx; v= ⌠ x⁸dx= x⁹/9}=lnx* x⁹/9-⌠ x⁹/9-1/xdv=lnx* x⁹/9-1/9⌠ x⁸dx=lnx* x⁹/9-1/9* x⁹/9+C

Определенный интеграл.

^b⌠udv=(uv-⌠vdu)^b│

^{a a}

u=u(x), v=v(x)

^b⌠udv=uv^b│-⌠ ^b vdu

^{a a a}