Арксинус, арккосинус, арктангенс, арккотангенс.
Определения обратных тригонометрических функций и их основные свойства приведены в одноимённом разделе в главе «Тригонометрия». Поэтому здесь мы oграничимся лишь короткими комментариями, касающимися их графиков, полученных поворотом графиков тригонометрических функций вокруг биссектрисы 1-го координатного угла.
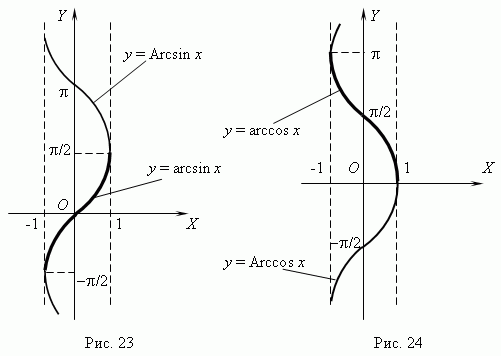
Функции y = arcsin x ( рис.23 ) и y = arccos x ( рис.24 ) многозначные, неограниченные; их область определения и область значений соответственно: -1 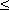 x
x  +1 и -
+1 и -  < y < +
< y < + 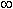 . Поскольку эти функции многозначные, не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
. Поскольку эти функции многозначные, не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: -1 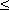 x
x 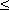 +1 ;
+1 ;
их области значений: -  /2
/2 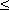 y
y 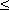
 /2 для y = arcsin x и 0
/2 для y = arcsin x и 0  y
y 
 для y = arccos x;
для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и x = 1 у функции y = arccos x).
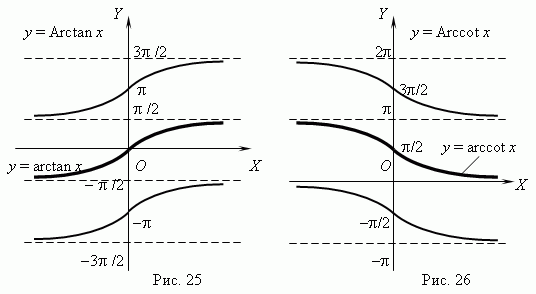
Функции y = Arctg x ( рис.25 ) и y = Arcctg x ( рис.26 ) - многозначные, неограниченные функции; их область определения: - 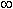
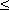 x
x 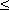 +
+ 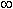 . Их главные значения y = arctg x и y = arcctg x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
. Их главные значения y = arctg x и y = arcctg x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
Функции y = Arctg x и y = Arcctg x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: - 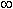
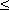 x
x 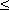 +
+ 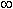 ;
;
их области значений: -  /2 < y <
/2 < y <  /2 для y = Arcctg x и 0 < y <
/2 для y = Arcctg x и 0 < y <  для y = arccos x;
для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные ( y= Arctg x – возрастающая функция; y = arcctg x – убывающая );
- только функция y = arctg x имеет единственный ноль ( x = 0 ); функция y = arcctg x нулей не имеет.
Способы задания функции
1) словесный способ (правило задания функции описывается словами)
2) табличный (задание функции с помощью таблицы, в которой указаны значения функции)
3) графический (задание функции с помощью графика)
4) аналитический (задание функции с помощью формул)
Что значит прочитать график? Значит - назвать свойства функции.
Свойства функции
1.область определения Д (f)
2.у=0; у>0; у<0
3. унаиб ; унаим
4.возрастание, убывание
5.непрерывность
6.ограниченность
7.выпуклость
8.четность
9.область значений функции Е(f) )
| Функция | Область определения | Множество значений | ||
| y = ax + b | x Î R | y Î R | ||
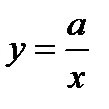 | x ¹ 0 | y ¹ 0 | ||
| y = ½x½ | x Î R | y ³ 0 | ||
| y = x2 | x Î R | y ³ 0 | ||
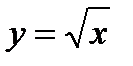 | x ³ 0 | y ³ 0 | ||
| y = ax | x Î R | y > 0 | ||
| y = logax | x > 0 | y Î R | ||
| y = logxa | x > 0, x ¹ 1 | y Î R | ||
| Функция | Условие | |||
 | f(x) ¹ 0 | |||
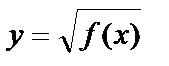 | f(x) ³ 0 | |||
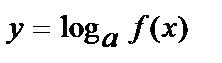 | f(x) > 0 | |||
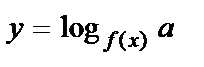 | f(x) ¹ 1 f(x) > 0 | |||
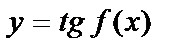 | f(x) ¹ p/2 + pт | |||
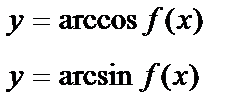 | -1 £ f(x) £ 1 | |||
Примеры.
. Постройте график.
 х2-1, если -2≤ х ≤2;
х2-1, если -2≤ х ≤2;
у = 2-х, если х 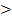 2;
2;
х+2, если х 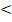 2
2
Графиком функции у=  х2-1 является парабола, ветви которой направлены вверх (а=
х2-1 является парабола, ветви которой направлены вверх (а=  >0)
>0)
| х | -1 | -2 | ||||
| у | - 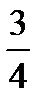 | -1 | - 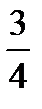 |
у=2-х
| х | 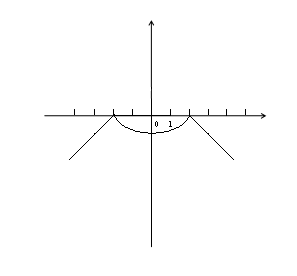 2 2 | |
| у |
у=х+2 у
| х | ||
| у |
х
1)Д(f): х 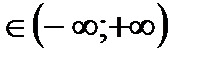
2)у=0 при х= 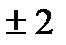
3)у>0 не существует
у<0 при х 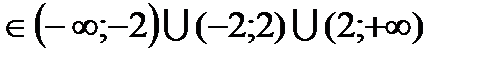
4)унаиб=0 при х=2 и х=-2
унаим- не существует
5)f(х) возрастает при х 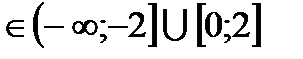
f(х) убывает при х 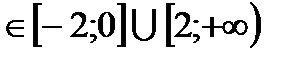
6)функция непрерывна
7)ограничена сверху осью Ох
8)выпукла вниз при х 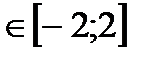
9)функция четная
10)Е(f): у 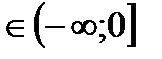
Решить самостоятельно.
1. При каком из указанных значений х выражение 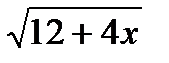 не имеет смысла?
не имеет смысла?
1)х=0 2)х= -1 3)х= -3 4)х= -5
2.Для каждого графика укажите соответствующую формулу:
у
| 0 1 |
| 1 1 1 |
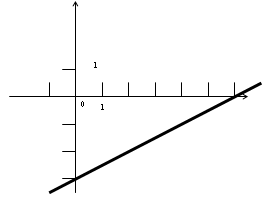 А) у Б)
А) у Б) х х
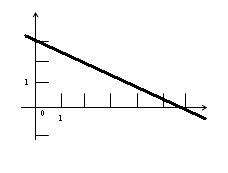 у
у
В) х
1)у=0,5х-3 2)у=-0,5х-3 3)у=-0,5х+3 4)у=0,5х+3
3.Как называется функция, график которой изображен на рисунке?
4.Какая функция является возрастающей? От чего это зависит?
5. Какая функция является убывающей?
6. Построить график функции у = - (х-2)2 и прочитать его (исследовать)
7. Сколько решений имеет система уравнений 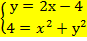 ? Решить графически.
? Решить графически.
8.Укажите систему уравнений, которая не имеет решений
а) 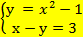 б)
б) 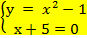 в)
в) 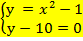 г) Все три системы
г) Все три системы
9.Решить систему: 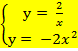
10. Решить неравенство  > -2х2 (по предыдущему чертежу)
> -2х2 (по предыдущему чертежу)
На каком промежутке график функции у=  лежит выше графика функции у= -2х2?
лежит выше графика функции у= -2х2?
11.Найти область определения функции у= 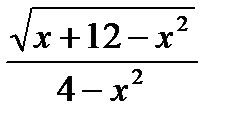
12.По формуле функции назовите ее график
1)у=  2)у=х3+2 3)у=2
2)у=х3+2 3)у=2 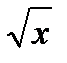 4)у= -8 5)х=2 6)у= -
4)у= -8 5)х=2 6)у= - 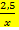 -1
-1
13. Задайте функцию графически:
у=х2+5; у=х2-3; у = (х-3)2 ; у = (х+2)2; у = (х+3)2-4
14.Найти наибольшее и наименьшее значения функции: а) у = 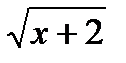 б) у= -х2+8х-12
б) у= -х2+8х-12
15. Постройте и прочитайте график функции у = 
Вопросы для самопроверки:
1. Способы задания функции.
2. Какие функции называются периодическими?
3. Как расположены графики взаимно-обратных функций.
4. Какие функции называются возрастающими?
5. Какие функции называются убывающими?
6. Какие функции называются монотонными?
7. Что такое функция?
8. Что такое область определения функции?
9. Что такое множество значений функции?
10. Какие функции называются чётными?
11. Какие функции называются нечётными?
12. Свойства графиков чётной и нечётной функций.
13. Какие функции называются обратными?
14. Назовите пары взаимно обратных функций.
15. Какие свойства различны у взаимно обратных функций?
16. Какие свойства одинаковы у взаимно обратных функций?
17. Назовите область определения: 1) обратной пропорциональности 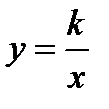 2) функции у=
2) функции у= 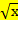
18. Что является графиком функции:
а)линейной у = кх+в б) прямой пропорциональности у=кх
в) квадратичной функции у = ах2+вх+с г) обратной пропорциональности у= 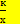
д) степенной функции у=х3 е) степенной у = 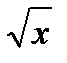
ж) модуль х
Форма контроля: проверка конспекта и устный опрос.
Самостоятельная работа № 12
