Тема 4.1. Функции и их свойства
Самостоятельная работа №11
Тема 4.1. Функции и их свойства
Самостоятельная работа (4 часа)
Цель: Выработать навык построения графиков элементарных функций, изучить взаимное расположение графиков обратных функций.
Линейная функция
y = kx + b, k – угловой коэффициент, b – свободный член
| y |
| x |
| xA |
| xB |
| yA |
| yB |
| B |
| A |
| a |
| y |
| x |
| y=2x |
| y=x |
| y=0,5x |
| y= -x |
Пусть y1 = k1x + b1 и y2 = k2x + b2. Тогда: 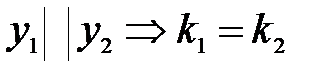 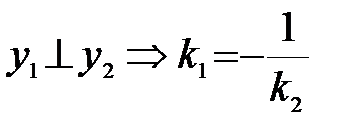 |
| y |
| x |
| y=2x |
| y=2x+5 |
| y=-0,5x+5 |
| y=-1 |
| -1 |
| -2 |
| x=-2 |
k = tga 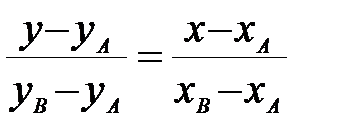 |
Пропорциональные величины. Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x ,
где k - постоянная величина ( коэффициент пропорциональности ).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол 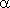 , тангенс которого равен k : tan
, тангенс которого равен k : tan 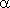 = k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика.
= k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика.
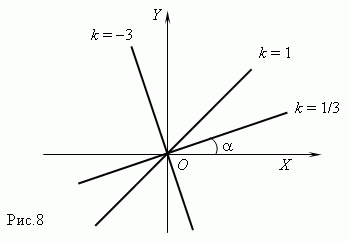 для k = 1/3, k = 1 и k = -3 .
для k = 1/3, k = 1 и k = -3 .
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C , где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9 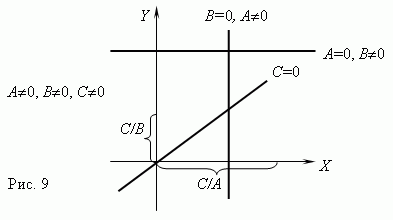
Квадратичная функция
Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a  0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат . Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат . Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в начале координат, а в точке с координатами: 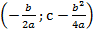 .
.
Форма и расположение в системе координат полностью зависит от двух параметров: коэффициента a при x2 и дискриминанта D: D = b2 – 4ac. Эти свойства следуют из анализа корней квадратного уравнения. Все возможные различные случаи для параболы показаны на рис.12. 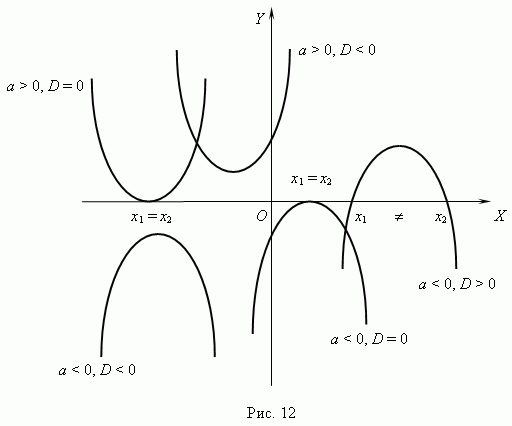
Основные характеристики и свойства параболы:
- область определения функции: - 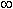 < x < +
< x < + 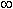 ( т.e. x
( т.e. x 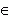 R ), а область значений: … ( ответьте, пожалуйста , на этот вопрос сами ! );
R ), а область значений: … ( ответьте, пожалуйста , на этот вопрос сами ! );
- функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная;
- функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая;
- при D < 0 не имеет нулей. ( А что при D 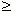 0 ? ) .
0 ? ) .
y = ax2 + bx + c, D = b2 – 4ac - дискриминант
| y |
| x |
| y=x2 |
| y=2x2 |
| y=0,5x2 |
M(x0,y0) – вершина параболы: 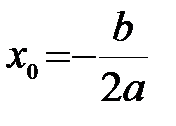 Уравнение параболы, проходящей через точку M: y = a(x – x0)2 + y0 x1, x2 – корни параболы: ax2 + bx + c = 0 Уравнение параболы, проходящей через точку M: y = a(x – x0)2 + y0 x1, x2 – корни параболы: ax2 + bx + c = 0 |
| y |
| x |
| a>0 D>0 |
| y |
| x |
| a<0 D=0 |
| y |
| x |
| a<0 D<0 |
| y |
| x |
| a<0 D>0 |
| y |
| x |
| a>0 D<0 |
| y |
| x |
| a>0 D=0 |
| y |
| x |
| x0 |
| x1 |
| x2 |
| y0 |
| M |
3.Обратная пропорциональность.Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x , где k - постоянная величина.
График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k. 
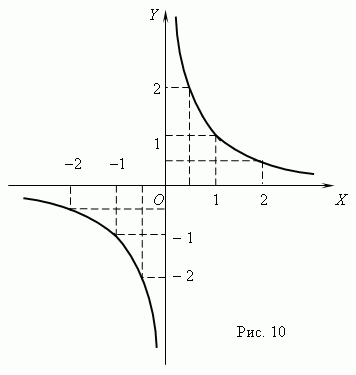
Основные характеристики и свойства гиперболы:
- область определения функции: x  0, область значений: y
0, область значений: y  0 ;
0 ;
- функция монотонная ( убывающая ) при x < 0 и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
4. Степенная функция. Это функция: y = axn, где a , n – постоянные.
При n = 1 получаем прямую пропорциональность: y = ax;
при n = 2 - квадратную параболу;
при n = -1 - обратную пропорциональность или гиперболу.
Таким образом, эти функции - частные случаи степенной функции.
Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно,
при n = 0 степенная функция превращается в постоянную величину: y = a, т.e. её график - прямая линия, параллельная оси Х, исключая начало координат (поясните, пожалуйста, почему ? ).
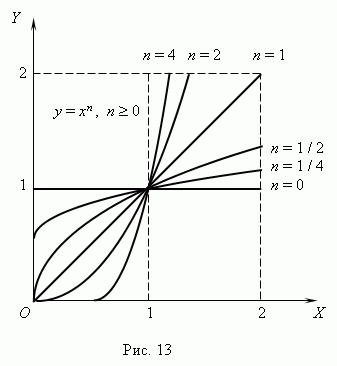
Все эти случаи ( при a = 1 ) показаны на рис.13 ( n 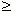 0 ) и рис.14 ( n < 0 ). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции: y =
0 ) и рис.14 ( n < 0 ). Отрицательные значения x здесь не рассматриваются, так как тогда некоторые функции: y = 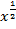 =
= 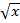 ; y =
; y = 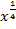 =
= 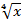 теряют смысл.
теряют смысл.
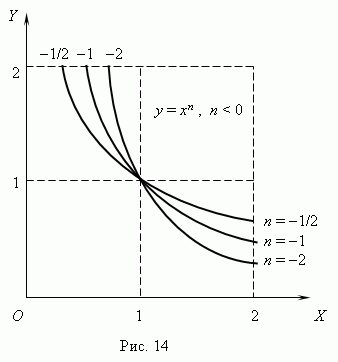
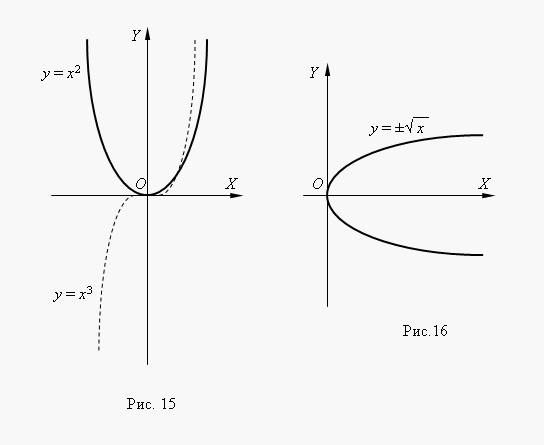
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3. При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой.
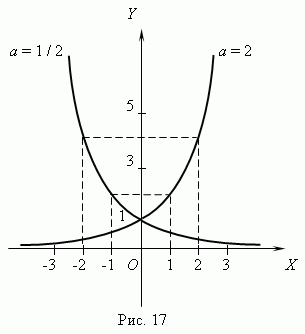
5.Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимает любые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает Основные характеристики и свойства показательной функции:
- область определения функции: - 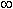 < x < +
< x < + 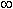 ( т.e. x
( т.e. x 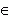 R );
R );
область значений: y > 0 ;
- функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- нулей функция не имеет.
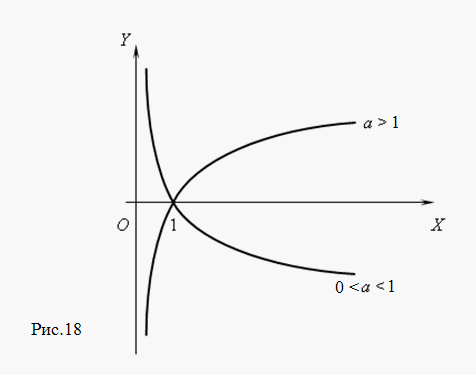
6.Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции:
- область определения функции: x > 0, а область значений: - 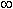 < y < +
< y < + 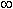 ( т.e. y
( т.e. y 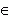 R );
R );
- это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
- у функции есть один ноль: x = 1.
7.Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y = sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой
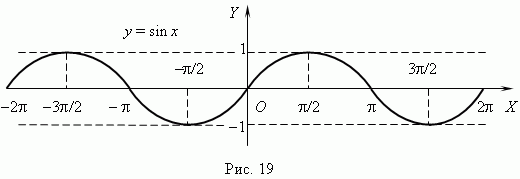
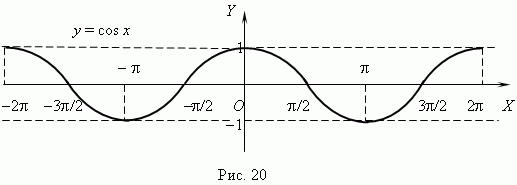
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на  /2.
/2.
Из этих графиков очевидны характеристики и свойства этих функций:
- область определения: - 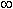 < x < +
< x < + 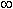 ; область значений: -1
; область значений: -1 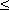 y
y 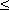 +1;
+1;
- эти функции периодические: их период 2  ;
;
- функции ограниченные ( | y | 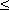 1 ), всюду непрерывные, не монотонные, но имеющие так называемые интервалы монотонности, внутри которых они ведут себя, как монотонные функции
1 ), всюду непрерывные, не монотонные, но имеющие так называемые интервалы монотонности, внутри которых они ведут себя, как монотонные функции
( см. графики рис.19 и рис.20 );
- функции имеют бесчисленное множество нулей.
Графики функций y = tgx и y = ctg x показаны соответственно на рис.21 и рис.22
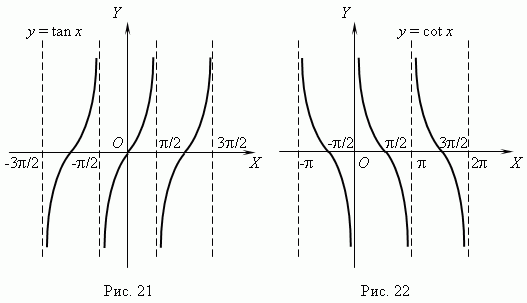
Из графиков видно, что эти функции: периодические ( их период  ), неограниченные, в целом не монотонные, но имеют интервалы монотонности ( какие? ), разрывные ( какие точки разрыва имеют эти функции? ). Область определения и область значений этих функций:
), неограниченные, в целом не монотонные, но имеют интервалы монотонности ( какие? ), разрывные ( какие точки разрыва имеют эти функции? ). Область определения и область значений этих функций:
y = tgx x≠  + πk y
+ πk y 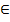 R
R
y = ctg x x≠ πk y 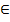 R
R
Примеры.
. Постройте график.
 х2-1, если -2≤ х ≤2;
х2-1, если -2≤ х ≤2;
у = 2-х, если х 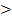 2;
2;
х+2, если х 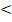 2
2
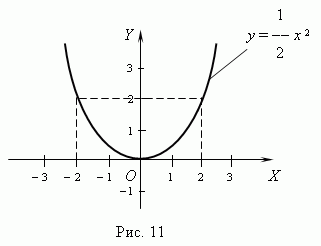
Графиком функции у=  х2-1 является парабола, ветви которой направлены вверх (а=
х2-1 является парабола, ветви которой направлены вверх (а=  >0)
>0)
| х | -1 | -2 | ||||
| у | - 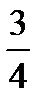 | -1 | - 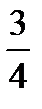 |
у=2-х
| х | 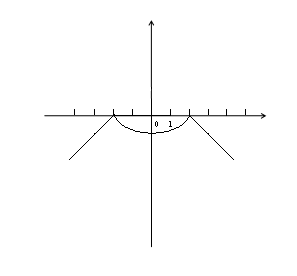 2 2 | |
| у |
у=х+2 у
| х | ||
| у |
х
1)Д(f): х 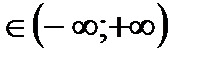
2)у=0 при х= 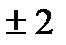
3)у>0 не существует
у<0 при х 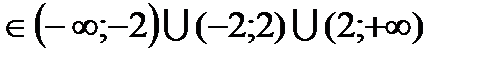
4)унаиб=0 при х=2 и х=-2
унаим- не существует
5)f(х) возрастает при х 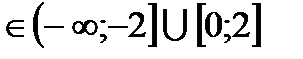
f(х) убывает при х 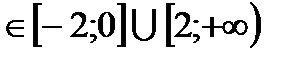
6)функция непрерывна
7)ограничена сверху осью Ох
8)выпукла вниз при х 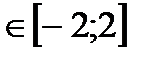
9)функция четная
10)Е(f): у 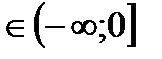
Решить самостоятельно.
1. При каком из указанных значений х выражение 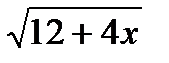 не имеет смысла?
не имеет смысла?
1)х=0 2)х= -1 3)х= -3 4)х= -5
2.Для каждого графика укажите соответствующую формулу:
у
| 0 1 |
| 1 1 1 |
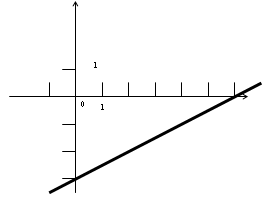 А) у Б)
А) у Б) х х
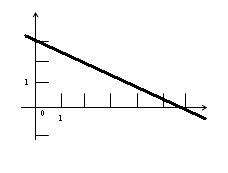 у
у
В) х
1)у=0,5х-3 2)у=-0,5х-3 3)у=-0,5х+3 4)у=0,5х+3
3.Как называется функция, график которой изображен на рисунке?
4.Какая функция является возрастающей? От чего это зависит?
5. Какая функция является убывающей?
6. Построить график функции у = - (х-2)2 и прочитать его (исследовать)
7. Сколько решений имеет система уравнений 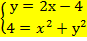 ? Решить графически.
? Решить графически.
8.Укажите систему уравнений, которая не имеет решений
а) 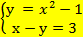 б)
б) 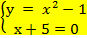 в)
в) 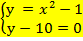 г) Все три системы
г) Все три системы
9.Решить систему: 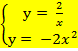
10. Решить неравенство  > -2х2 (по предыдущему чертежу)
> -2х2 (по предыдущему чертежу)
На каком промежутке график функции у=  лежит выше графика функции у= -2х2?
лежит выше графика функции у= -2х2?
11.Найти область определения функции у= 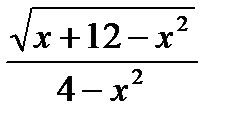
12.По формуле функции назовите ее график
1)у=  2)у=х3+2 3)у=2
2)у=х3+2 3)у=2 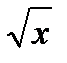 4)у= -8 5)х=2 6)у= -
4)у= -8 5)х=2 6)у= - 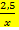 -1
-1
13. Задайте функцию графически:
у=х2+5; у=х2-3; у = (х-3)2 ; у = (х+2)2; у = (х+3)2-4
14.Найти наибольшее и наименьшее значения функции: а) у = 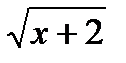 б) у= -х2+8х-12
б) у= -х2+8х-12
15. Постройте и прочитайте график функции у = 
Вопросы для самопроверки:
1. Способы задания функции.
2. Какие функции называются периодическими?
3. Как расположены графики взаимно-обратных функций.
4. Какие функции называются возрастающими?
5. Какие функции называются убывающими?
6. Какие функции называются монотонными?
7. Что такое функция?
8. Что такое область определения функции?
9. Что такое множество значений функции?
10. Какие функции называются чётными?
11. Какие функции называются нечётными?
12. Свойства графиков чётной и нечётной функций.
13. Какие функции называются обратными?
14. Назовите пары взаимно обратных функций.
15. Какие свойства различны у взаимно обратных функций?
16. Какие свойства одинаковы у взаимно обратных функций?
17. Назовите область определения: 1) обратной пропорциональности 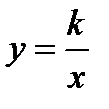 2) функции у=
2) функции у= 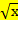
18. Что является графиком функции:
а)линейной у = кх+в б) прямой пропорциональности у=кх
в) квадратичной функции у = ах2+вх+с г) обратной пропорциональности у= 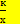
д) степенной функции у=х3 е) степенной у = 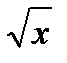
ж) модуль х
Форма контроля: проверка конспекта и устный опрос.
Самостоятельная работа № 12
Показательная функция
y = ax
| y |
| x |
| a>1 |
| a<1 |
| y |
| x |
| y=2x |
| y=0,5x |
| y=3x |
Степенная функция
y = xn
| y |
| x |
| y=x2 |
| y=x4 |
| y |
| x |
| y=x3 |
| y=x5 |
Решить самостоятельно.
Задание. Построить графики функций: y = 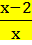 ; y =
; y = 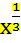 ; y =
; y = 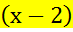 -1
-1
Форма контроля: проверка конспекта и устный опрос.
Самостоятельная работа № 13
Логарифмическая функция
Функция y= 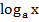 , (х
, (х 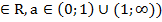 ) называется логарифмической функцией.
) называется логарифмической функцией.
Логарифмическая функция y= 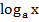 является обратной по отношению к показательной функции у=
является обратной по отношению к показательной функции у= 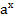 (х
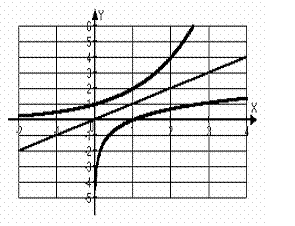
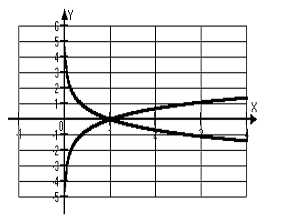
(х 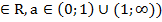 ) . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
) . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
| y |
| x |
| y=log2 x |
| y=log0,4 x |
| y=log4 x |
| y |
| x |
| a>1 |
| a<1 |
Приведем основные свойства логарифмической функции:
1) Область определения: D(y) =R+ .
2) Область значений функции: E(y) =R.
3) Логарифм единицы равен нулю, логарифм основания равен единице: 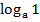 =0,
=0, 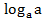 =0, .
=0, .
4) Функция y= 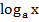 ,
, 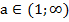 возрастает в промежутке
возрастает в промежутке 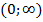 (рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
(рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
5) Функцияy= 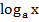 , (х
, (х 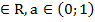 , убывают в промежутке
, убывают в промежутке 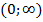 . При этом, логарифмы чисел, меньших единицы, положительны, а - больших единицы, отрицательны.
. При этом, логарифмы чисел, меньших единицы, положительны, а - больших единицы, отрицательны.
4. Найти область определения функции: y= 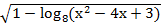
Решение. Поскольку логарифмическая функция определена только для положительных чисел, а квадратный корень – для неотрицательных чисел, задача сводится к решению системы неравенств:
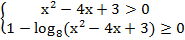
Левую часть первого неравенства разложим на множители, а во втором заменим 1 на 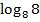 :
:
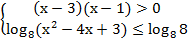
Так как основание логарифма8 >1 , то, согласно свойствам логарифма, переходим к системе: 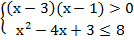 т.е.
т.е. 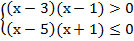
Последняя система равносильна неравенству: 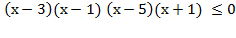 ,
,
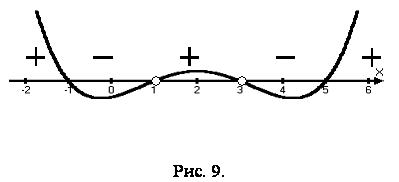
которое решается методом интервалов (причем x≠3, и x ≠ 1 ). С помощью рис. 9 получаем ответ:[-1;1) 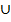 (3;5].
(3;5].
Контрольные вопросы.
1. Дайте определение логарифмической функции.
2. Какие область определения и область значения функции у = logax?
3. В каком случае функция у = logax является возрастающей, в каком убывающей?
4. При каких значениях x функции у = logax принимает положительные значения, при каких отрицательные?
Тест для самопроверки. ( Варианты ответов: да нет)
1. Логарифмическая функция у = logax определена при любом х
2. Функция у = logax определена при а > 0, а =/= 1, х > 0.
3. Областью определения логарифмической функции является множество действительных чисел.
4. Областью значений логарифмической функции является множество действительных чисел.
5. Логарифмическая функция – четная.
6. Логарифмическая функция – нечетная.
7. Функция у = logax – возрастающая при а >1.
8. Функция у = logax при положительном, но меньшем единицы основании, – возрастающая.
9. Логарифмическая функция имеет экстремум в точке (1; 0).
10. График функции у = logax пересекается с осью ОХ.
11. График логарифмической функции находится в верхней полуплоскости.
12. График логарифмической функции симметричен относительно ОХ.
13. График логарифмической функции пересекает ОХ в точке (1; 0).
14. График логарифмической функции находится в 1 и 4 четвертях.
15. Существует логарифм отрицательного числа.
16. Существует логарифм дробного положительного числа.
17. График логарифмической функции проходит через точку (0; 0).
Самостоятельная работа №14
Тест для самопроверки.
18. Тригонометрические функции определены при любом х
19. Функция у = ctg x определена на (π n; π+ π n),.
20. Областью определения функции у =tg x является объединение интервалов (- 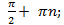
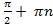 .)
.)
21. Областью значений каких тригонометрических функций является множество [-1; 1]
22. При построении тригонометрических функций мы используем ….меру измерения углов.
23. Функцияy = sin x представляется графиком…….
24. Областью определения каких тригонометрических функций является R
25. Какие тригонометрические функции четные, нечетные.
26. Тригонометрические функции периодичны.
27. sin x > 0 при x 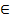 (2 π n; n + 2 π n), n
(2 π n; n + 2 π n), n 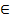 Z
Z
28. cos x < 0 при x 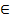 (
(  + 2 π n;
+ 2 π n; 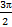 + 2 π n), n
+ 2 π n), n 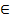 Z
Z
29. Нули функцииy =cos x : 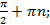 n
n 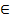 Z
Z
30. Экстремумы какой функции xmin = π + 2 π n, n 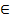 Z; ymin = -1 xmax = 2 π n, n
Z; ymin = -1 xmax = 2 π n, n 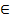 Z; ymin = 1?
Z; ymin = 1?
31. Как можно получить друг из друга графики функций y = sinx и y = cosx ?
32. Логарифмическая функция имеет экстремум в точке (1; 0).
33. График функции у= cos x пересекается с осью ОХ в точках….
34. График логарифмической функции находится в верхней полуплоскости.
35. График логарифмической функции симметричен относительно ОХ.
36. График логарифмической функции пересекает ОХ в точке (1; 0).
37. График логарифмической функции находится в 1 и 4 четвертях.
38. Существует логарифм отрицательного числа.
39. Существует логарифм дробного положительного числа.
40. График логарифмической функции проходит через точку (0; 0).
Самостоятельная работа №15(2 часа)
Цель: изучить преобразования графиков функций.
изучить симметрию графиков относительно прямой Y=X.
| Способы построения графиков функций | |
| «по точкам» | |
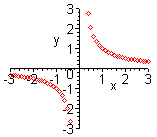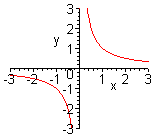 | Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями. (На графике функция 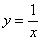 ). ). |
| Путем сдвига графиков основных функций | |
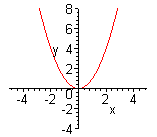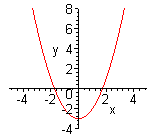 | Чтобы построить график функции 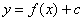 , можно или график функции , можно или график функции 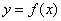 сдвинуть вдоль оси сдвинуть вдоль оси 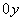 на на 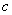 единиц в сторону, совпадающую со знаком единиц в сторону, совпадающую со знаком 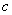 , или перенести параллельно ось , или перенести параллельно ось 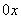 в сторону, противоположную знаку в сторону, противоположную знаку 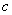 . (На примере функции . (На примере функции 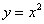 и и 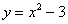 ). ). |
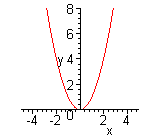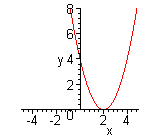 | Чтобы построить график функции 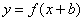 , можно или график функции , можно или график функции 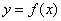 вдоль оси вдоль оси 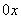 на на 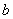 единиц в сторону, противоположную знаку единиц в сторону, противоположную знаку 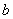 , или перенести параллельно ось , или перенести параллельно ось 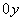 в сторону, совпадающую со знаком в сторону, совпадающую со знаком 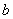 . (На примере функции . (На примере функции 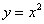 и и 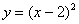 ). ). |
| путем симметричного отображения относительно осей координат | |
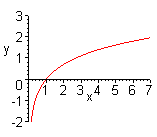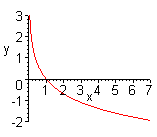 | Чтобы построить график функции 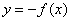 , можно построить изображение, симметричное графику функции , можно построить изображение, симметричное графику функции 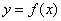 относительно оси относительно оси 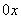 . (На примере функции . (На примере функции 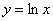 и и 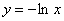 ). ). |
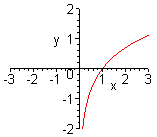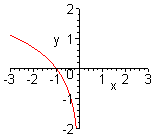 | Чтобы построить график функции 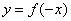 , можно построить изображение, симметричное графику функции , можно построить изображение, симметричное графику функции 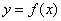 относительно оси относительно оси 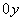 . (На примере функции . (На примере функции 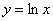 и и 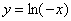 ). ). |
| Путем деформирования графиков основных функций | |
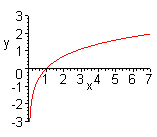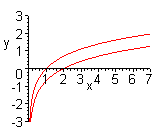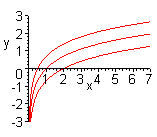 | Чтобы построить график функции 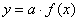 при при 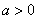 , можно график функции , можно график функции 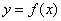 растянуть (сжать) вдоль оси растянуть (сжать) вдоль оси 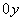 , если , если 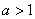 ( ( 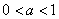 ). (На примере функции ). (На примере функции 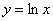 , , 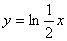 и и 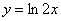 ). ). |
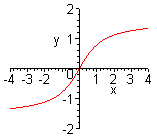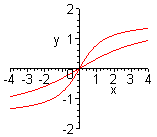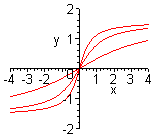 | Чтобы построить график функции 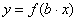 при при 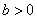 , можно график функции , можно график функции 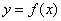 растянуть (сжать) вдоль оси растянуть (сжать) вдоль оси 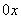 , если , если 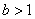 ( ( 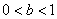 ). ). 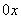 . . 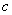 .(На примере функции .(На примере функции 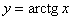 , , 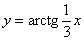 и и 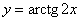 ). ). |
| Способы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины | |
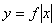 | |
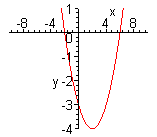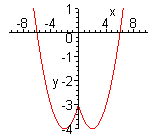 | Функция 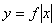 четная. Чтобы построить ее график, достаточно построить для четная. Чтобы построить ее график, достаточно построить для 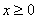 график функции график функции 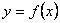 , а затем достроить его левую часть, симметричную правой относительно оси , а затем достроить его левую часть, симметричную правой относительно оси 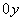 . (На примере функции . (На примере функции 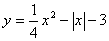 ). ). |
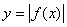 | |
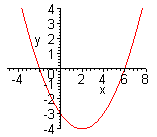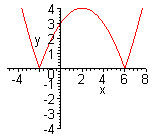 | Можно данную функцию рассматривать как совокупность двух функций: 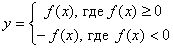 . Чтобы построить график функции . Чтобы построить график функции 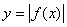 , достаточно построить график функции , достаточно построить график функции 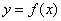 и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси 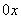 . (На примере функции . (На примере функции 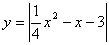 ) ) |
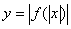 | |
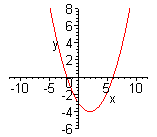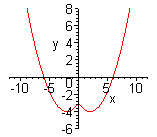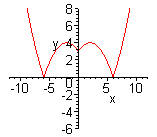 | Функция 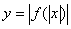 четная. Построить для четная. Построить для 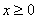 график функции график функции 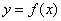 , затем его симметрично отразить относительно оси , затем его симметрично отразить относительно оси 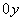 , и, наконец, ту часть полученного графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси , и, наконец, ту часть полученного графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси 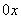 . (На примере функции . (На примере функции 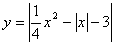 ). ). |
| Кусочно-линейная функция | |
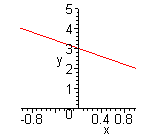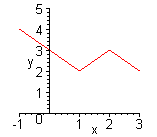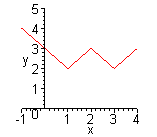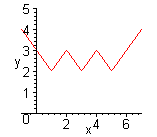 | Графиком кусочно-линейной функции является ломаная линия. Для построения графика находят уравнения звеньев ломаной.(Функция 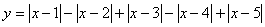 ). Уравнения звеньев ломаной: ). Уравнения звеньев ломаной: 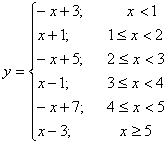 |
Преобразования графиков с помощью параллельного переноса
| х |
| у |
| у = –(х – 4)2 |
| –4 |
| х |
| у |
| –3 |
| у = (х – 3)2 |
| х |
| у |
| у = (х + 2)2 – 4 |
| +2 |
| –4 |
| х |
| у |
| +2 |
| у = х2 + 2 |
| Вариант 1 | Номер задания | |||||||||||||||||||||||||||||||||||||||
| Вариант ответа | ||||||||||||||||||||||||||||||||||||||||
| Укажите для каждой функции ее график 1. у = –х2 + 3 3. у = (х – 3)2 5. у = (х – 4)2 – 2 2. у = –х2 + 4 4. у = –(х + 3)2 6. у = (х + 4)2 – 2 | ||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||
Найти область определения функции.
1. 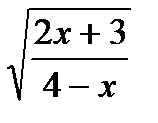 ;
;
2. 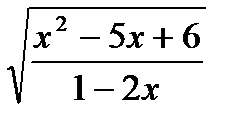
3. 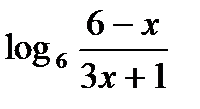 ;
;
4. 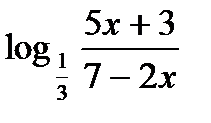
№5.19 (построить графики)
1) 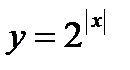 ;
;
2) 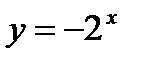 ;
;
3) 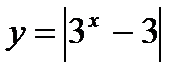 ;
;
4) 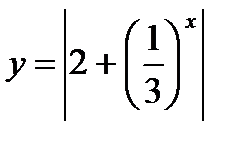 ;
;
5) 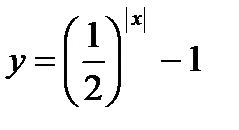 ;
;
6) 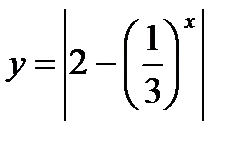 ;
;
7) 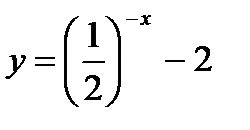 .
.
№ 5.20 (Решить уравнения графически):
1) 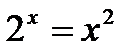
2) 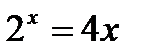
3) 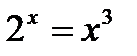
4) 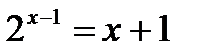
5) 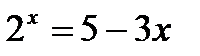
6) 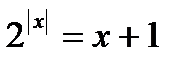
Контрольные вопросы.
Какие преобразования вы знаете?
Какие преобразования позволяют сдвигать график функции вдоль осей?
Какие преобразования позволяют сжимать график функции вдоль осей?
Какие преобразования позволяют симметрично отображать график функции относительно осей?
Самостоятельная работа №11
Тема 4.1. Функции и их свойства
Самостоятельная работа (4 часа)
Цель: Выработать навык построения графиков элементарных функций, изучить взаимное расположение графиков обратных функций.
Линейная функция
y = kx + b, k – угловой коэффициент, b – свободный член
| y |
| x |
| xA |
| xB |
