Положение тела в пространстве. Системы отсчета.
Класс
Рабочая тетрадь № 1
для учащихся общеобразовательных учреждений
Москва
Издательский центр «Вентана-Граф»
ББК 22.3я721
Ф48
Авторы: А.В. Грачёв, В.А. Погожев, П.Ю. Боков
Ф 48Физика: 10 класс : рабочая тетрадь № 1 для учащихся общеобразовательных учреждений / А.В. Грачёв, В.А. Погожев, П.Ю. Боков. — М. : «Вентана-Граф», 2011. — 108 с. : ил.
ISBN
Рабочие тетради вместе с учебником, тетрадью для лабораторных работ, методическим пособием для учителя составляют учебно-методический комплект по физике для 10 класса общеобразовательных учреждений. В тетради № 1 представлены задания по темам «Кинематика» и «Динамика».
Соответствует федеральному компоненту государственных образовательных стандартов основного общего образования (2004 г.).
ББК 22.3я721
© Издательский центр «Вентана-Граф», 2011
ISBN
Предисловие
Дорогие старшеклассники!
В рабочей тетради к каждому параграфу учебника приведены задания, которые вы будете выполнять самостоятельно во время урока или дома. Перед выполнением задания в классе внимательно выслушайте рассказ или объяснения учителя, а при работе с тетрадью дома прочитайте текст параграфа из учебника, разберите примеры решения подобных задач.
Задания рабочей тетради составлены с пропусками, которые следует заполнить. Это могут быть отдельные слова или выражения, формулы, вычисления, данные в таблицах, графики, которые нужно построить при выполнении задания. Аккуратно заполняйте эти пропуски карандашом, чтобы иметь возможность исправить (стереть ластиком) допущенные ошибки. При вычерчивании графиков, схем или осей координат используйте чертёжные инструменты (линейку, треугольник и др.). В некоторых заданиях рабочей тетради приведены несколько вариантов ответа, из которых нужно выбрать правильный и отметить его так, как указано в задании (подчеркнуть, поставить значок или цифру). Прежде чем это сделать, внимательно прочтите и обдумайте все предложенные варианты ответа.
Задания к параграфам учебника следуют в порядке от простых к более сложным. Самые сложные задания отмечены знаком *.
Так же как в учебнике, некоторые параграфы рабочей тетради отмечены знаком  , их материал предназначен для тех, кто изучает физику на профильном уровне. Эти задания, наряду со сложными (*), будут полезны также тем, кто собирается сдавать единый государственный экзамен по физике.
, их материал предназначен для тех, кто изучает физику на профильном уровне. Эти задания, наряду со сложными (*), будут полезны также тем, кто собирается сдавать единый государственный экзамен по физике.
Желаем вам успехов.
Авторы
Глава 1. Кинематика
1. Отметьте знаком Ú (галочкой)правильный ответ:
Кинематика – раздел механики, в котором рассматривают:
движение тел □
причины изменения характера движения тел □
способы описания механическое движение тел без выяснения причин
его возникновения или изменения □
2. Отметьте знаком Ú(галочкой) полный правильный ответ:
Механическим движением называют:
изменение положения тела с течением времени □
изменение положения тела или его частей в пространстве относительно других тел с течением времени □
изменение положения тела или его частей относительно других тел □
3. Зачеркните в таблице (справа) неверные утверждения.
| Реальное тело при описании его движения можно заменить точечным, | если оно имеет правильную форму; если масса тела достаточно мала; если можно пренебречь различием в движении отдельных частей тела |
| Точечное тело – это | объект, размерами которого можно пренебречь по сравнению с характерными масштабами решаемой задачи; объект, имеющий малую массу; объект правильной формы. |
4. Отметьте знаком Ú (галочкой)случаи, когда искусственный спутник Земли может быть принят за точечное тело:
при описании его движение по орбите □
при корректировке его ориентации □
при выводе его на орбиту □
при расчёте силы, действующей на него в плотных слоях атмосферы □
Положение тела в пространстве. Системы отсчета.
Упражнения
5. Закон движения точечного тела вдоль оси Х имеет вид: х(t) = 1 + 4t – 2t  . Все величины в законе движения измерены в СИ. Заполните таблицу, а затем постройте график движения этого тела на рис. 1.
. Все величины в законе движения измерены в СИ. Заполните таблицу, а затем постройте график движения этого тела на рис. 1.
| t, с | |||||
| x(t), м |
Рис. 1
6. Законы движения точек 1 и 2, движущихся вдоль оси Х, имеют вид: х1(t) = 5 – 2t и х2(t) = 1 + 2t, где х измеряют в метрах, а t — в секундах.
Выполните следующие задания: а) определите координаты точек в моменты времени t = 0; 1; 2; 3 с; б) постройте графики движения точек на рис.2; в) определите координату и время встречи точек 1 и 2.

Рис. 2
7. Координаты движущегося по плоскости XY точечного тела изменяются по закону: x(t) = 5 – 3t; y(t) = 1 + t, где х и y измеряют в метрах, а t — в секундах.
Выполните следующие задания: а) определите координаты точки в моменты времени t = 0; 1; 2; 3 с; б) постройте графики движения точки x(t) и y(t); в) получите уравнение траектории тела y(x) и постройте траекторию тела на плоскости XY .
Перемещение. Путь
1. Дополните предложения, вставляя пропущенные слова.
Перемещением точечного тела называют ____________, начало которого совпадает с ______________________, а конец — с ______________________
тела.
Проекция вектора перемещения на координатную ось равна разности __________________________________________________________________
Проекция вектора перемещения на координатную ось будет положительной, если направление от проекции начала вектора перемещения к проекции его конца __________________ с направлением ____________________
____________________
Проекция вектора перемещения на координатную ось будет отрицательной, если направление от проекции начала вектора перемещения к проекции его конца _____________________________________ этой координатной оси.
Если вектор перпендикулярен координатной оси, то его проекция на данную ось равна __________________.
Если перемещения проекций точки на оси X и Y равны _________ и __________, то перемещение 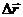 этого тела равно ________________.
этого тела равно ________________.
Модуль перемещения точечного тела и перемещения его проекций вдоль осей X и Y удовлетворяют соотношению:
_________________________________________________
Проекция суммы перемещений на координатную ось равна сумме ______________________________________________________.
2. На рис. 3 изображены векторы последовательных перемещений точечного тела Δ 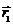 , …, Δ
, …, Δ  . Заполните таблицу, определив по рис. 3 указанные величины.
. Заполните таблицу, определив по рис. 3 указанные величины.

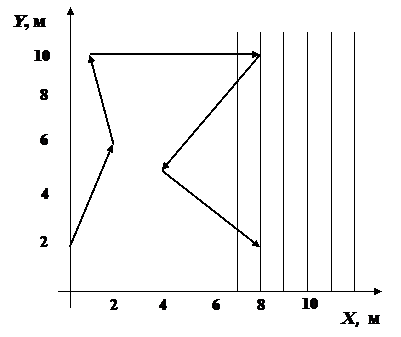
Рис. 3.
| Вектор перемещения | Проекция вектора перемещения на ось X, м | Проекция вектора перемещения на ось Y, м | Модуль вектора перемещения, м |
Δ 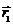 | |||
Δ 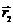 | |||
Δ  | |||
Δ  | |||
Δ  | |||
Вектор результирующего перемещения Δ  |
3. Отметьте знаком Ú (галочкой) правильные утверждения:
путь – это все расстояние, пройденное телом за рассматриваемый промежуток времени □
путь – это модуль перемещения тела за рассматриваемый промежуток времени □
путь – это сумма проекций перемещений тела на координатные оси □
путь равен длине траектории тела при его движении в одном направлении □
путь равен сумме длин участков траектории, пройденных телом в одном направлении □
путь равен модулю перемещения тела за рассматриваемый промежуток времени при прямолинейном движении в одном направлении □
путь больше модуля перемещения тела за рассматриваемый промежуток времени при криволинейном движении □
4. Определите общий путь, пройденный телом из упражнения 2. Сравните полученный результат с модулем результирующего перемещения.
Решение.
Ответ:
5. Законы движения точечного тела вдоль осей координат X и Y в СИ имеют вид: х(t) = 2 + 5t, y(t) = 10 – t в течение двух первых секунд движения, х(t) = 6 + 3t, y(t) = 6t – 4, в последующие две секунды. Постройте график зависимости y(х) на рис. 4. На этом графике отметьте положения тела в моменты времени 0; 1; 2; 3 и 4 с. Синим карандашом изобразите перемещение тела за 3 с от начала движения, зелёным — с первой по третью, чёрным — с первой по четвёртую, красным — со второй по четвёртую секунды движения. Определите модули этих перемещений, их проекции на координатные оси и пути, пройденные за соответствующие интервалы времени. Полученные ответы внесите в таблицу.

Рис. 4.
| Интервал времени, с | 0 – 3 | 1 – 3 | 1 – 4 | 2 – 4 |
| ∆r |  | |||
| ∆x | ||||
| ∆y | ||||
| S |
Какие из полученных значений модулей перемещений и путей совпадают? Почему?
Ответ:
Скорость
1. Установите соответствие между следующими физическими величинами и их определениями:
1) средняя путевая скорость υ  ; 2) средняя скорость
; 2) средняя скорость 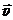 ср.; 3) скорость (мгновенная скорость)
ср.; 3) скорость (мгновенная скорость) 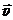 в момент времени t.
в момент времени t.
А) отношение пути S, пройденного телом за рассматриваемый промежуток времени  , к длительности этого промежутка;
, к длительности этого промежутка;
Б) отношение перемещения  тела за достаточно малый промежуток времени
тела за достаточно малый промежуток времени  , начинающийся сразу после момента времени t, к длительности этого промежутка;
, начинающийся сразу после момента времени t, к длительности этого промежутка;
В) отношение перемещения  , совершенного телом за рассматриваемый промежуток времени
, совершенного телом за рассматриваемый промежуток времени  , к длительности этого промежутка.
, к длительности этого промежутка.
Ответ (А, Б, В) укажите в таблице.
υ  | 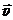 ср. ср. | 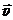 |
2. Отметьте знаком Ú (галочкой) правильные утверждения:
а) Модуль средней скорости равен средней путевой скорости:
при прямолинейном движении в одном направлении; □
при криволинейном движении в одном направлении; □
при любом прямолинейном движении. □
б) Направление вектора средней скорости совпадает с направлением вектора перемещения:
только при прямолинейном движении; □
только при прямолинейном движении в одном направлении; □
только при криволинейном движении; □
при любом движении. □
3. В приведённом списке подчеркните скалярные величины одной чертой, а векторные — двумя чертами.
Путь, перемещение, проекция перемещения на координатную ось, мгновенная скорость, средняя скорость, средняя путевая скорость, проекция скорости на координатную ось.
4. На рис. 5 изображены векторы скорости восьми точечных тел. Определите, используя линейку, проекции этих скоростей на координатные оси и модули этих скоростей. Результаты занесите в таблицу.
| № | ||||||||
| υ | ||||||||
| υx | ||||||||
| υy |
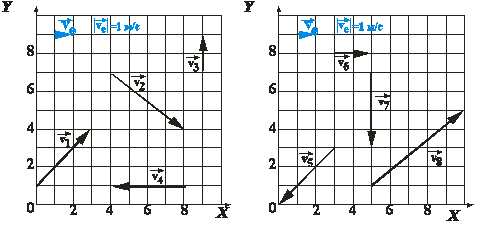
Рис. 5.
5. На рис. 6 приведён график модуля скорости точечного тела от времени. Определите пути, пройденные телом за промежутки времени, указанные в таблице. Результаты занесите в таблицу.

Рис. 6
| Промежутки времени, с | 0–3 | 3–5 | 5–10 | 0–10 | 2–8 |
| Путь, м |
6. Лодка проплыла первую половину пути с постоянной скоростью, модуль которой υ 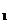 = 0,5 м/с, а вторую половину пути — с υ
= 0,5 м/с, а вторую половину пути — с υ 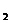 = 2 м/с. Определите среднюю путевую скорость лодки.
= 2 м/с. Определите среднюю путевую скорость лодки.
Решение.
Время прохождения первой половины пути t1 = __________ = ______c,
время прохождения второй половины пути t2 = ___________ = _____c,
полное время движения t = _____________________ = _______c.
Искомая путевая скорость υ  = ______________ = __________ м/с
= ______________ = __________ м/с
Ответ: υ  = ____________ м/с.
= ____________ м/с.
7. Поезд шёл половину времени движения со скоростью, модуль которой υ 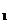 = 60 км/ч, а другую половину — с υ
= 60 км/ч, а другую половину — с υ 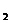 = 80 км/ч. Определите среднюю путевую скорость поезда.
= 80 км/ч. Определите среднюю путевую скорость поезда.
Решение.
Ответ: υ  = ____________ м/с.
= ____________ м/с.
8. На рис. 7 приведены графики движения трёх точечных тел вдоль оси Х. Определите проекции средних скоростей этих тел на ось Х и средние путевые скорости за первую (с 0 по 4 секунды) и вторую (с 4 по 8 секунды) части времени движения тел, а также указанные величины за все время движения.
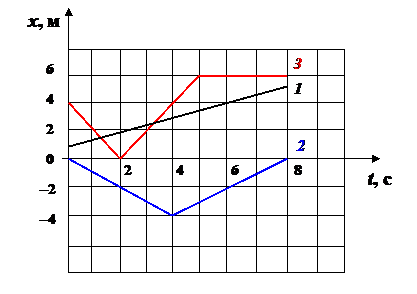
Рис. 7.
| № | Величины | ||||||||||
 |  | υx |  |  | 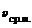 | ||||||
| 1 | |||||||||||
| 2 | |||||||||||
| 3 | |||||||||||
9. Пункты A, B и C расположены в вершинах правильного треугольника. Вертолёт взлетает в пункте А, последовательно облетает пункты B и C и возвращается в А. Между каждыми двумя пунктами он движется прямолинейно. На участке AB модуль его скорости равен υ1, на участках BC и CA — υ2 и υ3 соответственно. Определите среднюю путевую скорость и модуль средней скорости вертолёта на всём пути АВСА.
Решение.
Ответ:
Рис. 8
Ответ: х10 = ______ х20 = _______ v1х = ________ v2х = ________
Закон движения тела 1 х1(t) = __________________
закон движения тела 2 x2(t) = __________________
5. Точечное тело движется по плоскости XY. На рис. 9 показаны графики зависимости его координат х и y от времени t. Запишите закон движения этого тела в проекциях на координатные оси. Определите модуль скорости этого тела. Постройте траекторию движения тела за первые 5 с.



Рис. 9
Ответ: закон движения тела: х(t) = ___________ y(t) = _____________
Модуль скорости тела v = _______ м/с.
Графический способ решения
Задача 1. Из пунктов А и В, находящихся на расстоянии 300 км, одновременно выезжают навстречу друг другу два автомобиля со скоростями, модули которых υ 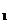 = 50 км/ч и υ
= 50 км/ч и υ 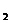 = 100 км/ч. Определите графическим способом время tв встречи автомобилей и расстояние l от пункта А до места встречи.
= 100 км/ч. Определите графическим способом время tв встречи автомобилей и расстояние l от пункта А до места встречи.
Решение.
Шаг 0. Выбор модели.
Будем пренебрегать размерами _____________ и считать, что пункты А и В расположены на одной прямой.
Шаг 0. Выбор модели.
Будем считать поезда ________________________________.
Шаг 7. Решение системы.
Подставив (1) и (2) для момента времени t = tвв (3), получим: _________________________________________________________________
Отсюда: tв = __________, S = _____________
Шаг 8. Анализ полученного результата и расчёт ответа.
Проверкаразмерности полученных результатов.
[tв] = _____________ и [S] = _______________.
Таким образом, сточки зрения размерности полученный результат _______________________________________.
Исследуем, как будут изменяться полученные значения S и tв при изменениях величин, входящих в полученные зависимости.
Если разность модулей скоростей поездов υ 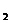 – υ
– υ 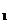 стремится к нулю, то _____________. Если увеличивать скорость «Спутника» υ
стремится к нулю, то _____________. Если увеличивать скорость «Спутника» υ 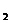 при неизменном υ
при неизменном υ 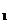 , то ___________________. Если уменьшать скорость электрички υ
, то ___________________. Если уменьшать скорость электрички υ 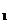 при неизменном υ
при неизменном υ 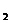 , то ____________________.
, то ____________________.
Полученные выводы _____________ здравому смыслу и жизненному опыту, т. е. полученные ответы __________ физический смысл.
Проводим численный расчёт, подставив в полученное выражение числовые данные: ________________, ________________
Ответ: Поезда встретятся через tв = _____ ч на расстоянии S = ______ км от станции.
Задача 3. Пешеход и велосипедист движутся навстречу друг другу со скоростями, модули которых равны 2 м/с и 10 м/с соответственно. Расстояние между ними в начальный момент времени равно 240 м. Найдите графическим и аналитическим способами место и время встречи пешехода и велосипедиста.
Решение.
 Задача 4. Колонна длиною L, состоящая из физкультурников, которые следуют друг за другом на равных расстояниях, движется с постоянной по модулю скоростью U. Навстречу им бежит тренер со скоростью, модуль которой равен V (V > U). Каждый спортсмен, с которым поравнялся тренер, мгновенно разворачивается и продолжает движение с прежней по модулю скоростью. Определите длину перестроившейся колонны во главе с тренером.
Задача 4. Колонна длиною L, состоящая из физкультурников, которые следуют друг за другом на равных расстояниях, движется с постоянной по модулю скоростью U. Навстречу им бежит тренер со скоростью, модуль которой равен V (V > U). Каждый спортсмен, с которым поравнялся тренер, мгновенно разворачивается и продолжает движение с прежней по модулю скоростью. Определите длину перестроившейся колонны во главе с тренером.
Сложение движений
1. Отметить знаком Ú (галочкой)правильные утверждения:
От выбора системы отсчёта зависят:
только координаты тел; □
только зависимости координат тел от времени; □
только перемещения тел и скорости их движения; □
все перечисленные физические величины. □
2. Дополните предложения, вставляя пропущенные слова.
Если система отсчёта X′Y′ движется поступательно относительно системы отсчёта XY, то
а) перемещение 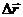 точечного тела в системе отсчёта XY равно сумме ____________________ этого тела в системе отсчёта X′Y′ и _____________________ начала системы отсчёта X′Y′ относительно системы отсчёта XY:____________________________;
точечного тела в системе отсчёта XY равно сумме ____________________ этого тела в системе отсчёта X′Y′ и _____________________ начала системы отсчёта X′Y′ относительно системы отсчёта XY:____________________________;
б) скорость 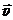 точечного тела в системе отсчёта XY равна сумме ___________________ этого тела в системе отсчёта X′Y′ и _________________________, с которой начало отсчёта системы отсчёта X′Y′ движется относительно системы отсчёта XY:
точечного тела в системе отсчёта XY равна сумме ___________________ этого тела в системе отсчёта X′Y′ и _________________________, с которой начало отсчёта системы отсчёта X′Y′ движется относительно системы отсчёта XY:
3. Поезд движется относительно платформы со скоростью, модуль которой равен 30 км/ч. По ходу его движения с конца поезда идёт пассажир со скоростью, модуль которой относительно пола вагона равен 1,5 км/ч. Из начала поезда навстречу ему идёт проводник. Модуль его скорости относительно вагона равен 3 км/ч.
а) Определите расстояние, на которое перемещается относительно платформы пассажир:
за 5 мин ______________; за 10 мин _________________;
б) Определите расстояние, на которое перемещается относительно платформы проводник:
за 5 мин ______________; за 10 мин _________________;
в) Определите модули скоростей:
пассажира относительно платформы ________________________км/ч;
проводника относительно платформы _______________________км/ч;
пассажира относительно проводника _______________________км/ч;
проводника относительно пассажира _______________________км/ч.
г) Как изменяется расстояние между пассажиром и проводником:
за 5 мин ___________________; за 10 мин ____________________.
 4. Авианосец движется относительно берега моря на запад со скоростью
4. Авианосец движется относительно берега моря на запад со скоростью 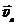 , модуль которой равен 10 м/с. С берегом связана система отсчёта XYZ, ось X которой направлена на запад, ось Y — на юг, а ось Z — вверх. Система отсчёта X′Y′Z′, оси которой параллельны соответствующим осям системы отсчёта XYZ, связана с авианосцем. С авианосца взлетает самолёт, перемещаясь относительно его палубы со скоростью, проекция которой на ось
, модуль которой равен 10 м/с. С берегом связана система отсчёта XYZ, ось X которой направлена на запад, ось Y — на юг, а ось Z — вверх. Система отсчёта X′Y′Z′, оси которой параллельны соответствующим осям системы отсчёта XYZ, связана с авианосцем. С авианосца взлетает самолёт, перемещаясь относительно его палубы со скоростью, проекция которой на ось 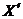 равна 100 м/с, а на ось
равна 100 м/с, а на ось 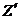 равна 5 м/с. Одновременно по палубе бежит офицер со скоростью, проекция которой на ось
равна 5 м/с. Одновременно по палубе бежит офицер со скоростью, проекция которой на ось 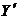 равна 2 м/с. Определите величины, указанные в левом столбце, и заполните таблицу.
равна 2 м/с. Определите величины, указанные в левом столбце, и заполните таблицу.
| Величины | Авианосец | Самолёт | Офицер | |
| Перемещение за 1 с: | вдоль оси X′ | |||
| вдоль оси Y′ | ||||
| вдоль оси Z′ | ||||
| вдоль оси X | ||||
| вдоль оси Y | ||||
| вдоль оси Z | ||||
Проекция скорости в системе отсчёта 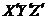 : : | на ось X′ | |||
| на ось Y′ | ||||
| на ось Z′ | ||||
Проекция скорости в системе отсчёта 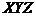 : : | на ось X | |||
| на ось Y | ||||
| на ось Z |
 5. Модуль скорости течения реки шириной L = 4 м равен 2 м/с. Направление скорости течения реки совпадает с положительным направлением оси X, связанной с берегом. Ось Y направлена горизонтально и перпендикулярно оси X. Собака переплывает реку так, что проекция её скорости относительно воды на ось Y равна 1 м/с, а на ось X отрицательна и равна –0,5 м/с. Сделайте рисунок и изобразите:
5. Модуль скорости течения реки шириной L = 4 м равен 2 м/с. Направление скорости течения реки совпадает с положительным направлением оси X, связанной с берегом. Ось Y направлена горизонтально и перпендикулярно оси X. Собака переплывает реку так, что проекция её скорости относительно воды на ось Y равна 1 м/с, а на ось X отрицательна и равна –0,5 м/с. Сделайте рисунок и изобразите:
1) перемещение за первую секунду: собаки относительно воды 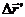 — синим карандашом; воды относительно берега
— синим карандашом; воды относительно берега 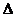
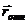 — зелёным карандашом;
— зелёным карандашом;
собаки относительно берега 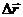 — красным карандашом.
— красным карандашом.
2) указанные перемещения за последующие секунды переправы.
Определите по рисунку: а) время переправы; б) смещение Dx собаки вдоль берега за время переправы.
Ответ: время переправы Dt = ______ с; снос ∆х = ________ м.
 6. Известно, что при движении велосипедиста и бегуна в одном направлении бегун отстаёт от велосипедиста на S
6. Известно, что при движении велосипедиста и бегуна в одном направлении бегун отстаёт от велосипедиста на S 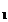 = 120 м за каждую минуту, а если они движутся навстречу друг другу, не меняя модулей скорости, то расстояние между ними уменьшается на S
= 120 м за каждую минуту, а если они движутся навстречу друг другу, не меняя модулей скорости, то расстояние между ними уменьшается на S 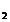 = 600 м за каждые две минуты. Определите модули скорости велосипедиста и пешехода.
= 600 м за каждые две минуты. Определите модули скорости велосипедиста и пешехода.
Решение.
Ответ: модуль скорости велосипедиста v1 = ________ м/с;
модуль скорости бегуна v2 = __________ м/с.
 7. Сколько времени займёт рейс лодки по прямой от пристани А до пристани В (на другом берегу вниз по течению) и обратно, если модуль скорости течения постоянен и всюду равен
7. Сколько времени займёт рейс лодки по прямой от пристани А до пристани В (на другом берегу вниз по течению) и обратно, если модуль скорости течения постоянен и всюду равен  ? Модуль скорости лодки относительно воды равен v; расстояние вдоль берега от пристани А до точки, расположенной напротив пристани В, равно
? Модуль скорости лодки относительно воды равен v; расстояние вдоль берега от пристани А до точки, расположенной напротив пристани В, равно 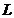 ; ширина реки —
; ширина реки — 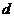 .
.
 8. На противоположных берегах прямолинейного участка реки находятся две пристани А и В, расстояние между которыми S = 130 м, а прямая АВ составляет угол a = 60° с берегом. Модуль скорости воды по всей ширине реки одинаков и равен u = 0,1 м/с. С пристаней одновременно отплыли два катера и, двигаясь все время по прямой АВ с постоянными относительно воды скоростями, модули которых равны, встретились через t = 36 с. Определите модуль v скорости катеров относительно воды.
8. На противоположных берегах прямолинейного участка реки находятся две пристани А и В, расстояние между которыми S = 130 м, а прямая АВ составляет угол a = 60° с берегом. Модуль скорости воды по всей ширине реки одинаков и равен u = 0,1 м/с. С пристаней одновременно отплыли два катера и, двигаясь все время по прямой АВ с постоянными относительно воды скоростями, модули которых равны, встретились через t = 36 с. Определите модуль v скорости катеров относительно воды.
 9. В вершинах равностороннего треугольника с длиной стороны L находятся три черепахи, размеры которых много меньше L. Первая черепаха смотрит на вторую, вторая — на третью, а третья — на первую. В некоторый момент черепахи начинают двигаться с одинаковыми по модулю скоростями. При этом каждая черепаха в любой момент времени движется в направлении той черепахи, на которую она смотрит. Определите время движения черепах до их встречи в центре квадрата.
9. В вершинах равностороннего треугольника с длиной стороны L находятся три черепахи, размеры которых много меньше L. Первая черепаха смотрит на вторую, вторая — на третью, а третья — на первую. В некоторый момент черепахи начинают двигаться с одинаковыми по модулю скоростями. При этом каждая черепаха в любой момент времени движется в направлении той черепахи, на которую она смотрит. Определите время движения черепах до их встречи в центре квадрата.
Рис. 10
7. Начальные координаты тел 1 и 2 из упражнения 6 равны, соответственно, –10 м и 10 м. Определите координаты этих тел в моменты времени: а) 6 с; б) 8 с; в) 10 с.
Шаг 0. Выбор модели.
Будем считать мяч __________ телом, а его движение ______________ падением, поскольку влиянием воздуха следует пренебречь. Поэтому во время полёта ускорение мяча направлено __________________ и по модулю равно _________ За момент окончания полёта мяча примем момент, когда мяч вновь окажется в точке его отрыва от руки в момент броска.
Шаг 0. Выбор модели.
Шаг 0.
Будем считать мину ___________ телом, а её движение _______________ падением, поскольку влиянием воздуха можно пренебречь. Поэтому в любой момент времени ускорение мины направлено ______________ и по модулю равно _______.
Шаг 1.
Систему отсчёта свяжем с ___________. Начало отсчёта поместим в точку выстрела. Ось X направим горизонтально в направлении ______________. Ось Y направим _________________. Часы включим в момент ____________.
Шаг 2.
В выбранной системе отсчёта начальные координаты мины: х 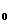 = _____, y
= _____, y 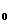 = _______.
= _______.
Шаг 3.
Проекции начальной скорости 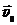 мины на координатные оси X и Y соответственно равны:
мины на координатные оси X и Y соответственно равны: 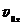 = ____________________________________________и
= ____________________________________________и 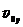 = ______________________________________.
= ______________________________________.
Шаг 4.
Ускорение 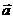 мины в любой момент времени равно ___ и направлено ______________________ оси Y. Поэтому проекции
мины в любой момент времени равно ___ и направлено ______________________ оси Y. Поэтому проекции  ускорения мины на оси X и Y равны:
ускорения мины на оси X и Y равны: 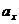 = ___;
= ___; 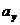 = _____. Движение мины вдоль оси X является _________________, а ее координата х изменяется по закону: x(t) = _______________________.
= _____. Движение мины вдоль оси X является _________________, а ее координата х изменяется по закону: x(t) = _______________________.
Так как проекция ускорения мины на ось Y _______________, координата мины вдоль оси Y изменяется по закону: y(t) = ________________________.
Шаг 4*.
Законы изменения проекций скорости мины от времени имеет вид:
υх (t) = ______________________, υy (t) = ______________________.
Шаг 5.
По условию задачи в момент времени tп падения мины на мишень координата у мины удовлетворяет уравнению: y(tп) = _____________________.
В этот момент проекция скорости мины на ось y равна:
υy(tп) = ________________________.
Время tм достижения максимальной высоты полёта определим из условия равенства нулю компоненты скорости мины вдоль оси ____: ___________________________________.
Шаг 6.
Система уравнений имеет вид:
y(t) = ________________________; (1) (закон движения по оси Y)
x(t) = ________________________; (2) (закон движения по оси X)
υy(t) = _______________________; (3) (закон изменения проекции скорости
вдоль оси Y)
υx(t) = _______________________; (4) (закон изменения проекции скорости
вдоль оси X)
y(tп) = _______________________; (5) (условие падения)
υy (tм) = ______________________; (6) (условие максимального подъёма)
Шаг 7. Решение системы уравнений.
Из уравнений (1) и (5) получим уравнение для расчета времени движения до попадания в мишень: _________________________________________.
Решение этого уравнения даёт два корня, отвечающие моментам времени прохождения миной уровня h. Попаданию в мишень соответствует больший из этих корней. Поэтому: tп = _____________________.
Подставляя это значение в уравнение (2), вычисляем дальность полёта мины по горизонтали (вдоль оси Х): L = _______________________________.
Подстановка полученного значения времени полёта tп мины в уравнение (3) позволяет вычислить проекцию скорости мины vy(tп) на ось Y в момент попадания в мишень: υy(tп) = _______________________________.
Модуль скорости мины в момент попадания в мишень определим из (3) и (4): υ(tп) = __________________________.
Угол φ между вектором скорости мины в момент tп и осью Х определим из соотношения: tgφ = _____________.
Из уравнений (7) и (3) найдём время подъёма мины на максимальную высоту:
tм = _____________________; а затем из (1), определим максимальную высоту подъёма мины: H = _____________________________________.
Ответ: Время полёта мины tп = _____________; в момент tп модуль скорости мины υ(tп) = _____________. Вектор скорости мины в этот момент образует с осью Х угол φ = _____.
Дальность полёта мины по горизонтали L = ___________, а максимальная высота подъёма мины H = _________.
 10. Камень, брошенный вертикально вверх, упал на Землю через t с. На каком расстоянии по горизонтали от точки бросания упадёт камень на Землю, если его бросить с той же начальной скоростью, но под углом a к горизонту?
10. Камень, брошенный вертикально вверх, упал на Землю через t с. На каком расстоянии по горизонтали от точки бросания упадёт камень на Землю, если его бросить с той же начальной скоростью, но под углом a к горизонту?
 11. Самолёт, летящий на высоте Н горизонтально со скоростью
11. Самолёт, летящий на высоте Н горизонтально со скоростью 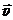 , сбрасывает груз. Под каким углом к горизонту штурман должен видеть место приземления груза в оптический прицел в момент сброса, чтобы обеспечить попадание?
, сбрасывает груз. Под каким углом к горизонту штурман должен видеть место приземления груза в оптический прицел в момент сброса, чтобы обеспечить попадание?
Рис. 11
1) только график а) 2) графики в) и г)
3) графики а) и г) 4) все
Отметьте знаком × правильный вариант ответа.
1) ÿ 2) ÿ 3) ÿ 4) ÿ
3. Определите начальный угол j0 и угловую скорость w пяти точечных тел, законы движения которых в СИ приведены в таблице.
| № | Закон движения | Начальный угол, рад | Угловая скорость, рад/с |
 | |||
 | |||
 | |||
 | |||
 |
4. Изобразите на окружностях (рис. 12) положения точечных тел, законы движения которых даны в задании 3, в моменты времени t, равные 0, 1, 2 и 3 с. Угол j отсчитывайте от оси X против хода часовой стрелки, если он положителен, и по ходу часовой стрелки, если он отрицателен.

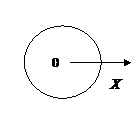


Рис. 12
5. Определите частоту n и период обращения Т для каждого из тел, законы движения которых даны в задании 3.
| Точечное тело | |||||
Частота обращения, n, с 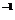 | |||||
| Период обращения, Т, с |
6. Точечное тело движется по окружности радиусом R = 1 м. Его положение в момент включения часов обозначено на рис. 13 жирной точкой. Угловая скорость тела  рад/с. Покажите на рисунке положение тела, как направлены его скорость (синим карандашом) и центростремительное ускорение (красным карандашом) через 1, 2, 4 и 8 с после начала движения. Чёрным карандашом изобразите векторы изменения скорости тела от момента начала движения до указанных моментов времени. Заполните таблицу, рассчитав пути, пройденные телом за указанные промежутки времени.
рад/с. Покажите на рисунке положение тела, как направлены его скорость (синим карандашом) и центростремительное ускорение (красным карандашом) через 1, 2, 4 и 8 с после начала движения. Чёрным карандашом изобразите векторы изменения скорости тела от момента начала движения до указанных моментов времени. Заполните таблицу, рассчитав пути, пройденные телом за указанные промежутки времени.
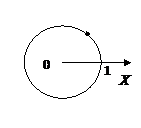
Рис. 13.
| t, с | < |
