Математическое ожидание и дисперсия

Математическим ожиданием дискретной случайной величины называется сумма вида:

М(Х) = x₁р₁ + x₂p₂ + ... + x_np_n = 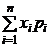, (2)

где x_i – возможные значения дискретной случайной величины;

p_i – вероятность появления значения x_i.

Свойства математического ожидания:

1. М(СХ) = СМ(Х); М(С) = С,

где С – произвольная постоянная величина.

2. М(Х₁Х₂···Х_n) = М(Х₁)М(Х₂)···М(Х_n),

если X₁, Х₂, ..., Х_n – взаимно независимые случайные величины.

3. М(Х₁ + Х₂ + ... + Х_n) = М(Х₁) + М(Х₂) + ... + М(Х_n).

4. М(Х) = nр,

где X – дискретная случайная величина;

n – число испытаний с биномиальным законом распределения;

р – вероятность появления события в одном испытании.

Математическое ожидание характеризует среднее значение случайной величины.

Рассеяние случайной величины около среднего значения характеризуют дисперсия и среднее квадратичное отклонение.

Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = М(Х – М(Х))².

Дисперсию целесообразно вычислять по формуле

D(X) = М(Х²) – (М(Х))². (3)

Свойства дисперсии:

1. D(C) = 0; D(CX) = C²D(X),

где С – произвольная постоянная.

2. D(Х₁ + Х₂ + ... + Х_n) = D(X₁) + D(X₂) + ... + D(X_n),

где X_i – независимые случайные величины.

3. D(X) = npq,

где X – дискретная случайная величина с биномиальным законом распределения;

n – число испытаний;

р, q – вероятность появления и вероятность непоявления события в одном испытании соответственно.

4. (Х) = ,

где (Х) – среднее квадратичное отклонение.

2.5. Даны законы распределения двух независимых случайных величин:

X
р	0,4	0,2	0,1	0,3
Y
Р	0,5	0,2	0,3

Найти математическое ожидание и дисперсию случайной величины Z = 2Х + 3Y.

Решение. Используя свойства математического ожидания и дисперсии, а также учитывая, что X и Y – независимые случайные величины, имеем:

M(Z) = М(2Х + 3Y) = М(2Х) + М(3Y) = 2М(Х) + 3М(Y);

D(Z) = D(2X + 3Y) = D(2X) + D(3Y) = 4D(X) + 9D(Y).

По формуле (2.2) вычислим М(X) и M(Y):

М(Х) = 2 · 0,4 + 4 · 0,2 + 6 · 0,1 + 8 · 0,3 = 4,6;

М(Y) = 0 · 0,5 + 1 · 0,2 + 2 · 0,3 = 0,8.

Тогда:

M(Z) = 2 · 4,6 + 3 · 0,8 = 11,6.

По формуле (2.3) вычислим D(X) и D(Y). Вначале найдем М(Х²) и M(Y²):

М(Х²) = 4 · 0,4 + 16 · 0,2 + 36 · 0,1 + 64 · 0,3 = 27,6;

М(Y²) = 0 · 0,5 + 1 · 0,2 + 4 · 0,3 = 1,4.

Затем определим D(X) и D(Y):

D(X) = M(X²) – (М(Х))² = 27,6 – 4,6² = 6,44;

D(Y) = M(Y²) – (М(Y))² = 1,4 – 0,8² = 0,76.

Окончательно получим

D(Z) = 4 · 6,44 + 9 · 0,76 = 32,6.

2.6. Два консервных завода поставляют продукцию в магазин в пропорции 2 : 3. Доля продукции высшего качества на первом заводе составляет 90 %, а на втором – 80 %. В магазине куплено 3 банки консервов. Найти математическое ожидание и среднее квадратичное отклонение числа банок с продукцией высшего качества.

Решение. Вначале составим закон распределения случайной величины X – числа банок с продукцией высшего качества среди купленных трех банок. Вероятность появления события А – куплена банка с продукцией высшего качества – найдем по формуле полной вероятности:

Р(А) = 0,9(2/5) + 0,8(3/5) = 0,84.

Закон распределения случайной величины X можно определить, используя формулу Бернулли:

.

Случайная величина X может принимать значения 0, 1, 2, 3. Закон ее распределения (с учетом того, что p = 0,84, q = 0,16) примет вид:

X
р	0,004	0,066	0,337	0,593

Тогда:

М(Х) = 0 · 0,004 + 1 · 0,066 + 2 · 0,337 + 3 · 0,593 = 2,519,

D(X) = 1 · 0,066 + 4 · 0,337 + 9 · 0,593 – 2,519² = 0,406,

.

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ