Теорема 3. Всякое бесконечное подмножество счетного множества также счетно.

Доказательство.

Пусть А – счетное множество и ВÌА также содержит бесконечное число элементов. Представим А в форме последовательности: А={a₁, a₂, a₃,…}. Будем рассматривать элементы множества А по порядку, то есть а₁, затем а₂, а₃ и т.д. При этом мы иногда будем «наталкиваться» на элементы подмножества В. Будем ставить этим элементам множества В в соответствие «номер встречи с ним». Тем самым, будет установлено взаимно-однозначное соответствие между В и N, что и говорит о счетности В.<

Суть теорем 2 и 3 можно сформулировать так: счетное множество есть самое маленькое из всех бесконечных множеств.

Теорема 4. Сумма конечного числа счетных множеств есть также счетное множество.

Доказательство.

Пусть для простоты имеются два счетных множества А и В.

А={a₁, a₂, a₃,…}.

В={b₁, b₂, b₃,…}.

Представим их сумму в виде

АÈВ={a₁, b₁, a₂, b₂, a₃, b₃,…}.

Из теоремы 1 следует, что АÈВ есть счетное множество.

Однако есть одна тонкость: дело в том, что в множествах А и В могут быть одинаковые элементы, которые надо оставить по одному разу. Но после того, как мы это сделаем, все равно останется бесконечное множество, и, по теореме 3, оно будет счетным.<

Замечание. Заметим, что представление АÈВ в виде

АÈВ={a₁, а₂, a₃, … b₁, b₂, b₃,…} не доказывало бы нашу теорему. Почему?

Теорема 5 Сумма счетного числа конечных множеств есть конечное или счетное множество.

Доказательство.

Пусть множества А_i, 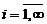имеют вид

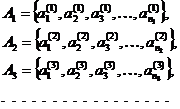(обратите внимание на нумерацию элементов)

Представим 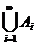в виде

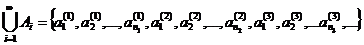
Мы получили последовательность. Оставляя совпадающие во множествах А_i элементы только по одному разу, мы получим или конечное множество или бесконечное. Но по теореме 3 это бесконечное подмножество может быть только счетным. <

Теорема 6. Сумма счетного числасчетных множеств есть также счетное множество.

Доказательство.

Пусть А_i, 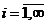есть счетные множества

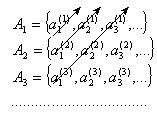
и этих множеств счетное число. Представим 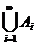в форме последовательности, используя так называемый прием диагонализации:

.

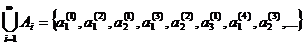Оставляя повторяющиеся в различных множествах элементы по одному разу, мы получим снова бесконечное множество, которое по теореме 3 будет также счетным.

В заключение этого раздела небольшая задача. Был (а может и есть) польский писатель-фантаст Станислав Лем, произведения которого посвящены теме космоса («Солярис», «Возвращение со звезд», «Эдем»). Среди них есть сборник рассказов «Звездные дневники Иона Тихого». Ион Тихий - это космический барон Мюнхгаузен, который на своей ракете шастает по всей Галактике, попадая при этом в самые невероятные ситуации (например, дерется сам с собой, попав в петлю времени), из которых он всегда выходит с честью.

Так вот, прилетает Ион Тихий в межгалактическую гостиницу. В ней счетное число номеров, и все номера заняты. Ион Тихий обращается к портье, и тот все-таки селит его в эту гостиницу, причем никого из прежних постояльцев не выгоняет. Как поступил портье?