Раскрытие неопределенностей других видов

Если мы имеем неопределенности следующих видов: , то все они путем алгебраических преобразований приводятся к виду , для которых можно воспользоваться правилом Лопиталя. Пусть

.

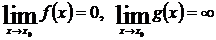Тогда имеем:

.

Второе из этих выражений представляет при х ® х₀ неопределенность вида 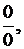третье – неопределенность вида .

Пример 1. .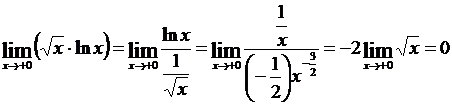

Есл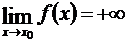и и 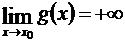, то выражение 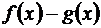можно привести, например, к неопределенности вида 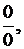путем следующих преобразований:

.

Часто, впрочем, найти предел этого выражения удается проще.

Пример 2.

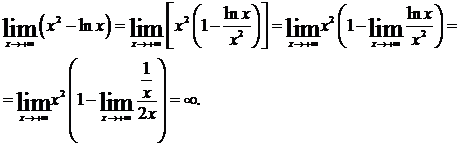
В случае неопределенных выражений вида рекомендуется предварительно прологарифмировать.

Пусть и в окрестности точки х₀ 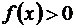, тогда

.

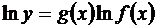Предел представляет собой неопределенность уже изученного типа 0·¥ (или ¥·0). Допустим, что одним из указанных выше приемов удается найти

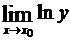, который оказывается равным конечному числу т, +¥ или –¥. Тогда , соответственно, будет е^т,+¥ или 0.

Пример 3. Вычислить 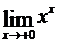. Положив у = х^х, находим:

.

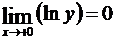Следовательно, , откуда , т.е. .

Пример 4.

Пусть 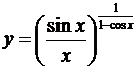. Требуется найт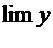и при (неопределенность вида ).

Если считать х > 0 (этим предположением, ввиду четности функции у, можно ограничиться), то

.

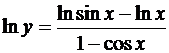Пользуясь последовательно дважды правилом Лопиталя, получим:

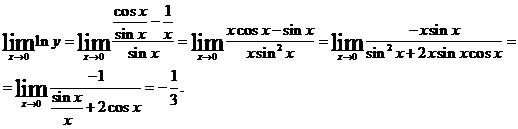
Откуда .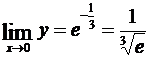

Заметим, что не все неопределенности можно раскрыть с помощью правила Лопиталя. Например,

.

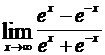Однако этот предел можно найти другим способом. Действительно, разделив заданную дробь на е^х, получим:

.

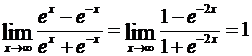Формула Тейлора

Устанавливаемая в этом параграфе формула является одной из основных формул математического анализа и имеет многочисленные приложения, как в анализе, так и в смежных дисциплинах. Данная формула устанавливает способ приближенного отображения, или, как говорят, способы аппроксимации произвольной функции с помощью полиномов (многочленов), которые являются наиболее простыми среди всех других функций.

Предположим, что функция 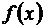имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х₀. Найдем многочлен Р_п(х) степени не выше п, значение которого в точке х₀ равняется значению функции 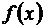в этой точке, а значения его производных до п-го порядка в точке х = х₀ равняются значениям соответствующих производных от функции 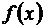в этой точке.

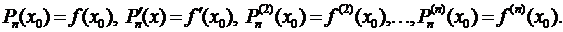(3.43)

Естественно ожидать, что такой многочлен в некотором смысле «близок» к функции .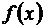

Будем искать этот многочлен в форме многочлена по степеням (х – х₀) с неопределенными коэффициентами

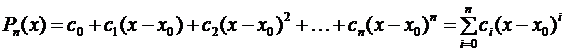(3.44)

Неопределенные коэффициенты c_i, i = 0, 1, 2, …, п определим так, чтобы удовлетворялись условия (3.43).

Предварительно найдем производные от Р_п(х):

(3.45)

Подставляя в левые и правые части равенств (3.44) и (3.45) вместо х значение х₀и заменяя на основании равенств (3.43) Р_п(х₀) через 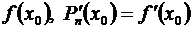и т.д., получим:

Подставляя найденные значения с_i в формулу (3.44), получим искомый многочлен: 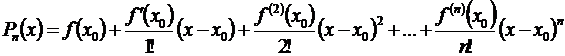. (3.46)

Многочлен (3.46) называют многочленом Тейлора для функции 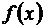. Обозначим через R_n+1(х) разность значений данной функции 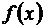и построенного многочлена P_n(x): R_n+1(х) = 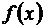– P_n(x).

Откуда 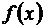= P_n(x) + R_n+1(х), или, в развернутом виде:

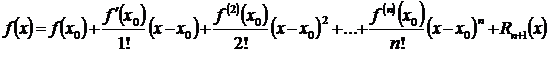. (3.47)

Выражение (3.47) называют формулой Тейлора для функции 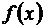в окрестности точки х₀, а R_n+1(х) – остаточным (дополнительным) членом формулы Тейлора. Для тех значений х, для которых остаточный член R_n+1(х) мал, многочлен P_n(x) дает приближенное значение функции .

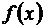Таким образом, формула (3.47) дает возможность заменить функцию

у = 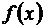многочленом у = P_n(x) с соответствующей степенью точности, равной значению остаточного члена R_n+1(х). Можно показать, что такое представление функции 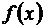единственно, т.е., что, если имеем одновременно, вблизи х₀,

,

,

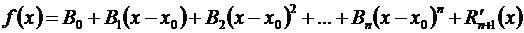то необходимо А₀ = В₀, А₁ = В₁,…, А_п = В_п.

Для остаточного члена получено довольно много различных форм представления, одно из которых имеет вид:

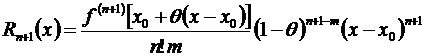, (3.48)

где т – произвольное положительное число, 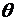– число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.

Из него, придавая т конкретные значения, можно получить более частные формы остаточного члена. Положив т = п + 1, получим остаточный член в форме Лагранжа:

. (3.49)

Он напоминает следующий очередной член формулы Тейлора, лишь вместо того, чтобы вычислять (п + 1)-ю производную в точке х₀, эту производную берут для некоторого среднего (между х₀ и х) значения .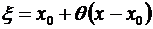

При т = 1 приходим к остаточному члену в форме Коши.

(3.50)

Так как формы Лагранжа и Коши отвечают разным значениям m, а θ зависит от m, то значения θ в формулах (3.49) и (3.50) является, вообще говоря, различными. Обе формы остаточного члена (Лагранжа и Коши) обычно используются в тех случаях, когда требуется при тех или иных фиксированных значениях х, отличных от х₀, приближенно вычислить функцию 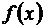с наперед указанной степенью точности, которую можно оценить по формулам (3.49) и (3.50) для данного х, а также воздействовать на нее за счет изменения n. Наряду с этим встречаются задачи в которых нас интересует не численная величина указанной ошибки, а лишь порядок ее относительно малой величины (х – х₀). Для этой цели удобна форма записи остаточного члена в виде

. (3.51).

Данная формула означает, что при стремлении х к х₀ остаточный член представляет собой бесконечно малую порядка выше n-го по сравнению с (х – х₀), т.е. 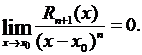Равенство (3.51) называют остаточным членом, представленным в форме Пеано.

Формулу Тейлора (3.47) часто записывают в несколько ином виде. Положив в (3.47) (х – х₀) = Δх, х = х₀ + Δх и f (х) – f (х₀) = Δf (х₀) получаем

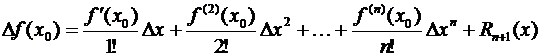(3.52)

с точностью до дополнительного члена, таким образом, приращение функции разложено по степеням приращения независимой переменной.

Далее, вспоминая, что

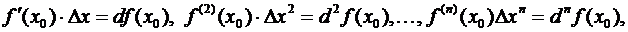
мы можем переписать (3.52) в такой форме

Здесь остаточный член записан в форме Пеано. Отсюда видим, что при 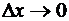последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно ) в разложении бесконечно малого приращения функции.

Если в (3.52) остаточный член записать в форме Лагранжа (3.49), то формула Тейлора (3.52) с остаточным членом в форме Лагранжа (3.49) является естественным обобщением формулы Лагранжа (3.34). Формула Лагранжа (3.34) конечных приращений получается из формулы (3.52) в частном случае n = 0.