Основные теоремы дифференциального исчисления

4.1. Теорема Ролля (теорема о корнях производной)

Теорема Ролля.Если функция y = f(х):1) определена и непрерывна на сегменте [a,b],2) дифференцируема в каждой точке интервала (a,b),3) на концах сегмента принимает равные значения f (a) = f (b),то внутри сегмента [a,b]найдется по крайней мере одна точка ξ,производная в которойf ′(ξ)равна нулю.

С геометрической точки зрения это означает, что внутри сегмента найдутся такие точки ξ,что касательная к кривой в этих точках параллельна оси Ох (рис.18).

Доказательство.Так как функция f(х)непрерывна на отрезке [a,b],то, по 2-ой теореме Вейерштрасса (гл.1, §12, п.12.9), она имеет на этом отрезке наибольшее значение Ми наименьшее значение m(рис.18).

Если M= m, то функция f(х)при всех значениях хиз промежутка [a,b]имеет постоянную величину f(х) = f(a) = f(b) = М.Но тогда в любой точке отрезка будет f ′(x) = 0, и теорема доказана.

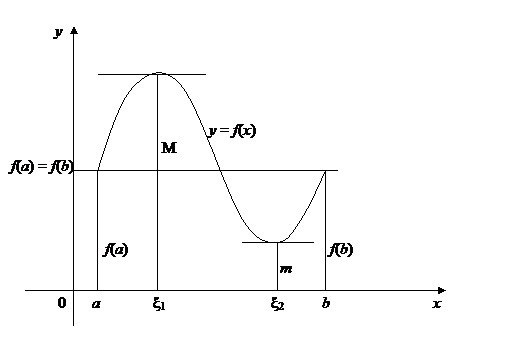
Рис. 18

Предположим, что M ¹m. Мы знаем, что оба эти значения функцией достигаются, но, так как f(a) = f(b),то хоть одно из них достигается в некоторой точке ξмежду аи b.Для определенности предположим, что f(ξ) = М.Тогда, так как f(ξ)– наибольшее значение функции, то f(ξ + Dx) – f(ξ) £ 0как при Δх >0, так и при Dx <0.

Отсюда следует, что

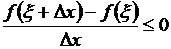при Dx>0,

при Dx<0.

Так как по условию теремы производная при х = ξсуществует, то, переходя к пределу при Dx ®0, получим

при Dx>0,

при Dx<0.

Но соотношения f ′(ξ)≤ 0 иf ′(ξ)≥ 0 совместимы лишь в том случае, еслиf ′(ξ) = 0. Следовательно, внутри отрезка [a,b]имеется точка ξ,в которой производнаяf ′(ξ) = 0.

Замечания: 1. Из доказательства теоремы Ролля вытекает справедливость следующего утверждения, которое носит название теоремы Ферма.

Теорема Ферма. Пусть функция f(х)определена в некотором промежутке [a,b]и во внутренней точке xэтого промежутка принимает наибольшее (наименьшее) значение. Если существует конечная производная f ′(ξ) в этой точке, то необходимо f ′(ξ) = 0.

2. Точек, в которых производная функции равна нулю, может быть больше одной.

Например, функция у = sin х:

1) на сегменте [0,2p]непрерывна

2) имеет производную на интервале (0,2p);

3) f (0) = f (2p) = 0;

у' = cosx, cosx = 0, при .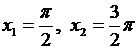

Таким образом, на [0,2p] имеются две точки , в которых f '(x) = 0.

3. Если функция не удовлетворяет хотя бы одному из трех условий теоремы, то теорема не выполняется.

Например, функция xÎ[-1,1],

1) непрерывна на сегменте [-1,1], 2) f (-1) = f (1) = 1,

Но в точке х = 0 заданная функция производной не имеет. Для этой функции теорема Ролля на [-1,1] не выполняется.

4.2. Формула Лагранжа (формула конечных приращений)

Большое значение в анализе и его приложениях имеет следующая теорема, принадлежащая Лагранжу.

Теорема Лагранжа. Если функция у = f(х):

1) непрерывна на сегменте [a,b],

2) дифференцируема в каждой точке интервала (a,b), то внутри сегмента [a,b] существует, по крайней мере, одна такая точка ξ, что справедлива формула

где а < ξ < b. (3.31)

Формулу (3.31) которую обычно записывают в виде

(3.32)

называют формулой Лагранжа или формулой конечных приращений. Подчеркнем, что в формуле (3.31) и (3.32) не обязательно считать, что b > a.

Геометрическая интерпретация теоремы дана на рис.19. Отношение равно угловому коэффициенту k = tga секущей, проходящей

через точки А(а, f(a)) и В(b, f(b)) кривой у = f(х),а есть угловой коэффициент касательной к кривой у = f(х), проходящей через точку С(ξ, f(ξ)). Формула Лагранжа (3.31) означает, что на кривой у = f(х)между точками А и В найдется такая точка С, касательная в которой параллельна секущей АВ.

Рис. 19

Заметим, что теорема Ролля является частным случаем теоремы Лагранжа (при f(а) = f(b) и касательной параллельной оси Ох). Теорему Лагранжа называют также теоремой о среднем значении (в дифференциальном исчислении).

Доказательство. Рассмотрим на сегменте [a,b] следующую вспомогательную функцию:

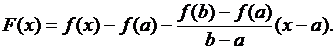(3.33)

Эта функция удовлетворяет всем условиям теоремы Ролля. В самом деле, она непрерывна в [a,b], так как представляет собой разность между непрерывной функцией f(х) и линейной функцией. В интервале (a,b) она имеет определенную конечную производную, равную

Наконец, непосредственной подстановкой в формулу (3.33) убеждаемся, что 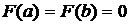, т.е. F(x) принимает равные значения на концах промежутка.

Следовательно, к функции F(x) можно применить теорему Ролля и утверждать существование в (a,b) такой точки ξ, что 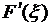= 0. Таким образом, 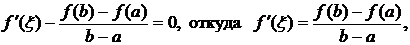что и требовалось доказать.

Часто удобно бывает записывать формулу Лагранжа в виде, несколько отличном от (3.32). Пусть f(x) удовлетворяет условиям теоремы Лагранжа. Зафиксируем любое х₀ из сегмента [a,b] и зададим ему приращение Δх произвольное, но такое чтобы значение (х₀+Δх) также лежало на сегменте [a,b]. Применим формулу Лагранжа к сегменту [х₀, х₀ +Δх] при Δх > 0. Число ξ, заключенное в этом случае между х₀ и х₀ + Δх, можно представить так: , где 0 < θ < 1. Тогда формула Лагранжа примет вид:

или 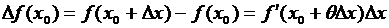(0 < θ <1). (3.34)

Формула Лагранжа в виде (3.34) дает точное выражение для приращения функции через вызвавшее его произвольное конечное приращение Δх аргумента. Отсюда проистекает и самое название «формула конечных приращений». Эта формула противопоставляется приближенному равенству (§2, п.2.1):

относительная погрешность которого стремится к нулю лишь при бесконечно малом Δх. Некоторым неудобством формулы Лагранжа является то, что в ней фигурирует неизвестное нам число 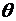(или 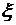). Это не мешает, однако, многообразным применением этой формулы в анализе. В качестве примера рассмотрим следующие утверждения, справедливость которых непосредственно вытекает из формулы Лагранжа.

Условие постоянства функции

Теорема.Если функция f(x) дифференцируема на интервале (a,b) и если всюду на этом интервале 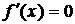, то функция f(x) является постоянной на интервале (a,b).

Доказательство. Пусть х₀ – некоторая фиксированная точка интервала (a,b), а х – любая точка этого интервала.

Сегмент [х₀,х] целиком принадлежит интервалу (a,b). Поэтому функция f(x) дифференцируема (а стало быть и непрерывна) всюду на сегменте [х₀,х]. Это дает право применить к функции f(x) на сегменте [х₀,х] теорему Лагранжа. Согласно этой теореме внутри сегмента [х₀,х] найдется точка ξ такая, что

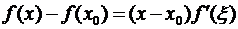. (3.35)

По условию производная функции f(x), равна нулю всюду в интервале (a,b). Стало быть, 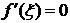и из формулы (3.35) получаем 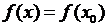. Это и означает, что функция f(x) постоянна всюду на интервале (a,b).

Данное утверждение имеет простой геометрический смысл: если касательная в каждой точке некоторого участка кривой у = f(x) параллельна оси Ох, то указанный участок кривой у = f(x) представляет собой отрезок прямой, параллельный оси Ох.