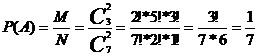Практическая работа №2: «Решение задач по комбинаторике».

Комбинаторными задачами называются задачи, в которых необходимо подсчитать, сколькими способами можно сделать тот или иной выбор, выполнить какое-либо условие.

Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, состоящее из k элементов, называется размещением из n элементов по k элементов:

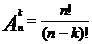, где n!=1*2*3*…*n

Пример.Группа учащихся изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 4 различных урока?

Решение.Число способов равно числу размещений из 7 элементов по 4, т.е. равно 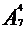. Получаем = .

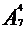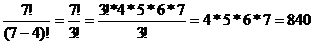Размещения из n элементов по n элементов называются перестановками из n элементов:

.

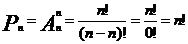Пример.Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?

Решение.Цифра 5 обязана стоять на последнем месте. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е. 5!=5*4*3*2*1=120.

Сочетания. Пусть имеется множество, состоящее из n элементов. Каждое его подмножество, содержащее k элементов, называется сочетанием из n элементов по k элементов:

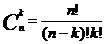
Пример.Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?

Решение.Матчей состоится столько, сколько существует двухэлементных подмножеств у множества, состоящего из 16 элементов, т.е. их число равно .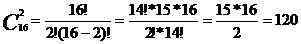

Свойства сочетаний:

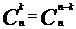
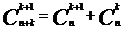
Практическая работа №3 «Вычисление вероятностей событий по классической формуле определения вероятностей».

Классическое определение вероятности: вероятность Р(А) события А равна отношению числа возможных результатов опыта (М), благоприятствующих событию А, к числу всех возможных результатов опыта (N):

.

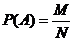Пример 1.Подбрасывание игральной кости один раз. Событие А состоит в том, что выпавшее число очков – чётно. В этом случае N=6 – число граней куба; М=3 – число граней с чётными номерами; тогда Р(А)=3/6=1/2.

Пример 2.Подбрасывание симметричной монеты 2 раза. Событие А состоит в том, что выпало ровно 2 герба. В этом случае N=4, т.к. 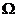={ГГ, ГР, РГ, РР}; М=1, т.к. А={ГГ}. Тогда Р(А)= ¼.

Пример 3.Вытягивание шара из урны, содержащей 2 белых и 3 чёрных шара. Событие А состоит в том, что вытянули чёрный шар. В этом случае N=2+3=5 (общее число шаров в урне), М=3 (число чёрных шаров), тогда Р(А)=3/5.

Пример 4.Набирая номер телефона, абонент забыл две последние цифры. Какова вероятность того, что он с первого раза наберёт эти цифры правильно, если он помнит, что они различны?

Решение.Обозначим А – событие, состоящее в том, что абонент, набрав произвольно две цифры, угадал их правильно. М – число правильных вариантов, очевидно, что М=1; N – число различных цифр, 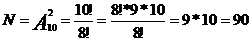. Таким образом, Р(А)=M/N=1/90.

Пример 5.Шесть шариков случайным образом располагаются в шести ящиках так, что для каждого шарика равновероятно попадание в любой ящик и в одном ящике может находиться несколько шариков.Какова вероятность того, что в каждом ящике окажется по одному шарику?

Решение.Событие А – в каждом ящике по одному шарику. М – число вариантов распределения шариков, при которых в каждый ящик попадает по одному шарику, М=6! (число способов переставить между собой 6 элементов). N – общее число вариантов N=6⁶ (так как каждый шарик может попасть в каждый из ящиков). В результате получаем .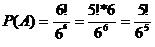

Пример 6.В урне 3 белых и 4 чёрных шара. Из урны вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение.Обозначим: А – событие, состоящее в появлении белых шаров; N – число способов вытащить 2 шара из 7; 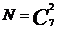; M – число способов вытащить 2 белых шара из имеющихся 3 белых шаров; .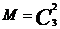