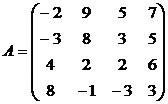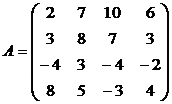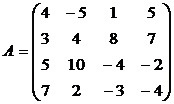Антагонистические матричные игры с нулевой суммой, имеющие решение в чистых стратегиях.

Для того чтобы решить игру в чистых стратегиях, необходимо найти оптимальные чистые стратегии игроков и выигрыш.

Определение. Пара 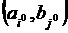называется седловой точкой функции 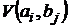при решении игры в чистых стратегиях, если

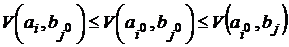, для .

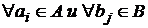Понятие седловой точки является ключевым понятием в теории игр. Таким образом, антагонистическая игра задается совокупностью 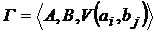. Если игроки выбрали в качестве стратегий компоненты 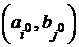седловой точки, то каждому из них невыгодно отклоняться от выбранной стратегии. Поэтому седловая точка является формализацией концепции равновесия в игре.

Определение. Говорят, что антагонистическая игра Г имеет решение, если функция 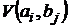имеет на декартовом произведении A×B седловую точку.

Пусть 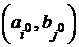— седловая точка игры. Тройка 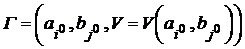называется решением игры, 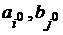– оптимальными стратегиями игроков, а V – значением игры. Возникают два основных вопроса: когда антагонистическая игра в чистых стратегиях имеет решение, т.е. имеет седловую точку и выигрыш в этой точке и как искать эти точки и выигрыш.

Рассмотрим игру Г с позиции сначала первого игрока, а затем с позиции второго.

Итак, первому игроку соответствуют строки платежной матрицы, они нас и будут интересовать в данном случае. Мы уже говорили, что игра рассматривается по отношению к первому игроку, то есть игрок A всегда выигрывает.

Шаг 1. Гарантированный результат игрока A. Рассмотрим стоки матрицы 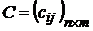и выберем в каждой стоке минимальный элемент:

.

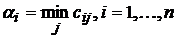Величины 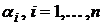являются гарантированными результатами для первого игрока, при выборе той или иной стратегии. Так как игрок A стремиться максимизировать свой выигрыш, то гарантированный результат показывает, что меньше суммы 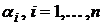игрок точно не получит, если применит свою i-ю стратегию.

Шаг 2. Максимальный гарантированный результат игрока A. Так как первый игрок стремиться максимизировать свой выигрыш, то среди всех своих гарантированных результатов он будет выбирать тот, который принесет ему максимальный гарантированный результат:

.

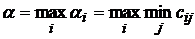Значение 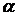называют нижней ценой игры и обозначают 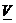. Та стратегия, которая соответствует максимальному значению 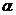и будет оптимальной для первого игрока.

Оптимальная стратегия 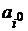первого игрока называется максиминной,

Теперь рассмотрим игру с позиции второго игрока B. Он стремиться минимизировать свой проигрыш.

Шаг 1. Гарантированный результат игрока B. Второму игроку соответствуют столбцы матрицы, и он будет выбирать наибольший элемент в каждом столбце:

,

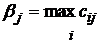это и будет его гарантированный результат, т.е. больше этого он уже точно не проиграет.

Шаг 2. Максимальный гарантированный результат игрока B. Среди всех своих гарантированных результатов второй игрок будет выбирать тот, который принесет ему меньший проигрыш:

.

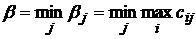Значение 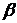называют верхней ценой игры и обозначают 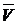. Так стратегия, которая соответствует минимальному значению 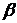для второго игрока и будет для него оптимальной.

Оптимальная стратегия 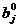второго игрока называется минимаксной.

Лемма. В любой антагонистической игре Г справедливо неравенство .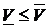

Доказательство. Возьмем произвольные стратегии игроков 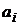и 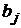. Тогда

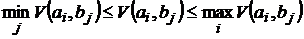
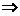
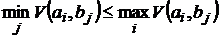
Левая часть последнего неравенства зависит от 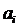, а правая часть – нет. Поэтому

.

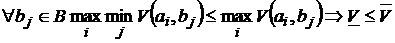Если 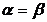, то говорят, что игра имеет решение в чистых стратегиях. Седловая точка игры будет 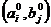и выигрыш .

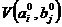Рассмотрим в общем виде решение игры в чистых стратегиях. Дана платежная матрица. Строкам соответствуют стратегии первого игрока, а столбцам – второго. Справа выпишем столбец 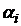минимальных элементов в строках и из всех элементов данного множества выберем максимальный элемент. Пусть это будет элемент 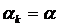. Тогда оптимальной стратегией первого игрока будет его k-я стратегия.

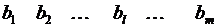
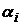
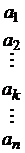
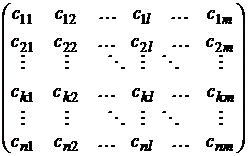
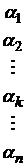
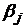
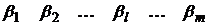
Внизу найдем 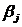и запишем их под столбцами, то есть максимальные элементы в каждом столбце и среди них найдем минимальный. Пусть это будет 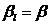. Тогда оптимальной стратегией второго игрока будет l-я стратегия.

Если 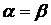, то седловая точка при решении игры в чистых стратегиях существует и в дано игре она составляет пару 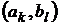выигрыш в ней равен 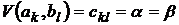. Седловая точка может быть не единственной и тогда выигрыш одинаков во всех точках.

Пример. Найти седловую точку и выигрыш при решении игры в чистых стратегиях для матрицы

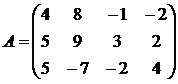
Шаг 1. В соответствии с алгоритмом, выберем в каждой строке минимальный элемент и получим вектор 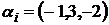. Среди этих значений найдем максимальное, это и будет нижней ценой игры 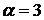. Так как данный элемент соответствует второй стратегии первого игрока, то она и будет для него оптимальной, т.е. игрок A выбирает стратегию .

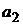Шаг 2. В соответствии с алгоритмом, выберем в каждом столбце максимальный элемент и получим вектор 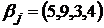. Среди этих значений найдем минимальное, это и будет верхней ценой игры 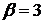. Так как данный элемент соответствует третьей стратегии второго игрока, то она и будет для него оптимальной, т.е. игрок B выбирает стратегию .

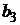Так как в данной игре 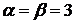, то седловая точка игры существует и .

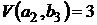Задачи для самостоятельного решения.

Найти решение игры в чистых стратегиях:

1. 2. .3.

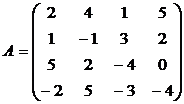
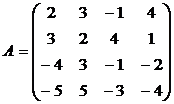
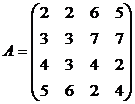
4. 5. 6.

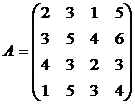
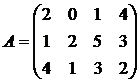
7. 8. 9.

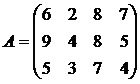
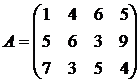
10. 11. 12.

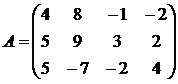
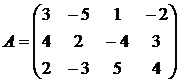
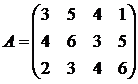
13. 14. 15.

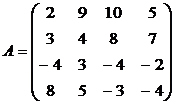
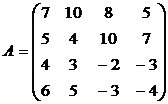
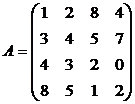
16. 17. 18.