Константу можно выносить за знак производной
Константу можно выносить за знак производной
Пример 1.1. y = 12sinx +17cosx + 99tgx
► Пользуясь правилом суммы и вынося константу за знак производной получаем
(12sinx + 17cosx + 99tgx)` = 12cosx – 17sinx +  ◄
◄
Пример 1.2. y = 11x101 +18 ln(x)
► y` = 1111x100 + 18/x◄
1)  ( 2sinx + 3cosx – 4xa+5 ax ) ( 2sinx + 3cosx – 4xa+5 ax ) | 2)  ( 3tgx + 3ctgx – 7ln(6x)+4 ax ) ( 3tgx + 3ctgx – 7ln(6x)+4 ax ) |
3)  ( 7arctgx + 5arcctg2x – 3log3(9x) ) ( 7arctgx + 5arcctg2x – 3log3(9x) ) | 4)  ( 6tgx + 3arcsinx – 7log5(7x) ) ( 6tgx + 3arcsinx – 7log5(7x) ) |
5)  ( 5tgx + 44arcsinx – 8log58(6x) ) ( 5tgx + 44arcsinx – 8log58(6x) ) | 6)  ( 32arctgx + 3ctgx – 4log6(6x) ) ( 32arctgx + 3ctgx – 4log6(6x) ) |
7)  ( 3sin2x + 5arcctgx – ln(6x) + 6x ) ( 3sin2x + 5arcctgx – ln(6x) + 6x ) | 8)  ( 23cosx + 78tgx – 99log3(6x)) ( 23cosx + 78tgx – 99log3(6x)) |
9)  (7secx + 5cosecx – 4og3(3x) + 7x ) (7secx + 5cosecx – 4og3(3x) + 7x ) | 10)  (7arcsinx + 9sinx – 3ln(x) + 2x ) (7arcsinx + 9sinx – 3ln(x) + 2x ) |
11)  ( 39cosx + 7arccosx –33 ax ) ( 39cosx + 7arccosx –33 ax ) | 12)  (4tgx + 45arcctgx – 87 ax ) (4tgx + 45arcctgx – 87 ax ) |
13)  ( 6arcsinx + 4ctgx – 6ln(x) + vx ) ( 6arcsinx + 4ctgx – 6ln(x) + vx ) | 14)  (5tgx + 2sinx – 56ln(6x) +x) (5tgx + 2sinx – 56ln(6x) +x) |
15)  ( 7arcctgx + cosx – 7ln(6x)+a 7x ) ( 7arcctgx + cosx – 7ln(6x)+a 7x ) | 16)  (1279x3 + 1279) (1279x3 + 1279) |
17)  (17chx + 34shx + 136th2x) (17chx + 34shx + 136th2x) | 18)  (28/4(sin(cos34x))) (28/4(sin(cos34x))) |
19)  (4xlnx + 88cos(lnx)) (4xlnx + 88cos(lnx)) | 20)  (24e3x + 3e21x) (24e3x + 3e21x) |
21)  (324x3 + 456x2 + 43x) (324x3 + 456x2 + 43x) | 22)  (77arccos(thx) + 99) (77arccos(thx) + 99) |
23)  (98tg3x + 84th5x) (98tg3x + 84th5x) | 24)  (354esinx + 945ecosx) (354esinx + 945ecosx) |
25)  (35cos(log3017x) + 92arctg5x) (35cos(log3017x) + 92arctg5x) | 26)  (73(2)3x + 198e45x) (73(2)3x + 198e45x) |
27)  (23earccos(x2) + (17e/2)arctgx) (23earccos(x2) + (17e/2)arctgx) | 28)  (73lnx3 + 3xlnx) (73lnx3 + 3xlnx) |
29)  (77th(arctgx)+356 (77th(arctgx)+356 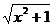 ) ) | 30)  (876ln (876ln 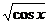 -126cos(79x)) -126cos(79x)) |
Производная от частного. Найти производную функции
Пример 2.1. y = (99x/sinx).
► Воспользуемся формулой ((u/v)` = (u`v – uv`)/v2)
(99x/sinx)`=99(1×sinx–xcosx)/sin2x. ◄
Пример 2.2. y = 3ax/lnx.
► Пользуясь правилом дифференцирования частного двух функций, получаем (3ax/lnx)` = 3(axlnalnx–3ax/x)ln2x. ◄
1)  (tg(x) /cx3)) 2)
(tg(x) /cx3)) 2)  (sin(x) /x) 3)
(sin(x) /x) 3)  (cos(x) /x5)
(cos(x) /x5)
4)  (arctg(x) /4x) 5)
(arctg(x) /4x) 5)  (arcctg(x) /(x-x8)) 6)
(arcctg(x) /(x-x8)) 6)  (arcsin(x) /5x))
(arcsin(x) /5x))
7)  (arccos(x) /ax) 8)
(arccos(x) /ax) 8)  (5x/ln(x)) 9)
(5x/ln(x)) 9)  (log(x) /x3x))
(log(x) /x3x))
10)  (ln(x) /cosec(x)) 11)
(ln(x) /cosec(x)) 11)  (xa/sec(x)) 12)
(xa/sec(x)) 12)  (x2/arccos(x))
(x2/arccos(x))
13)  (4x5) /arcsin(x)) 14)
(4x5) /arcsin(x)) 14)  (9x) /arctg(x)) 15)
(9x) /arctg(x)) 15)  (12x) /arcctg(x))
(12x) /arcctg(x))
16) 
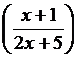 17)
17) 
 18)
18) 

19) 
 20)
20) 
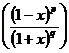 21)
21) 

22) 
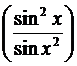 23)
23) 
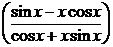 24)
24) 

25) 
 26)
26) 
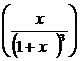 27)
27) 

28)  (lg4x/thx) 29)
(lg4x/thx) 29)  (chx/(1-shx2)) 30)
(chx/(1-shx2)) 30)  (shx/(1-thx))
(shx/(1-thx))
Производная произведения
Пример 3.1. y = xsinxex.
► Пользуясь формулой (uv)` = u`v + uv` получим
(*) (xsinxex)` = xex cosx + exsinx(x + 1)
Здесь удобно взять u = xex,а v = sinx.Так как u – произведение двух функций, x и ex, то воспользуемся формулой для вычисления произведения двух функций
u` = u1`v1+u1v1` = ex(x + 1), где u1 = ex, v1 = x.
Подставляя найденное u` и v` = cosx получим (*)◄
Пример 3.2. y = sinxcosx(ax)
► Действуя по аналогии с примером 3.1. возьмем u = sinxcosx и v = ex, тогда
u` = cos2x-sin2x = cos2x, v` = ex
По формуле для производной произведения получим
(sinxcosxex)` = u`v + uv` = excos2x + exsinxcosx = ex(cos2x + (sin2x)/2) ◄
1)  ( 2xlog25x(-x56)) 2)
( 2xlog25x(-x56)) 2)  ( 4xsinx(-arctg(x))) 3)
( 4xsinx(-arctg(x))) 3)  (3xtgx(-arccos(x)))
(3xtgx(-arccos(x)))
4)  ( 5xctgx(-x5a)) 5)
( 5xctgx(-x5a)) 5)  ( axlog2x(-x7)) 6)
( axlog2x(-x7)) 6)  (7xlog4x(-x3))
(7xlog4x(-x3))
7)  ( 8axlog7x(-x9)) 8)
( 8axlog7x(-x9)) 8)  ( 9xlog3x(-5x8)) 9)
( 9xlog3x(-5x8)) 9)  (343xlog21x(-x33))
(343xlog21x(-x33))
10)  ( 77xlog63x(-4x8)) 11)
( 77xlog63x(-4x8)) 11)  ( 22xlog23x(-xa)) 12)
( 22xlog23x(-xa)) 12)  (2xcosx(-x3))
(2xcosx(-x3))
13)  ( 6xlog67x(-x66)) 14)
( 6xlog67x(-x66)) 14)  ( 9xlog55x(-x77)) 15)
( 9xlog55x(-x77)) 15)  (757xlog44x(-x88))
(757xlog44x(-x88))
16)  (xsinx) 17)
(xsinx) 17)  (xshx) 18)
(xshx) 18)  (xthx3)
(xthx3)
19)  (tgxthx) 20)
(tgxthx) 20)  (lnxchx) 21)
(lnxchx) 21)  (sinx arccos2x)
(sinx arccos2x)
22)  (e2xarctgxchx) 23)
(e2xarctgxchx) 23)  (axxb) 24)
(axxb) 24)  (arcctgxlog32x3)
(arcctgxlog32x3)
25)  (x3tgxsin3x) 26)
(x3tgxsin3x) 26)  (23xln(x2+3x+2)) 27)
(23xln(x2+3x+2)) 27)  (shx(ax+b))
(shx(ax+b))
28)  (tgxarcctg24x) 29)
(tgxarcctg24x) 29)  (sin12x5chx7) 30)
(sin12x5chx7) 30)  (exxaln(bx)4)
(exxaln(bx)4)
Производная сложной функции
Пример 4.1. y = log3(arcsinx)
► Пользуясь правилом нахождения производной от сложной функции и полагая f=log3(g), g=arcsinx, найдем f`(g) и g`(x).
f`(g) = log3e/g, g`(x)=  , (f(g(x)))`=f`(g)g`(x) Þ
, (f(g(x)))`=f`(g)g`(x) Þ
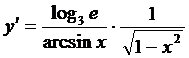 ◄
◄
Пример 4.2. 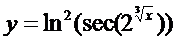
► Поступаем, аналогично предыдущему примеру
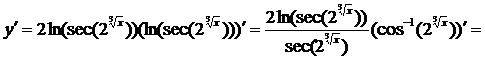

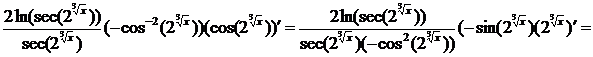
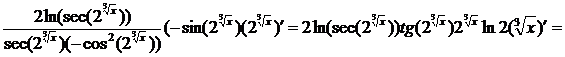

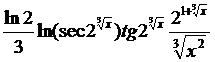 .◄
.◄
1)  (acos(tg(x))) 2)
(acos(tg(x))) 2)  (3sin(ctg(x))) 3)
(3sin(ctg(x))) 3)  (4tg(sin(x)))
(4tg(sin(x)))
4)  (3(tg(cos(x))) 5)
(3(tg(cos(x))) 5)  (7cos(3tg(4x))) 6)
(7cos(3tg(4x))) 6)  (6arctg(3cos(4x)))
(6arctg(3cos(4x)))
7)  (9cos(3arctg(6x))) 8)
(9cos(3arctg(6x))) 8)  (10ln(tg(3x))) 9)
(10ln(tg(3x))) 9)  (11ctg(3tg(7x)))
(11ctg(3tg(7x)))
10)  (6sin(tg(x))) 11)
(6sin(tg(x))) 11)  (4cosec(7tg(5x))) 12)
(4cosec(7tg(5x))) 12)  (55cos(arctg(x)))
(55cos(arctg(x)))
13)  (3(arcsin(x))) 14)
(3(arcsin(x))) 14)  (2cos(6arcctg(4x))) 15)
(2cos(6arcctg(4x))) 15)  (5sec(5tg(8x)))
(5sec(5tg(8x)))
16)  ln
ln  17)
17)  (ln(ln(ln(2x+1)))) 18)
(ln(ln(ln(2x+1)))) 18)  (sin(arcctg(sh3x)))
(sin(arcctg(sh3x)))
19)  (th(ctgx)) 20)
(th(ctgx)) 20)  (ln(arccosex)) 21)
(ln(arccosex)) 21)  (sin(shx))
(sin(shx))
22)  (sin(chx2)) 23)
(sin(chx2)) 23)  (log35(3thx)) 24)
(log35(3thx)) 24)  (cosec(th(arcsin7x)))
(cosec(th(arcsin7x)))
25) 
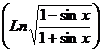 26)
26) 
 27)
27)  (sh(ch(e20x)))
(sh(ch(e20x)))
28)  (7ln(ln(x))) 29)
(7ln(ln(x))) 29)  (th(arctg(lnx))) 30)
(th(arctg(lnx))) 30)  (xxlnx)
(xxlnx)
Неявные функции
Пример 7.1. Уравнение x2 + y2 = 1 неявно определяет на интервале (-1,1) две функции:
y1(x) =  ,
,
y2(x) =  .
.
Найти их производные, не используя явных выражений.
►Пусть y(x) - любая из этих функций. Тогда, дифференцируя по x тождество
x2 + y2(x) = 1,
получим
2x + 2y(x)y`(x) = 0.
Отсюда
y`(x) = –x/y(x),
т. е.
y`1(x) = –x/y1(x) = –  , y`2(x) = –
, y`2(x) = – 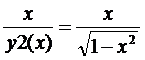 .◄
.◄
Пример 7.2. Уравнение arctg(y/x) = ln  задаёт неявную функцию. Найти ее производную.
задаёт неявную функцию. Найти ее производную.
► Продифференцировав равенство arctg(y/x) = ln 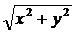 получим
получим
 ,
,
откуда
y` = 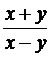 (x¹y).◄
(x¹y).◄
Найти производную неяной функции y = f(x), определяемой уравнением
1) sin(xy) + 2x = 3xy 2) cos(xy)+2x= 5xy
3) tg(xy) + 5x= 8xy 4) arccos(x2y) + log2x = 11xy
5) cos(xy4) + arcsin(23x3) = 22xy 6) sin(xy) + 2x = 3xy
7) x3 + y4 = xy 8) 5x7 + y8 = x8y8
9) 5x6 + y9 = xy9 10) 8x9 + y7 = x7y2
11) 4x6 + y3 = x5y2 12) log5(xy3) + arcsin(9x5) = 19xy
13) log8(xy8) + arcsin(4x7) = 18xy 14) log9(xy9) + arcsin(2x9) = 1995xy
15) log2(xy4) + arcsin(3x3) = 19xy 16) x2 + 2xy – y2 = 2x
17) y2 = 2px 18)  = 1
= 1
19)  20)
20) 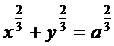
21) arctg 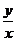 = ln
= ln 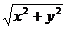 22) x3 – 2x2y2 + 5x + y – 5 = 0
22) x3 – 2x2y2 + 5x + y – 5 = 0
23) exy + xy = e 24) 2ylny = x
25) exsiny – eycosx = 0 26) sin(xy) + cos(xy) = 0
27) 2x+2y = 2x+y 28) x – y = arcsinx – arcsiny
29) xy = yx 30) 
Найти дифференциал функции
Пример 9.1. Найти дифференциал функции y = ctg3x
►Пользуясь тем, что dy = y`(x)dx найдем dy 
dy = – 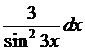 , x¹pk/3, kÎZ.◄
, x¹pk/3, kÎZ.◄
Пример 9.2. Найти дифференциал функции y=ln| 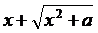 |
| 
► Используя определение дифференциала, находим
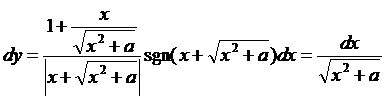 .◄
.◄
1) y = arccos(89log56(8x+4x9) ) 2) y = tg(exp(5x+x7))
3) y = cos(log3(2x+x4)) 4) y = tg(5log4(7x+x3))
5) y = arctg7log8(9x+x2)) 6) y = log3(5log4(7x)+6x8))
7) y = exp(6log7(16+2x5)) 8) y = arctg(9log9(14x+x5))
9) y = arcctg(8log12(13x)) 10) y = cos(exp(2x+x4))
11) y = arcsin(log3(6x+12(x7)3)) 12) y = (67log11(2x+33x77))
13) y = 45log12(x+2x12) 14)y = (34log9(11x+66x9))3
15) y = (23log3(7x+77x5))5 16) y = ln|x+  |
|
17) y = xex 18)y = tg(exp(16x+x9))
19) y = arctg(3log5(2x+4x3)) 20) y = arcctg(2log6(7x+2x4))
21) y = arcsin(ln(6x2)) 22) y = arccos 
23) y = arcsin  24) y = x2ln2x
24) y = x2ln2x
25) y =  26) y =
26) y = 
27) y = sinx – xcosx+4 28) y = x 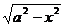 +
+  -5
-5
29) y = xlnx-x+1 30) y = xarcsinx+ 
Константу можно выносить за знак производной
Пример 1.1. y = 12sinx +17cosx + 99tgx
► Пользуясь правилом суммы и вынося константу за знак производной получаем
(12sinx + 17cosx + 99tgx)` = 12cosx – 17sinx +  ◄
◄
Пример 1.2. y = 11x101 +18 ln(x)
► y` = 1111x100 + 18/x◄
1)  ( 2sinx + 3cosx – 4xa+5 ax ) ( 2sinx + 3cosx – 4xa+5 ax ) | 2)  ( 3tgx + 3ctgx – 7ln(6x)+4 ax ) ( 3tgx + 3ctgx – 7ln(6x)+4 ax ) |
3)  ( 7arctgx + 5arcctg2x – 3log3(9x) ) ( 7arctgx + 5arcctg2x – 3log3(9x) ) | 4)  ( 6tgx + 3arcsinx – 7log5(7x) ) ( 6tgx + 3arcsinx – 7log5(7x) ) |
5)  ( 5tgx + 44arcsinx – 8log58(6x) ) ( 5tgx + 44arcsinx – 8log58(6x) ) | 6)  ( 32arctgx + 3ctgx – 4log6(6x) ) ( 32arctgx + 3ctgx – 4log6(6x) ) |
7)  ( 3sin2x + 5arcctgx – ln(6x) + 6x ) ( 3sin2x + 5arcctgx – ln(6x) + 6x ) | 8)  ( 23cosx + 78tgx – 99log3(6x)) ( 23cosx + 78tgx – 99log3(6x)) |
9)  (7secx + 5cosecx – 4og3(3x) + 7x ) (7secx + 5cosecx – 4og3(3x) + 7x ) | 10)  (7arcsinx + 9sinx – 3ln(x) + 2x ) (7arcsinx + 9sinx – 3ln(x) + 2x ) |
11)  ( 39cosx + 7arccosx –33 ax ) ( 39cosx + 7arccosx –33 ax ) | 12)  (4tgx + 45arcctgx – 87 ax ) (4tgx + 45arcctgx – 87 ax ) |
13)  ( 6arcsinx + 4ctgx – 6ln(x) + vx ) ( 6arcsinx + 4ctgx – 6ln(x) + vx ) | 14)  (5tgx + 2sinx – 56ln(6x) +x) (5tgx + 2sinx – 56ln(6x) +x) |
15)  ( 7arcctgx + cosx – 7ln(6x)+a 7x ) ( 7arcctgx + cosx – 7ln(6x)+a 7x ) | 16)  (1279x3 + 1279) (1279x3 + 1279) |
17)  (17chx + 34shx + 136th2x) (17chx + 34shx + 136th2x) | 18)  (28/4(sin(cos34x))) (28/4(sin(cos34x))) |
19)  (4xlnx + 88cos(lnx)) (4xlnx + 88cos(lnx)) | 20)  (24e3x + 3e21x) (24e3x + 3e21x) |
21)  (324x3 + 456x2 + 43x) (324x3 + 456x2 + 43x) | 22)  (77arccos(thx) + 99) (77arccos(thx) + 99) |
23)  (98tg3x + 84th5x) (98tg3x + 84th5x) | 24)  (354esinx + 945ecosx) (354esinx + 945ecosx) |
25)  (35cos(log3017x) + 92arctg5x) (35cos(log3017x) + 92arctg5x) | 26)  (73(2)3x + 198e45x) (73(2)3x + 198e45x) |
27)  (23earccos(x2) + (17e/2)arctgx) (23earccos(x2) + (17e/2)arctgx) | 28)  (73lnx3 + 3xlnx) (73lnx3 + 3xlnx) |
29)  (77th(arctgx)+356 (77th(arctgx)+356 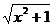 ) ) | 30)  (876ln (876ln 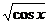 -126cos(79x)) -126cos(79x)) |
