Анализ факторных экспериментов
1. Полные факторные эксперименты и кодированные переменные. При проведении экспериментальных исследований часто применяются факторные эксперименты.
Пусть 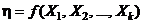 – функция отклика и задан план, матрица которого есть
– функция отклика и задан план, матрица которого есть 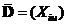 (i = 1, 2, ..., k; u = 1, 2, ..., N), где
(i = 1, 2, ..., k; u = 1, 2, ..., N), где 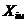 – значение переменной (фактора)
– значение переменной (фактора) 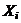 в u‑м опыте. Каждое из различных значений, принимаемых переменной
в u‑м опыте. Каждое из различных значений, принимаемых переменной 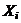 в эксперименте, называют уровнем этой переменной. Обозначим через si число различных уровней фактора Xi.
в эксперименте, называют уровнем этой переменной. Обозначим через si число различных уровней фактора Xi.
Определение 1. Эксперимент, в котором уровни каждого фактора комбинируются со всеми уровнями других факторов, называется полным факторным экспериментом.
Полный факторный эксперимент состоит из 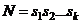 различных экспериментов, поэтому его называют экспериментом типа
различных экспериментов, поэтому его называют экспериментом типа 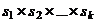 .
.
Определение 2.План называется симметричным, если все факторы имеют одинаковое число уровней, т. е. 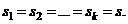 В этом случае полный факторный эксперимент принято называть экспериментом типа sk, где k – число факторов.
В этом случае полный факторный эксперимент принято называть экспериментом типа sk, где k – число факторов.
Предположим, что число различных значений, которые может принимать переменная 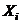 , в каждом опыте равно 2, т. е. s = 2. Тогда говорят, что переменная
, в каждом опыте равно 2, т. е. s = 2. Тогда говорят, что переменная 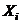 в каждом опыте варьируется на двух уровнях. Обозначим эти уровни через
в каждом опыте варьируется на двух уровнях. Обозначим эти уровни через 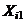 и
и 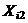 . Если
. Если 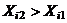 , то
, то 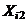 называют верхним уровнем, а
называют верхним уровнем, а 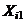 – нижним уровнем фактора
– нижним уровнем фактора 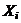 .
.
Обозначим 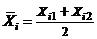 ,
, 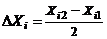 и введем новые переменные
и введем новые переменные
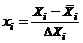 (i = 1, 2, ..., k).
(i = 1, 2, ..., k).
Переменные xi называют кодированными переменными. Легко проверить, что они могут принимать лишь два значения 1 (верхний уровень) и –1 (нижний уровень). Заменяя переменные 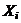 кодированными переменными
кодированными переменными 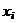 , можно представить функцию отклика в виде
, можно представить функцию отклика в виде
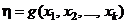 . (1)
. (1)
2. Полные факторные эксперименты типа 22 и 23. Если число независимых переменных равно двум, то равенство (1) приводится к виду 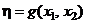 . Результаты наблюдений, отвечающих всевозможным комбинациям уровней переменных x1 и x2, сводятся в таблицу.
. Результаты наблюдений, отвечающих всевозможным комбинациям уровней переменных x1 и x2, сводятся в таблицу.
| Номер опыта | 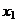 | 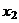 | 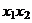 | Наблюдения |
| – 1 | – 1 | y1 | ||
| – 1 | – 1 | y2 | ||
| – 1 | – 1 | y3 | ||
| y4 |
Пусть функция отклика имеет вид
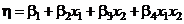
и в каждом варианте испытаний проводится по одному наблюдению. Тогда имеем полный факторный эксперимент типа 22. Матрица плана и матрица планирования:
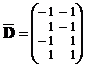 ,
, 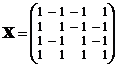 .
.
Столбцы матрицы X попарно ортогональны, следовательно, планирование является ортогональным. Отсюда, используя результаты п. 7 § 1, получаем, что МНК‑оценки параметров некоррелированны и имеют вид
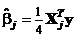 ,
,
где Xj – j-й столбец матрицы Х, при этом 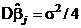 .
.
Пусть теперь число переменных равно трем и функция отклика имеет вид
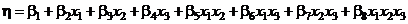 .
.
Рассмотрим все возможные комбинации уровней кодированных переменных 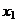 ,
, 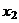 и
и 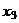 .
.
| Номер опыта | 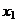 | 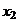 | 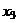 | 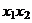 | 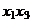 | 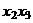 | 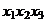 | Наблю- дения |
| – 1 | – 1 | – 1 | – 1 | y1 | ||||
| – 1 | – 1 | – 1 | – 1 | y2 | ||||
| – 1 | – 1 | – 1 | – 1 | y3 | ||||
| – 1 | – 1 | – 1 | – 1 | y4 | ||||
| – 1 | – 1 | – 1 | – 1 | y5 | ||||
| – 1 | – 1 | – 1 | – 1 | y6 | ||||
| – 1 | – 1 | – 1 | – 1 | y7 | ||||
| y8 |
Здесь, как легко убедиться, планирование является ортогональным. Поэтому МНК-оценки параметров bj некоррелированны и имеют вид
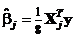 ,
,
при этом 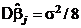 .
.
Пример 1. Полный двухфакторный эксперимент проводится на двух уровнях.
| Переменные | X1 | X2 |
| Нижний уровень | ||
| Верхний уровень |
Получены результаты исследований: 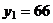 ,
, 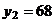 ,
, 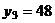 ,
, 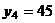 .
.
Для нахождения МНК-оценок 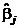 параметров
параметров 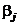 ортогонального плана пользуются расчетной таблицей.
ортогонального плана пользуются расчетной таблицей.
| i | 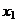 | 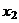 | 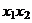 | 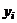 | 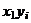 | 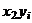 | 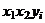 |
| – 1 | – 1 | – 66 | – 66 | ||||
| – 1 | – 1 | – 68 | – 68 | ||||
| – 1 | – 1 | – 48 | – 48 | ||||
С помощью расчетной таблицы получаем требуемые оценки:
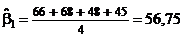 ;
; 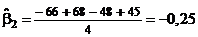 ;
;
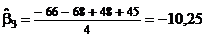 ;
; 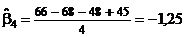 .
.
Значит, оценка функции отклика есть
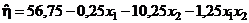 . (2)
. (2)
Возвращаясь к исходным переменным, имеем:
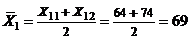 ,
, 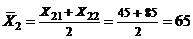 ,
, 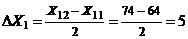 ,
, 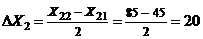 , значит,
, значит, 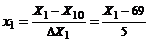 ,
, 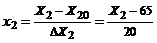 . Подставляя найденные выражения в (2), получаем
. Подставляя найденные выражения в (2), получаем
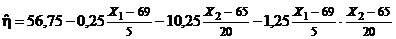 = =
= = 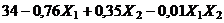 .
.
Пример 2. Полный трехфакторный эксперимент проводится на двух уровнях.
| Переменные | X1 | X2 | X3 |
| Нижний уровень | |||
| Верхний уровень |
Результаты исследований: 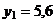 ;
; 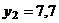 ;
; 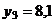 ;
; 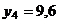 ;
; 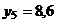 ;
; 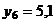 ;
; 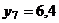 ;
; 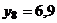 .
.
Составим расчетную таблицу для нахождения МНК‑оценок параметров 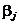 ортогонального плана.
ортогонального плана.
| i | ||||||||
| x1 | –1 | –1 | –1 | –1 | ||||
| x2 | –1 | –1 | –1 | –1 | ||||
| x3 | –1 | –1 | –1 | –1 | ||||
| x1x2 | –1 | –1 | –1 | –1 | ||||
| x1x3 | –1 | –1 | –1 | –1 | ||||
| x2x3 | –1 | –1 | –1 | –1 | ||||
| x1x2x3 | –1 | –1 | –1 | –1 | ||||
| yi | 5,6 | 7,7 | 8,1 | 9,6 | 8,6 | 5,1 | 6,4 | 6,9 |
| x1yi | –5,6 | 7,7 | –8,1 | 9,6 | –8,6 | 5,1 | –6,4 | 6,9 |
| x2yi | –5,6 | –7,7 | 8,1 | 9,6 | –8,6 | –5,1 | 6,4 | 6,9 |
| x3yi | –5,6 | –7,7 | –8,1 | –9,6 | 8,6 | 5,1 | 6,4 | 6,9 |
| x1x2yi | 5,6 | –7,7 | –8,1 | 9,6 | 8,6 | –5,1 | –6,4 | 6,9 |
| x1x3yi | 5,6 | –7,7 | 8,1 | –9,6 | –8,6 | 5,1 | –6,4 | 6,9 |
| x2x3yi | 5,6 | 7,7 | –8,1 | –9,6 | –8,6 | –5,1 | 6,4 | 6,9 |
| x1x2x3yi | –5,6 | 7,7 | 8,1 | –9,6 | 8,6 | –5,1 | –6,4 | 6,9 |
Используя расчетную таблицу, так же, как и в предыдущем примере, получаем требуемые оценки параметров: 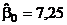 ;
; 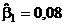 ;
; 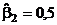 ;
; 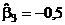 ;
; 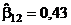 ;
; 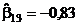 ;
; 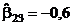 ;
; 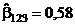 . Следовательно,
. Следовательно,
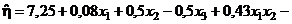
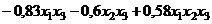 . (3)
. (3)
Возвращаемся к исходным переменным.
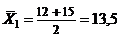 ;
; 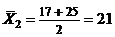 ;
; 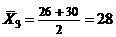 ;
; 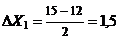 ;
; 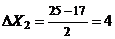 ;
; 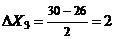 , значит,
, значит, 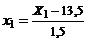 ,
, 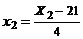 ,
, 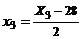 . Подставляя эти выражения в (3), получаем окончательно
. Подставляя эти выражения в (3), получаем окончательно
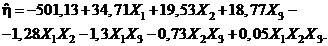
3. Факторные эксперименты с повторными наблюдениями. Пусть 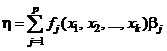 – функция отклика,
– функция отклика, 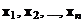 ; m, m, ..., m – спектр плана (число наблюдений в каждой точке xl одно и то же и равно m), mn = N. Пусть xl = (x1l, x2l, ..., xkl) и
; m, m, ..., m – спектр плана (число наблюдений в каждой точке xl одно и то же и равно m), mn = N. Пусть xl = (x1l, x2l, ..., xkl) и 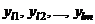 – повторные наблюдения в точке xl
– повторные наблюдения в точке xl 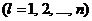 .
.
Матрицу плана 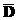 можно представить в виде матрицы из m блоков следующим образом:
можно представить в виде матрицы из m блоков следующим образом:
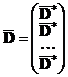 , где
, где 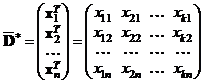 .
.
Таким образом, 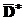 – матрица размеров
– матрица размеров 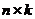 с различными строками,
с различными строками, 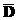 – матрица размеров
– матрица размеров 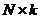 .
.
Определение. План называется полным факторным планом типа 2k с повторными наблюдениями кратности m, если матрица 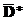 является матрицей полного факторного плана типа 2k.
является матрицей полного факторного плана типа 2k.
Пример. Пусть 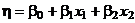 – функция отклика и задан план:
– функция отклика и задан план: 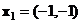 ,
, 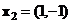 ,
, 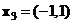 ,
, 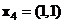 , причем в каждой точке число наблюдений m = 2. Тогда матрица плана записывается в виде:
, причем в каждой точке число наблюдений m = 2. Тогда матрица плана записывается в виде:
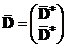 , где
, где 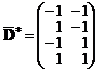 .
.
Так как 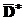 – матрица плана полного факторного эксперимента типа 22, то данный план является полным факторным планом с повторными наблюдениями кратности 2.
– матрица плана полного факторного эксперимента типа 22, то данный план является полным факторным планом с повторными наблюдениями кратности 2.
Матрица планирования имеет вид
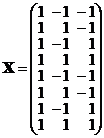
и является матрицей ортогонального планирования.
Если 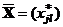 – матрица планирования, соответствующая функции отклика
– матрица планирования, соответствующая функции отклика 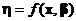 и матрице плана
и матрице плана 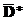 , то из ортогональности планирования для МНК-оценки вектора β имеем равенство
, то из ортогональности планирования для МНК-оценки вектора β имеем равенство 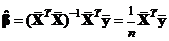 , в котором
, в котором 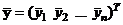 ,
, 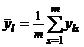 , а значит,
, а значит, 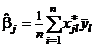 ( j = 0, 1, ..., p). В этом случае оценки
( j = 0, 1, ..., p). В этом случае оценки 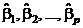 некоррелированны и имеют дисперсию
некоррелированны и имеют дисперсию 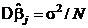 .
.
4. Насыщенное и ненасыщенное планирование.
Определение 1. Пусть матрица планирования X имеет ранг, равный числу p неизвестных параметров в функции отклика. Факторный план называется насыщенным, если p = N, и ненасыщенным, если p < N.
Ненасыщенность плана полного факторного эксперимента означает, что имеется избыточность 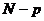 опытов, необходимых для нахождения МНК-оценок параметров
опытов, необходимых для нахождения МНК-оценок параметров 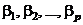 в функции
в функции 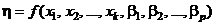 .
.
Пример 1. Пусть 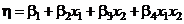 и планируется полный факторный эксперимент типа 22. Тогда планирование будет насыщенным, т. к. ранг матрицы планирования Xравен 4 и при этом число наблюдений N и число неизвестных параметров p также равны 4.
и планируется полный факторный эксперимент типа 22. Тогда планирование будет насыщенным, т. к. ранг матрицы планирования Xравен 4 и при этом число наблюдений N и число неизвестных параметров p также равны 4.
Пример 2. Если 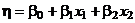 и имеется полный факторный эксперимент типа 22, то планирование будет ненасыщенным, т. к. ранг матрицы планирования
и имеется полный факторный эксперимент типа 22, то планирование будет ненасыщенным, т. к. ранг матрицы планирования

равен 3, а 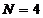 .
.
Определение 2. Пусть n – число точек спектра факторного плана с повторными наблюдениями кратности m (N = mn) и r – ранг матрицы планирования X. Тогда план называется насыщенным, если 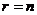 , и ненасыщенным, если
, и ненасыщенным, если 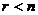 .
.
5. Проверка гипотезы адекватности. Рассмотрим факторный эксперимент с кратными повторными наблюдениями yls (l = 1, 2, ..., n; s = 1, 2, ..., m). Проверим гипотезу H0 адекватности модели
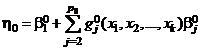 , (4)
, (4)
где 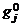 – известные функции, задаваемые равенствами вида
– известные функции, задаваемые равенствами вида 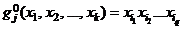 (1 m i1 < i2 < ... < iq m k), а
(1 m i1 < i2 < ... < iq m k), а 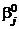 – неизвестные параметры. Функции отклика (4) и матрице
– неизвестные параметры. Функции отклика (4) и матрице 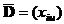 (i = 1, 2, ..., k; u = 1, 2, ..., N; N = mn) полного факторного плана соответствует матрица планирования
(i = 1, 2, ..., k; u = 1, 2, ..., N; N = mn) полного факторного плана соответствует матрица планирования 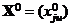 ( j = 1, 2, ..., p0; u = 1, 2, ..., N). Столбцы матрицы X0 должны удовлетворять условиям:
( j = 1, 2, ..., p0; u = 1, 2, ..., N). Столбцы матрицы X0 должны удовлетворять условиям:
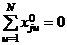 ( j = 2, 3, …, p); (5)
( j = 2, 3, …, p); (5)
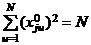 ( j = 1, 2, …, p); (6)
( j = 1, 2, …, p); (6)
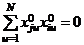
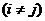 . (7)
. (7)
Будем предполагать, что наблюдения yls являются нормальными и некоррелированными, причем 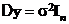 , где
, где 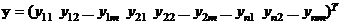 – вектор-столбец наблюдений;
– вектор-столбец наблюдений; 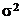 – неизвестный параметр.
– неизвестный параметр.
Гипотеза 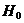 состоит в том, что My = X0β0, где
состоит в том, что My = X0β0, где 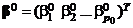 . Эта гипотеза проверяется при альтернативной гипотезе
. Эта гипотеза проверяется при альтернативной гипотезе 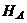 : My ¹ X0β0.
: My ¹ X0β0.
Для проверки гипотезы 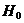 нужно вычислить отношение
нужно вычислить отношение 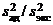 . Величина
. Величина 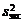 представляет собой несмещенную оценку для
представляет собой несмещенную оценку для 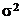 . Полагая в формуле (6) § 2 m1 = m2 = ... = mi = m, получаем
. Полагая в формуле (6) § 2 m1 = m2 = ... = mi = m, получаем
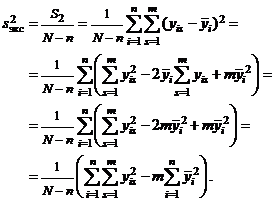 .
.
Таким образом,
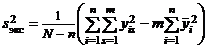 . (8)
. (8)
Оценка (5) § 2 дисперсии 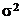 , связанная с неадекватностью модели, есть
, связанная с неадекватностью модели, есть 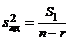 , где r – ранг матрицы X0.
, где r – ранг матрицы X0.
Пусть r = 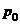 , тогда, учитывая (5) – (7), получаем
, тогда, учитывая (5) – (7), получаем
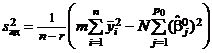 , (9)
, (9)
где 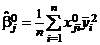 , j = 1, 2, ..., p0.
, j = 1, 2, ..., p0.
Далее вычисляем 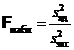 и по таблице распределения Фишера по уровню значимости a и степеням свободы n – r и N – n находим
и по таблице распределения Фишера по уровню значимости a и степеням свободы n – r и N – n находим 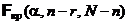 .
.
Если 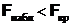 , то гипотеза H0 принимается.
, то гипотеза H0 принимается.
Если 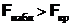 , то гипотеза H0 отклоняется.
, то гипотеза H0 отклоняется.
Пример. Предположим, что зависимость прочности бетона R от двух факторов – расхода цемента X1 и расхода воды X2 – имеет вид: 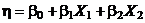 . Полный двухфакторный эксперимент проводится на двух уровнях:
. Полный двухфакторный эксперимент проводится на двух уровнях:
| Уровень | Расход цемента X1 | Расход воды X2 |
| Нижний | ||
| Верхний |
Результаты исследований представлены таблицей.
| i | 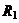 | 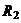 | 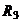 | 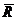 |
| 28,6 | 31,1 | 29,5 | 29,7 | |
| 44,3 | 47,8 | 46,2 | 46,1 | |
| 22,9 | 24,6 | 21,9 | 23,1 | |
| 38,7 | 38,7 | 35,3 | 36,7 |
МНК-оценки 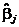 параметров
параметров 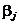 ортогонального планирования находятся так же, как в примере 1 п. 3:
ортогонального планирования находятся так же, как в примере 1 п. 3: 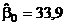 ;
; 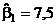 ;
; 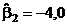 , отсюда оценка функции отклика –
, отсюда оценка функции отклика – 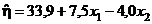 , или, переходя к исходным переменным,
, или, переходя к исходным переменным, 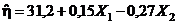 .
.
Проверим, является ли полученная модель адекватной. Имеем N = 12, n = 4, m = 3, r = 3. По формулам (8) и (9)
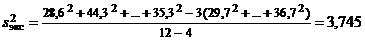 ,
,
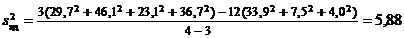 .
.
Следовательно, 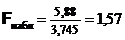 . Далее по таблице критических точек распределения Фишера по уровню значимости a = 0,05 и степеням свободы n – r = 1 и N – n = 8 находим
. Далее по таблице критических точек распределения Фишера по уровню значимости a = 0,05 и степеням свободы n – r = 1 и N – n = 8 находим 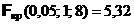 . Так как
. Так как 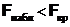 , то гипотеза, утверждающая, что модель
, то гипотеза, утверждающая, что модель 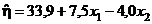 адекватна, принимается.
адекватна, принимается.
§ 4. Оптимизация планов. Поиск экстремума функции отклика
1. Построение линейных оптимальных планов. Пусть функция отклика является полиномом первой степени от k переменных:
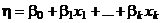 . (1)
. (1)
Определение 1. План называется линейным, если ему соответствует функция отклика (1) и он позволяет получить несмещенные МНК-оценки параметров 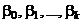 .
.
Если матрица линейного плана есть
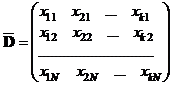 , (2)
, (2)
то матрица планирования для этого плана имеет вид
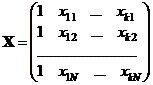 .
.
Определение 2. Линейный план называется линейным ортогональным планом, если столбцы матрицы Xпопарно ортогональны, т. е.
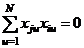
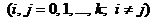 . (3)
. (3)
Линейные планы широко используются в экспериментальных исследованиях, где эффекты взаимодействий факторов незначимы или вообще отсутствуют. Они используются также в задачах поиска экстремума функции отклика.
Пусть матрица планирования X имеет ранг k + 1 и вектор наблюдений 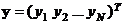 удовлетворяет условиям
удовлетворяет условиям 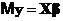 ;
; 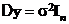 , тогда для ковариационной матрицы МНК-оценок
, тогда для ковариационной матрицы МНК-оценок 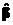 вектора β имеем равенство
вектора β имеем равенство
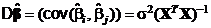 .
.
Будем предполагать, что
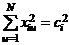 ,
, 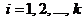 , (4)
, (4)
где величины ci заданы; положим также 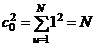 .
.
Требуется выбрать матрицу планирования Xили матрицу линейного плана 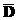 , так чтобы дисперсии
, так чтобы дисперсии 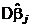 МНК-оценок параметров
МНК-оценок параметров 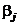
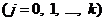 в классе линейных планов с ограничениями (4) были минимальными.
в классе линейных планов с ограничениями (4) были минимальными.
План, минимизирующий дисперсии оценок параметров, называют линейным оптимальным планом. Задача построения таких планов решается с помощью теоремы Бокса, которую мы приведем без доказательства.
Теорема Бокса. Пусть функция отклика имеет вид (1), столбцы матрицы 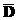 линейного плана удовлетворяют условиям (4) и ранг матрицы X равен k + 1. Тогда для МНК-оценок параметров
линейного плана удовлетворяют условиям (4) и ранг матрицы X равен k + 1. Тогда для МНК-оценок параметров 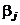 выполняется неравенство
выполняется неравенство
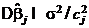 (
( 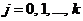 ), (5)
), (5)
причем минимум дисперсий 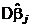 в классе линейных планов с ограничениями (4) достигается тогда и только тогда, когда столбцы матрицы Xпопарно ортогональны.
в классе линейных планов с ограничениями (4) достигается тогда и только тогда, когда столбцы матрицы Xпопарно ортогональны.
В частности, поскольку первый столбец матрицы X состоит из единиц (x0u = 1), из условия ортогональности (3) при j = 0 следует 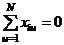 . Таким образом, получаем
. Таким образом, получаем
Следствие. Необходимым условием минимума дисперсий МНК-оценок 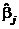 является выполнение при всех i = 1, 2, ..., k равенства
является выполнение при всех i = 1, 2, ..., k равенства 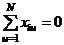 (условие симметрии плана).
(условие симметрии плана).
2. Градиентный метод. Будем предполагать, что функция отклика 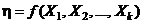 непрерывна и имеет непрерывные частные производные 1-го порядка в ограниченной замкнутой области G Í Ñk.
непрерывна и имеет непрерывные частные производные 1-го порядка в ограниченной замкнутой области G Í Ñk.
Определение 1. Функция f называется унимодальной в области G, если она в этой области имеет единственный экстремум.
Пусть изменение функции многих переменных вдоль некоторой траектории, проведенной из точки 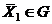 в точку
в точку 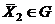 и определенной в области G, задается уравнением
и определенной в области G, задается уравнением 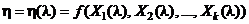 , где l – параметр, пробегающий числовой отрезок [0; 1].
, где l – параметр, пробегающий числовой отрезок [0; 1].
Траекторию назовем строго возрастающей (строго убывающей), если функция h(l) строго возрастает (строго убывает) на отрезке [0; 1].
Определение 2. Пусть 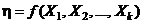 – функция отклика, определенная в области G и имеющая во внутренней точке
– функция отклика, определенная в области G и имеющая во внутренней точке 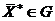 максимум или минимум. Функция называется строго унимодальной, если отрезок, проведенный из любой точки
максимум или минимум. Функция называется строго унимодальной, если отрезок, проведенный из любой точки 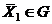 в точку
в точку 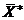 , является строго возрастающей траекторией в случае максимума или строго убывающей траекторией в случае минимума.
, является строго возрастающей траекторией в случае максимума или строго убывающей траекторией в случае минимума.
Экстремум функции 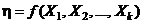 отыскивается методом спуска (или подъема) по исследуемой поверхности. Этот метод основан на построении последовательности точек
отыскивается методом спуска (или подъема) по исследуемой поверхности. Этот метод основан на построении последовательности точек 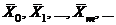 , лежащих в области G и таких, что
, лежащих в области G и таких, что 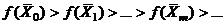 (метод спуска) или
(метод спуска) или 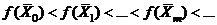 (метод подъема).
(метод подъема).
Наиболее часто применяемая в практике исследований разновидность метода спуска и подъема – так называемый градиентный метод, при котором последовательность точек 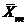 определяется с помощью равенства
определяется с помощью равенства
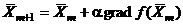 , (6)
, (6)
где 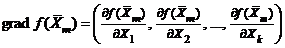 – градиент функции f в точке
– градиент функции f в точке 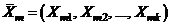 ; a – некоторое положительное число. В этом случае функция f предполагается строго унимодальной.
; a – некоторое положительное число. В этом случае функция f предполагается строго унимодальной.
Различные варианты градиентного метода отличаются друг от друга способом выбора a. Одним из вариантов градиентного метода является метод наискорейшего спуска (или подъема). При оптимизации технологических процессов в теории планированияэксперимента используется его статистический аналог – метод Бокса и Уилсона. В этом методе используется не сам градиент, а его оценка.
3. Оценивание градиента.Пусть функция отклика
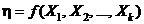 (7)
(7)
определена в области G Ì Ñk.
Выберем произвольно точку 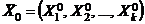
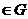 . Используя эту точку, построим полный факторный эксперимент. Выберем для каждого i = 1, 2, ..., k нижний уровень
. Используя эту точку, построим полный факторный эксперимент. Выберем для каждого i = 1, 2, ..., k нижний уровень 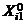 и верхний уровень
и верхний уровень 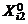 так, чтобы было
так, чтобы было 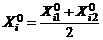 . Положим
. Положим 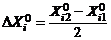 , введем кодированные переменные
, введем кодированные переменные 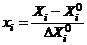 и выразим функцию отклика (7) через кодированные переменные:
и выразим функцию отклика (7) через кодированные переменные:
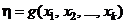 . (8)
. (8)
Под задачей оценивания градиента будем понимать определение оценки градиента функции отклика (8) в точке x0 = (0, 0, ..., 0). Предположим, что в окрестности точки x0 функция (8) допускает разложение по формуле Маклорена:
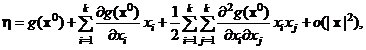 (9)
(9)
где 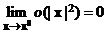 . Введем обозначения:
. Введем обозначения: 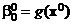 ,
, 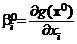 ,
, 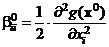 ,
, 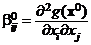 . Тогда равенство (9) перепишется в виде
. Тогда равенство (9) перепишется в виде
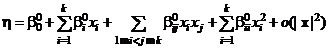 .
.
Так как 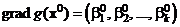 , задача оценивания градиента сводится к нахождению МНК-оценок параметров
, задача оценивания градиента сводится к нахождению МНК-оценок параметров 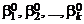 .
.
Пусть матрица полного факторного плана с центром в точке 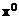 задана равенством (2).
задана равенством (2).
Для простоты будем считать, что в замкнутой области 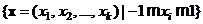 функция отклика достаточно точно аппроксимируется линейной функцией, т. е.
функция отклика достаточно точно аппроксимируется линейной функцией, т. е.
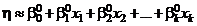 . (10)
. (10)
Тогда матрице плана 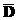 и функции отклика (10) соответствует матрица планирования
и функции отклика (10) соответствует матрица планирования 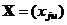 ( j = 0, 1, 2, ..., k; u = 1, 2, ..., N; x0u = 1) и для МНК-оценки параметра
( j = 0, 1, 2, ..., k; u = 1, 2, ..., N; x0u = 1) и для МНК-оценки параметра 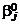 имеем равенство
имеем равенство
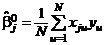 ( j = 0, 1, 2, ..., k),
( j = 0, 1, 2, ..., k),
где 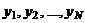 – наблюдения в точках плана.
– наблюдения в точках плана.
Поскольку 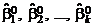 являются оценками компонент градиента
являются оценками компонент градиента 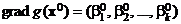 , т. е. частных производных
, т. е. частных производных 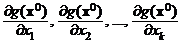 , то МНК-оценка градиента функции отклика в точке
, то МНК-оценка градиента функции отклика в точке 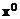 определяется равенством
определяется равенством
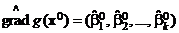 .
.
Пример. Пусть h = f (x1, x2) – функция отклика (x1, x2 –кодированные переменные), матрица плана и результаты наблюдений 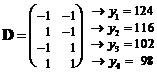 . Используя аппроксимацию вида h » b0 + b1x1 + b2x2 + b3x1x2 (
. Используя аппроксимацию вида h » b0 + b1x1 + b2x2 + b3x1x2 ( 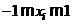 ), найдем оценку градиента в центре плана (0, 0). Так как
), найдем оценку градиента в центре плана (0, 0). Так как 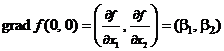 и
и 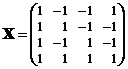 , то планирование ортогонально,
, то планирование ортогонально, 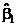 = (–y1 + y2 – y3 + y4) : 4 = –3,
= (–y1 + y2 – y3 + y4) : 4 = –3, 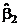 = (–y1 – y2 + y3 + y4) : 4 = –10 и, следовательно, получаем
= (–y1 – y2 + y3 + y4) : 4 = –10 и, следовательно, получаем 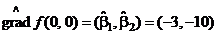 .
.
4. Метод Бокса и Уилсона. Будем предполагать, что функция отклика (7) в области G строго унимодальна. Поиск ее максимума может быть осуществлен методом, предложенным Боксом и Уилсоном.
Пусть 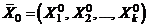 – начальная точка поиска максимума. При переходе к кодированным переменным точке
– начальная точка поиска максимума. При переходе к кодированным переменным точке 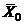 соответствует точка
соответствует точка 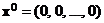 , а функция отклика (7) принимает вид (8).
, а функция отклика (7) принимает вид (8). 
Пусть 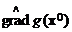 – оценка градиента в точке
– оценка градиента в точке 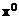 , полученная с использованием факторного эксперимента, матрица плана которого
, полученная с использованием факторного эксперимента, матрица плана которого 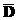 задана равенством (2). Для поиска максимума сделаем некоторый шаг из точки
задана равенством (2). Для поиска максимума сделаем некоторый шаг из точки 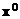 в направлении оценки градиента
в направлении оценки градиента 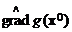 . Положим
. Положим
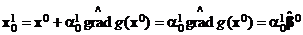 , (11)
, (11)
где параметр 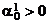 ,
, 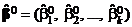 – МНК-оценка градиента,
– МНК-оценка градиента, 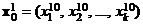 ,
, 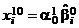 (i = 1, 2, ..., k).
(i = 1, 2, ..., k).
Точке 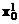 в системе координат кодированных переменных соответствует точка
в системе координат кодированных переменных соответствует точка 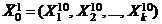 в системе координат исходных переменных, при этом имеем
в системе координат исходных переменных, при этом имеем 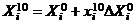 .
.
Выполним в точке 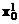 наблюдения
наблюдения 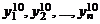 и найдем в ней оценку функции отклика
и найдем в ней оценку функции отклика
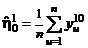 . (12)
. (12)
Так как измерение функции отклика происходит с ошибкой, то в точке 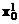 можно найти только ее оценку, а не точное значение. Предположим, что оценка
можно найти только ее оценку, а не точное значение. Предположим, что оценка 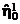 значимо больше оценки
значимо больше оценки 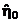 функции отклика в точке
функции отклика в точке 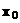 , где согласно (10)
, где согласно (10) 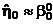 .
.
В этом случае делаем второй шаг в направлении оценки градиента 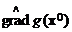 и т. д. В общем виде, учитывая (11), для l-го шага имеем:
и т. д. В общем виде, учитывая (11), для l-го шага имеем:
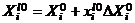 ,
, 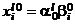 (i = 1, 2, ..., k), (13)
(i = 1, 2, ..., k), (13)
где
