Вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Если вектор а не параллелен вектору b, то a и b линейно независимы
Максимальное количество линейно независимых векторов на плоскости = 2.
Вывод:
Любые два вектора принадлежащие V2 и не параллельные, образуют базис на плоскости.
Декартов базис
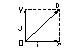
i; j – орты
Теорема: Разложение вектора по базису единственно.
Доказательство: (от противного)
Билет 7
Скалярное произведение векторов, проекция одного вектора на другой, критерий ортогональности векторов.
Скалярное произведение называется число, равное произведению модулей этих векторов на косинус угла между ними.
Обозначение:
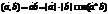
Свойства векторного произведения:
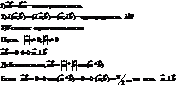
Проекция одного вектора на другой:
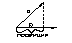

Скалярное произведение векторов в декартовой системе координат:
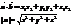
Билет 10
Различные уравнения плоскости в пространстве, угол между плоскостями, расстояние от точки до плоскости.
Угол между плоскостями –угол между их нормалями.

Уравнения плоскости в пространстве:

Рисунок
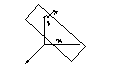

Билет 9
Смешанное произведение, его геометрический смысл, критерий компланарности векторов.
Смешанное произведение 3-х векторов:
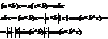
Условие комплонарности:
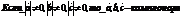
Доказательство:

Свойства смешанного произведения:
1)Если abc>0 , то тройка векторов правая
Если abc<0 , то тройка векторов левая
2) abc=bca=cab
-bac=abc=-cba=-acb
3)(λa)bc=λ(abc)
4)(a1+a2)bc=a1bc+a2bc
Площадь параллелепипеда = |abc|
Площадь пирамиды = 1/6 |abc|
В прямоугольной декартовой системе координат:
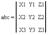
Геометрический смысл:
Модуль смешанного произведения abc равен объему параллелепипеда, построенного на векторах a,b,c а знак отвечает за ориентацию тройки .
Билет 11
Различные уравнения прямой в пространстве, переход от общего уравнения к каноническому, расстояние от точки до прямой.
Линии в пространстве могут быть заданы 2-я способами:
1)Линия – пересечение 2-х поверхностей:

2)Линия - траектория движущейся точки:
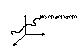
x=x(t)
y=y(t) t-параметр
z=z(t)
а)
Условие 1:
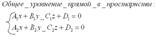
Для первого уравнения δ1 и для второго δ2

Сумма уравнений 1 представляет общее уравнение прямой в V3 тогда и только тогда, когда выполняется условие 2
б)
Канонические уравнения прямой:

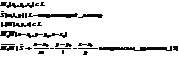
Замечание:
Если в формуле (2) какой-либо знаменатель = 0, то и соответственно числитель тоже нужно прировнять к нулю.
в)
Уравнения прямых проходящих через 2-е точки:

Расстояние от точки до прямой:


Билет 12
Различные уравнения прямой на плоскости, геометрический смысл параметров.
Уравнения:

Геометрический смысл параметров:
Билет 13
Угол между двумя прямыми, условия параллельности и перпендикулярности, расстояние от точки до прямой(на плоскости и в пространстве).
Угол между 2-я прямыми - угол, между их направляющими векторами
Условия || и перпендикулярности 2-х прямых решаются из условий || и перпендикулярности соответственных векторов n и S:

Расстояние от точки до прямой!
В пространстве:


На плоскости:

Билет 14
Эллипс.
Эллипс – множество точек плоскости, сумма расстояний, которых до 2-х заданных точек (фокусов) есть величина постоянная, равная 2 а.
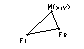
Введем ДПСК
Так, что ось Ох совпадает с фокальной осью F1F2, ось Оу – через середину F1F2.
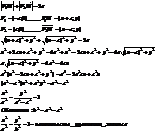
a>c
a,b-полуоси эллипса
Та ось, на которой находятся фокусы, называется большой
В доказанном случае а-большая
b-малая
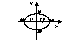
A1A2-большая ось
B1B2-малая ось
|A1A2|=2a
|B1B2|=2b
|F1F2|=2c
a^2=b^2+c^2
Если F1=F2(c=0), то эллипс является окружностью.
Билет 15
Гипербола.
Гипербола – это множество точек плоскости, модуль разности расстояния, которых до 2-х заданных точек (фокусов) есть величина постоянная, равная 2а.
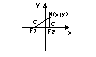
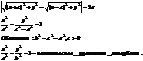
Гипербола имеет две асимптоты
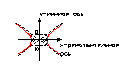
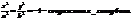
Если угол между асимптотами = п/2 , то это равносторонняя гипербола.
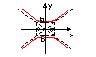
Если при этом асимптоты принять за оси ПДСК, то получим гиперболу показанную ниже:
y=c/x
Эксцентриситет
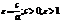
Чем меньше эксцентриситет, тем больше вытянут вспомогательный прямоугольник вдоль фронтальной оси.
Билет 16
Парабола.
Парабола – множество точек плоскости, равноудаленных от дальней точки (фокуса) и данной прямой (директриса)
Выберем ПДСК
Проведем Ох перпендикулярно директрисе, через фокус F.
Оу через середину расстояния между F и директрисой.
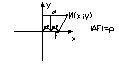
По определению p=d
|KM|=|FM|
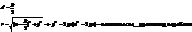
Билет 19
