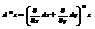Частные производные высших порядков.

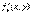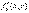Если функция f(x, y) определена в некоторой области D, то ее частные производные и тоже будут определены в той же области или ее части

Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второго порядка.

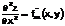
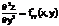
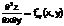
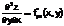
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение. Частные производные вида

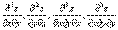
и т.д. называются смешанными производными.

Теорема. Если функция f (x,y) и ее частные производные 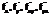определены и непрерывны в точке М(х,у) и ее окрестности, то верно соотношение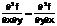

Т.е. частные производные высших порядков не зависят от порядка дифференцирования. Аналогично определяются дифференциалы высших порядков.

23 Частные дифференциалы. Полное приращение и полный дифференциал.

Рассмотрим функцию z = f(x;y), которая непрерывна в области D и имеет непрерывные частные производные

Рассмотрим полное приращение функции Δ z=f(x+ Δ x;y+ Δy)-f(x;y).

Требуется выразить его через частные производные функции и приращения ее аргументов. Прибавим и отнимем в правой части полного приращения выражение f(x;y+ Δy) и сгруппируем в виде Δ z=[f(x+ Δ x;y+ Δy)-f(x;y+ Δy)]+[f(x+ Δ x;y+ Δy)-f(x;y)].ко второй разности применим теорему Лагранжа как к функции одной переменной у, так как х считается постоянной величиной.Также для первой разности считая функцию от х, применим ту же теорему. И так как по условию частные производные непрерыны, то существуют и их пределы.

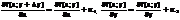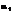Тогда из основной теоремы о пределе и бесконечно малой имеем где и 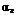бесконечно малые более высокого порядка, чем Δ x и Δ y.Тогда полное приращение равно:

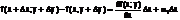
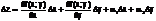Полное приращение оказалось линейным относительно Δ x и Δy

Определение. Главная часть полного приращения функции называется полным дифференциалом и обозначается:

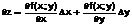
Если существует полный дифференциал, то функция дифференцируемая. Так как бесконечно малые 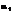и 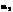стремятся к нулю, то полное приращение приближенно равно полному дифференциалу 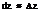В связи с тем, что х,у независимые переменные, приращения Δ x,Δ у можно принять за дифференциалы функции dx,dy. Тогда окончательно получим 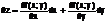(1) Предположим что дана функция n переменных u = f (x;y;z;…..;t), тогда аналогично формуле (1) ее полный дифф-л выражается формулой (*):

(*)

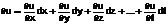Полный дифф-л функции нескольких переменных равен сумме частных производных, умноженных на дифф-лы соответствующих переменных.

24 Дифференциалы высших порядков. Инвариантность формы полного дифференциала.

Рассмотрим полный дифференциал функции двух переменных

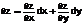Определение. Полный дифференциал дифференциала первого порядка называется дифференциалом второго порядка: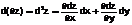

Используя формулу полного дифф-ла и дифференцируя как произведения, получим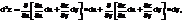

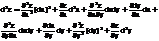
Итак,(*) 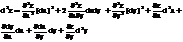Если переменные х,у независимые, то в выражении (*) последние четыре члена обратятся в ноль, так как производные и дифф-лы от dx, от dy равны нулю. Но если функция z сложная, то х;у зависят от других независимых переменных, то для дифф-ла второго порядка используется формула (*). Мы же будем в дальнейшем рассматривать функцию двух переменных, где х,у независимые. Поэтому дифф-л второго порядка представляется в виде.

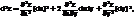Найдем третий дифф-л

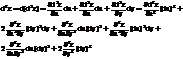
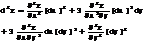Перепишем дифф-л третьего порядка в виде

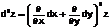
Здесь под степенью при раскрытии скобки подразумевается порядок производной и под произведением различных степеней подразумевается смешанная производная различных порядков функции. Дифф-лы высших порядков для функции двух независимых переменных символически напоминают бином. Таким образом, по аналогии