Линейная регрессия от одного фактора

Уравнение линии регрессии на плоскости в декартовых координатах имеет вид выражения (4.5).

Задачу метода наименьших квадратов аналитически можно выразить следующим образом:

П ~

Ф(Ьо,Ь^)= X[y i ^-(b() + bjxj)] —> min . (4-13)

i=l^0,bj

Для решения этой задачи, как известно из математического анализа, не­обходимо вычислить частные производные функции Ф по коэффициентам b₀, bi и приравнять их нулю:

<90(bn,bi) <90(bn,bi)

--------- —— = 0;---------- —— = 0. (4.14)

Система нормальных уравнений (4.8) в этом случае примет вид

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

П ft ft

2_j[y_f —(b_Q +b_xx_t)\ = 0; nb₀ + b_} / x. = /_ly_i,

f-i

F-i

^{n n n n}

¹^[y_i-(b_Q-\-b_lx_i)]-x_i = 0; b₀ ^jc_f+Z>₁ ^jc? =^х_{у_г

f-i

f-i

f-i

. '-1

(4.15)

Решение этой системы относительно bo и bi дает

bg

п п ₉ п п

Zyi Z(xi) ~Z(xiyi)Zxi

i=l

i=l

Л2 n ] Zx i U=i J

i=l i=l

n ^

n Yj (xi) i=l

(4.16)

n

n

"l

n

n n

n Zx i y i ~ Zx i Zy i Z(x i ^_x)(y i ~ y)

i=l

i=l

i=l i=l

Л2 n | Zx i

n

11 r>

n X (xi) i=l

Z(xi ^_x) i=l

(4.16a)

т.е. для

расчета b₀ и bi необходимо определить Zx i>ZybZx i ybZ(x i)²-

Коэффициент bo (свободный член уравнения регрессии) геометрически представляет собой расстояние от начала координат до точки пересечения ли­нии регрессии с осью ординат, а коэффициент bi характеризует тангенс угла наклона линии регрессии к оси ОХ.

Если же определяют уравнение регрессии в виде у = Ьо +Ь]х + Ъцх , то система уравнений для нахождения bo, bi, Ьц будет иметь следующий вид:

/\у. =b_Qn + b_l2^x_i +b_u/_txf

i-\

i-\

i-\

tx.y.=botx.⁺bitx*⁺butx

l-\ П

f-ii-\i-\

n n n n

cf+b^+b^t

f-ii-\i-\

l-\

(4.166)

Из уравнений (4.15) и (4.166) вытекает правило записи любых систем нормальных уравнений: необходимо записать столько уравнений в системе,

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

сколько неизвестных коэффициентов содержится в искомом уравнении, всякий раз суммируя произведения членов исходного уравнения на переменную при искомом коэффициенте.

Оценку силы линейной связи осуществляют по выборочному (эмпириче­скому) коэффициенту парной корреляции г_ху. Выборочный коэффициент корре­ляции может быть вычислен двумя способами.

1. Как частный случай корреляционного отношения для линейного урав­
нения регрессии.

С учетом того, что у = Ь₀+Ь₁х,

о*2 1 Дп

Z[bo + bix i -bg -bjx] =b₁S x , (4-17)

величина отношения S y/S y будет равна

r xy = bjS x /S y , (4.18)

где S_x и S_y - выборочные средние квадратичные отклонения.

2. Как среднее значение произведения центрированных случайных вели­
чин, отнесенное к произведению их среднеквадратичных отклонений:

П п

Z(xi ~x)(yi ~ У) Z(xi ~x)(yi ~ У)

i=l_____________i=l________________ _________________ л(\\

(n-l)S x S y

г_Ху =---------------------------------- = —j =. (4. I У]

n „n

Z(xi_x) Z(yi~y) i=l i=l

\

Покажем, что две последние формулы эквивалентны. Для этого преобра­зуем выражение (4.19) к виду

п

Z(xi -х)(у{ -у) = r_Xy(n-l)SxSy. i=l

Подставляя последнее выражение в формулу (4.16а), имеем

г (n-l)SxS hS ------------------- !? V (Х; - Х)1 У

г (п- 1)5* S
^ъ\=---------------- = rxyS_y/S_x, откуда г^

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

Как правило, по результатам экспериментов находят S_x, S_y, х,у и рас­считывают г_ху по формуле (4.19), а затем, используя эти величины, определяют коэффициенты уравнения регрессии:

bi=r_Xy S y /S x ; bo=y-bix. (4.20)

Коэффициент корреляции г_ху изменяется в пределах -1< г_ху <+1.

Положительная корреляция между случайными величинами характери­зует такую стохастическую зависимость между величинами, когда с возраста­нием одной из них другая в среднем также будет возрастать. При отрицатель­ной корреляции с возрастанием одной случайной величины другая в среднем будет уменьшаться. Чем ближе значение г_ху к единице, тем теснее статистиче­ская связь.

Отметим еще раз область применимости выборочного коэффициента корреляции для оценки тесноты связи.

1. Коэффициент парной корреляции значений у и х применительно к од-нофакторной зависимости характеризует тесноту группирования дан­ных лишь относительно прямой (например, линия А на рис. 4.8, а). При более сложной зависимости (рис.4.8, б) коэффициент корреляции г_ху будет оценивать тесноту экспериментальных точек относительно некоторой прямой, обозначенной буквой А, что, естественно, несет мало сведений о тесноте их группирования относительно искомой кривой у - f(x).

2. Коэффициент парной выборочной корреляции имеет четкий физиче­ский смысл только в случае двумерного нормального распределения параметров, т.е. когда для каждого значения X, например х-i, х₂, х₃, существует совокупность нормального распределения у и наоборот, а дисперсия зависимой переменной при изменении значения аргумента остается постоянной (рис. 4.9).

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

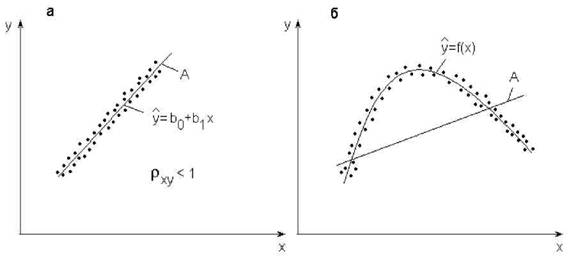
Рис.4.8. К понятию коэффициента парной корреляции

Даже при выполнении этих, вообще говоря достаточно жестких условий, не всякое значение выборочного коэффициента корреляции является доста­точным для статистического обоснования выводов о наличии действительно надежной корреляционной связи между фактором и откликом. Надежность ста­тистических характеристик ослабевает с уменьшением объема выборки (п). Так, при п=2 через две экспериментальные точки можно провести только одну прямую и зависимость будет функциональной, при этом выборочный коэффи­циент корреляции равен единице (г_ху=1). Однако это не означает надежность полученных статистических характеристик в силу весьма и весьма ог­раниченного объема выборки. Значит, вычислять коэффициент корреляции по результатам двух наблюдений бессмысленно, так как он заведомо будет равен единице, и это будет обусловлено не свойствами переменных и их взаимным отношением, а только числом наблюдений.

гху от его действительно­го значения гху*. При дос­таточно большом объе­ме ВЫборКИ П->оо Гху*=Гху. Таким образом, требует-

х

у iL А	В	г y = b0+bjX
4. АНАЛИЗ РЕЗУЛЬТАТ01	3 ПАССИВНОГО ЭКСПЕРИМЕНТА…
В СВЯЗИ С ЭТИМ			[,' _________	Л
требуется проверка того,		у'	1 У
насколько значимо отли-		Л у/^ ''	'/'	Syi=const
чается выборочный ко-		L''
эффициент корреляции				-------- ►

х2

х3

xi

Рис.4.9. К понятию коэффициента парной корреляции в случае двумерного нормального распределения параметров

ся проверка значимости выборочного коэффициента парной корреляции и оценка его доверительного интервала.

Для определения значимости г_х„ сформулируем нуль-гипотезу Н₀: г_ху*=0, т.е. корреляция отсутствует. Для этого рассчитывается экспериментальное значение t-критерия Стьюдента

ху

t = г.

-Jn-2

(4.21)

и сравнивается с теоретическим при числе степеней свободы п-2.

Если t>t_a;n-2 при заданном уровне значимости а, то нулевая гипотеза от­клоняется, а альтернативная гипотеза H-i: г_ху* ф 0, о том, что коэффициент кор­реляции существенен, принимается.

Определение доверительного интервала коэффициента корреляции. При малых объемах выборки (п<20) можно рекомендовать построение доверитель­ного интервала для г_ху* , которое основано на преобразовании Р.Фишера. Он предложил такое нелинейное преобразование величины г_ху, при котором закон распределения этой оценки, вообще говоря, довольно сложный, практически приближается к нормальному. Это преобразование производится по формуле

ху

Z

|пг

1 1⁺^

Г

(4.22)

Среднеквадратичное отклонение случайной величины z* зависит от чис­ла опытов

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...

1
a ,• = -==, (4.23)

а математическое ожидание очень близко к числу, получающемуся после под­становки в формулу (4.22) вместо г_ху истинного значения коэффициента корре­ляции г_ху*. Эти свойства величины Z* позволяют просто оценить, в каких преде­лах может находиться истинное значение коэффициента корреляции, если по п опытам получены некоторые значения его выборочного значения (оценки) г_ху. Если граничное значение г_ху имеет тот же знак, что и г_ху*, то можно считать в первом приближении, что корреляционная связь между переменными досто­верна.

Пример 4.1.При обработке п=17 пар данных х и у выборочный коэффи­циент корреляции составил г_ху= - 0,94, т.е. величина у связана с х достаточно сильной причинной связью, близкой к функциональной зависимости. Требуется определить значимость и найти доверительный интервал выборочного коэф­фициента корреляции.

Определение значимости коэффициента г_ху

\ti-2 . . . V17-2
t = г , =0,94 . =10,6.

J^ — ir)² yl — (0,94)²

Критерий Стьюдента t₀,₀5;i5=2,13 (СТЬЮДРАСПОБР(0,05;15)=2,13145).

Поскольку t>t_a;n-2, то коэффициент корреляции существенен.

Определение доверительного интервала. По формулам (4.22) и (4.23)

определим величину Z*:

. 1, 1-0,94

Z =In------------- = -1,73о

2 1 + 0,94

и ее среднеквадратичное отклонение:

S * - . - - 0,267. ■^ л/17 — 3

Зададимся вероятностью того, что истинное значение Z отличается от вычисленного на основании оценки коэффициента корреляции Z* не более чем на 8z. Учитывая нормальный закон распределения Z, имеем при вероятности:

90%: 5z=1,64Sz =1,670,267=0,438;

95%: §z=1,960,267=0,523;

99,7%: 5z=3,000,267=0,801.

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

Таким образом, истинное значение Z лежит в пределах Zi < Z < Z₂, где с вероятностью, например, 90%, Zi= -1,738-0,438= -2,176 и Z₂= -1,738+0,438= -1,300. Для заданных значений вероятностей значения Zi и Z₂ составят:

90%: Zi= - 2,176, Z₂= -1,300;

95%: Zi= - 2,261, Z₂= -1,215;

99,7%: Zi= - 2,539, Z₂= -0,937.

Этим значениям Zi и Z₂ соответствуют коэффициенты корреляции, полу­ченные из формулы (4.22). Чтобы определить численные значения коэффици­ентов корреляции из формулы (4.22), можно воспользоваться инструментом «Подбор параметра» из электронных таблиц Microsoft Excel (меню «Сер­вис/Подбор параметра...»). В результате получим следующее решение:

90%: r-i= -0,97, г₂= -0,86, т.е. -0,97<г_ху<-0,86;

95%: r-i= -0,98, г₂= -0,84, т.е. -0,98<г_ху<-0,84;

99,7%: r-i= -0,99, г₂= -0,73, т.е. -0,99<г_ху<-0,73.

Следовательно, доверительные интервалы подтверждают достаточно сильную причинную связь между анализируемыми параметрами.

Таким образом, корреляционный анализ устанавливает связь между ис­следуемыми случайными переменными и оценивает тесноту этой связи.

Регрессионный анализ

Ниже излагаются основные положения регрессионного анализа, приме­нение которого для обработки результатов наблюдений связано с меньшим числом ограничений, чем при корреляционном анализе. Как и корреляционный анализ, регрессионный анализ включает в себя построение уравнения регрес­сии, например, методом наименьших квадратов и статистическую оценку ре­зультатов. Если в регрессионном анализе расчет коэффициентов ведется теми же методами, например наименьших квадратов, то его теоретические предпо­сылки требуют других способов статистической оценки результатов.

При проведении регрессионного анализа примем следующие допущения:

1) входной параметр х измеряется с пренебрежимо малой ошибкой. По­явление ошибки в определении у объясняется наличием в процессе не выяв-

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА…

ленных переменных и случайных воздействий, не вошедших в уравнение рег­рессии;

2) результаты наблюдений у_ь у₂,..., у,..., у_п над выходной величиной представляют собой независимые нормально распределенные случайные ве­личины;

3) при проведении эксперимента с объемом выборки п при условии, что каждый опыт повторен т* раз, выборочные дисперсии Si²,..., Si²,..., S_n² должны быть однородны. При выполнении измерений в различных условиях возникает задача сравнения точности измерений. При этом следует подчеркнуть, что экс­периментальные данные можно сравнивать только тогда, когда их дисперсии однородны. Это означает, как уже отмечалось (см. п. 3.5.1 и 3.5.2), принадлеж­ность экспериментальных данных к одной и той же генеральной совокупности. Напомним: однородность дисперсий свидетельствует о том, что среди сравни­ваемых дисперсий нет таких, которые с заданной надежностью превышали бы все остальные, т.е. была бы большая ошибка. При одинаковом числе парал­лельных опытов однородность дисперсии, как мы уже показали, можно оценить по критерию Кохрена, а для сравнения двух дисперсий целесообразно восполь­зоваться F-критерием Фишера (см. примеры 3.4-3.5).

После того как уравнение регрессии найдено, необходимо провести ста­тистический анализ результатов. Этот анализ состоит в следующем: проверя­ется значимость всех коэффициентов и устанавливается адекватность уравне­ния.

4. АНАЛИЗ РЕЗУЛЬТАТОВ ПАССИВНОГО ЭКСПЕРИМЕНТА...