Показательная форма комплексного числа
Правила умножения, деления и возведения в степень для комплексных чисел совпадают с аналогичными правилами для степенной функции, поэтому возможна запись комплексных чисел в тригонометрической
 и
и 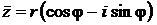
 и в показательной форме:
и в показательной форме:
 , и
, и 
соответственно.
Формулы (4.3) являются также формулами перевода комплексных чисел из алгебраической в показательную форму.
Умножение и деление комплексных чисел, заданных в показательной форме выполняются по формулам


Показательная форма не только обладает свойствами тригонометрической формы, но и позволяет производить дополнительные действия с комплексными числами (например, вычислить ii).
Задания для самостоятельной работы
1. Найти все значения корней.
1.1.  1.2.
1.2.  1.3.
1.3.  1.4.
1.4.  1.5.
1.5.  1.6.
1.6.  1.7.
1.7.  1.8.
1.8. 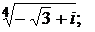 1.9.
1.9.  1.10.
1.10. 
2.Вычислить: 2.1.  2.2.
2.2. 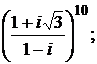 2.3.
2.3.  2.4.
2.4.  . 2.5.
. 2.5. 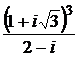 .
.
Вопросы для самоподготовки
Что называется числовой осью?
Какая числовая прямая называется расширенной?
3. Что называется модулем действительного числа?
4. Какое множество называется ограниченным?
5. Что такое нижняя и верхняя грани множества?
6. Что называется расстоянием между точками?
7. Какое множество называется окрестностью точки?
8. Что такое проколотая окрестность точки?
9. Какое число называется комплексным?
10. Геометрическое представление комплексных чисел.
11. Модуль и аргумент комплексного числа.
12. Формы представления комплексных чисел.
13. Как выполняется сложение и вычитание комплексных чисел, заданных в алгебраической форме?
14. Как выполняется умножение и деление комплексных чисел, заданных в алгебраической, тригонометрической и показательной формах?
15. Как возвести комплексное число в целую положительную степень?
16. Формула Муавра.
- Как извлекается корень целой положительной степени из комплексного числа?
Числовая последовательность и её предел
Определение. Если каждому натуральному числу n поставлено в соответствие число хn , то говорят, что этим определена последовательность чисел х1, х2, … , хn , … , которую обозначают {хn}.
хn - называют общим членом последовательности.
Например, 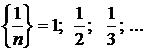
Из определения следует, что последовательность является функцией, отображающей множество N на R.
Определение. Если дана последовательность {хn} и из её членов образована новая последовательность, то она называется подпоследовательностью этой последовательности и обозначается  , kÎN.
, kÎN.
Определение. Последовательность {хn} называется ограниченной, если существует число С > 0 такое, что  для всех n >N.
для всех n >N.
Например, последовательность  ограничена, так как
ограничена, так как  ,С=1.
,С=1.
Предел последовательности
Пусть {хn} числовая последовательность.
Определение. Число а называется пределом числовой последовательности {хn} и обозначается
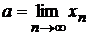 ,
,
если для любого положительного сколь угодно малого ε существует целое положительное  , такое, что для любого n≥N выполняется неравенство
, такое, что для любого n≥N выполняется неравенство  .
.
Определение. Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.
Последовательность {хn} будем называть бесконечно большой, если для любого  существует целое положительное N, такое, что для любого n≥N выполняется неравенство
существует целое положительное N, такое, что для любого n≥N выполняется неравенство  M.
M.
Пример:
Пусть 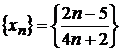 . Доказать, что число
. Доказать, что число  является пределом этой последовательности.
является пределом этой последовательности.
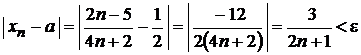 .
.
Найдем N, начиная с которого  выполняется для любого
выполняется для любого 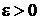 .
.
Для этого решим неравенство 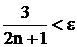 . Если
. Если 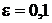 , то
, то  .
.
За N примем 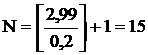 , где
, где  - целая часть числа а.
- целая часть числа а.
Начиная с номера 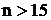 , выполняется неравенство
, выполняется неравенство  , то есть
, то есть  является пределом данной последовательности.
является пределом данной последовательности.
