Проекция вектора на ось и её свойства

Определение. Если на прямой задано направление, то она называется осью. Углом между двумя векторами (или между вектором и осью, или между двумя осями) называется наименьший угол φ, на который нужно повернуть один вектор (ось), чтобы он совпал по направлению с другим вектором (осью) (рис. 2.4).

Очевидно, что 0 ≤ φ ≤ π. Угол между векторами и 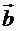обозначается ( ^ ).

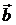Определение.Проекцией вектора на ось L называется длина отрезка А₁В₁, заключенного между ортогональными проекциями начала и конца вектора на эту ось, взятая со знаком плюс, если направление от А₁ к В₁ совпадает с направлением оси L, и со знаком минус, если не совпадает.

Из определения и рис. 2.5 следует, что проекция вектора на ось L равна

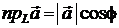. (2.3)

Направленный отрезок 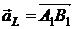называется ортогональной составляющей вектора по оси L. Если 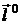– единичный вектор, соответствующий направлению оси L, то с учетом формулы (2.3)

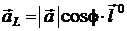. (2.4)

Проекции векторов и 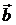на данную ось L обладают следующими свойствами:

;

.

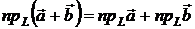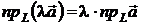Декартова система координат

Векторы будем рассматривать в реальном физическом пространстве, известном из элементарной математики как прямоугольная декартова система координат в R³, образованная тремя взаимно перпендикулярными осями X, Y, Z, называемых осями координат, и точки О – начало координат. Единичные векторы 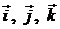, направленные вдоль осей X, Y, Z соответственно, образуют прямоугольный базис. Так как вектор 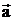свободный вектор, то совместим его начало с началом координат.

Известно, что каждый вектор 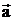пространства можно единственным образом разложить по векторам 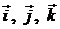(рис. 2.6):

. (2.5)

Числа x, y, z называются координатами вектора в базисе 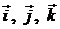. Этот факт будем записывать в виде , что равносильно разложению (2.5).

Геометрический смысл декартовых прямоугольных координат вектора выясняет следующее утверждение.

Теорема. 2.2. Декартовы прямоугольные координаты х, у, z вектора в базисе 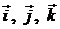являются его проекциями на соответствующие оси координат. (Доказательство теоремы предлагается выполнить самостоятельно).

Согласно теореме 2.1, при выполнении линейных операций над векторами тем же операциям подвергаются и координаты этих векторов, то есть если 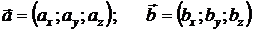, то

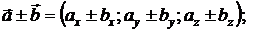
Если , , 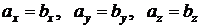то есть у равных векторов соответствующие координаты векторов равны.

Пример:

Даны три вектора 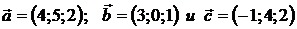, образующие базис. Найти координаты вектора в этом базисе.

Решение: из условия единственности разложения вектора в данном базисе следует, что , где α, β и γ некоторые неизвестные числа, одновременно неравные нулю.

Для определения α, β и γ, используя теорему (2.1) и условия равенства соответствующих координат у равных векторов, получим систему линейных уравнений:

Решив полученную систему линейных уравнений, получим координаты вектора в базисе векторов 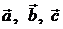: α = – 1, β = 4, γ = 3.

Ответ: .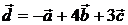

Направляющие косинусы вектора

Из теоремы 2.2. и рис. 2.6 следует, что

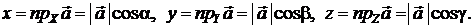(2.6)

По теореме Пифагора (см. рис. 2.6) имеем

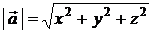. (2.7)

Три числа cosα, cosβ и cosγ называются направляющими косинусами вектора 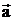. Из формул (2.6) и (2.7) имеем

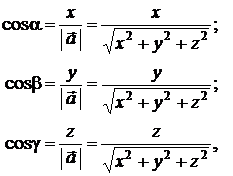, (2.8)

откуда

.

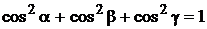Для единичного вектора , , 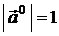учитывая равенства (2.8) получим:

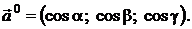
Пример:

Найти координаты орт вектора .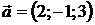

Решение: находим длину вектора : ; .

Тогда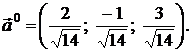

Условие коллинеарности двух векторов

Пусть 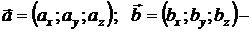коллинеарные векторы. Поскольку || , то для любого и (λ ≠ 0)

,

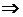
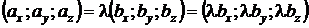отсюда

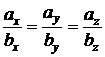. (2.9)

Итак, коллинеарность векторов 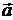и 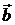равносильна пропорциональности соответствующих координат этих векторов (2.9).

Радиус-вектор и координаты точки

Радиус–вектором точки М назовём вектор , начало которого совпадает с началом системы координат (рис. 2.6). Очевидно, что всякая точка МÎR³ однозначно определяется своим радиус–вектором .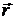

Координатами х, у, z точки М (рис. 2.6) называются проекции её радиус-вектора на координатные оси, то есть координатами точки являются коэффициенты разложения её радиус-вектора по базису :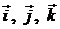

.

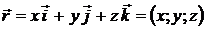При этом координата х называется абсциссой, у –ординатой, z –аппликатой точки М и обозначается М(х; у; z).

Рассмотрим две точки А(х₁;у₁;z₁) и В(х₂;у₂;z₂), радиус-векторы которых соответственно равны 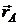и 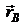(рис.2.7).

Так как 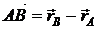, то .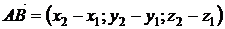

Отсюда, в частности, получаем формулу для вычисления расстояния между двумя точками А и В:

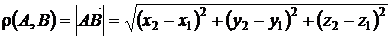(2.10)

Из формулы (2.10) следует, что длина радиус–вектора точки М вычисляется по формуле: