Линейная зависимость между векторами

Для характеристики взаимного расположения векторов в пространстве вводится понятие линейной зависимости между векторами.

Определение.Линейной комбинацией трёх векторов в пространстве называется вектор

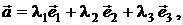
где l₁, l₂, l₃ некоторые действительные числа, называемые коэффициентами линейной комбинации. Говорят, что вектор ā разложен по векторам .

Определение.Векторы называются линейно-зависимыми, если существуют такие постоянные числа, одновременно не равные нулю (хотя бы один из них не равен нулю), что выполняется равенство

Если это равенство выполняется только для l₁ = l₂ = l₃ = 0, то векторы 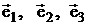называются линейно-независимыми.

Если – линейно-зависимые векторы, то один из них является линейной комбинацией остальных.

Например, l₃ ≠ 0, тогда 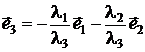. Это равенство говорит, что вектор является линейной комбинацией векторов и .

Примером линейной зависимости векторов могут быть два коллинеарных вектора и , так как в этом случае имеет место соотношение , где l– некоторое действительное число.

Из элементарной математики известно, что если и – два неколлинеарных вектора, то всякий компланарный им вектор однозначно представляется в виде линейной комбинации этих векторов (2.1)

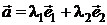. (2.1)

Отсюда следует, что любые три компланарных вектора линейно- зависимы.

Примером линейной независимости векторов могут быть три некомпланарных вектора , а любой четвертый вектор пространства единственным образом разлагается в их линейную комбинацию

. (2.2)

Равенство (2.2) означает, что любые четыре вектора в пространстве являются линейно-зависимыми.

Базис пространства и разложение вектора по базису

Определение.базисом пространства назовется совокупность линейно-независимых векторов, по которым можно разложить любой вектор этого пространства. В трехмерном пространстве это будет любая тройка некомпланарных векторов, на плоскости любая пара неколлинеарных векторов, а на прямой – любой ненулевой вектор. Векторы, составляющие базис называются базисными.

Таким образом, формула (2.1) представляет собой разложение вектора по базису на плоскости, а формула (2.2) – разложение вектора по базису в пространстве . Эти разложения единственны.

Коэффициенты l₁ , l₂ , l₃ в разложении (2.2) называются координатами вектора по базису . Аналогично интерпретируются коэффициенты l₁ и l₂ в равенстве (2.1).

Основное значение базиса состоит в том, что линейные операции над векторами в заданном базисе сводятся к обычным линейным операциям над числами – координатами векторов.

Теорема: 2.1.При сложении двух векторов и их соответствующие координаты суммируются. При умножении вектора на любое число l все его координаты умножаются на это число.

Доказательство. Пусть 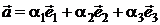и . Тогда в силу свойств линейных операций над векторами и единственности разложения вектора по базису получим