Системы обеспечения движения поездов»

РОСЖЕЛДОР

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный университет путей сообщения»

(ФГБОУ ВПО РГУПС)

А.И. Кирюнин

ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ

Задание на расчетно-графическую работу

С методическими указаниями

для студентов очной формы обучения специальности:

Системы обеспечения движения поездов»

Ростов–на–Дону

УДК 656.256

Кирюнин А.И.

Основы теории надежности: Задание на расчетно-графическую работу с методическими указаниями для студентов очной формы обучения специальности: 190901 «Системы обеспечения движения поездов». – Ростов н/Д: Рост. гос. ун-т путей сообщения, 2013. – 00 с.

Задание на расчетно-графическую работу с методическими указаниями составлено в соответствии с рабочей учебной программой по дисциплине: «Основы теории надежности» и предназначены для студентов очной формы обучения специальности 190901 «Системы обеспечения движения поездов».

Одобрено к изданию кафедрой: «Автоматика и телемеханика на железнодорожном транспорте» ФГБОУ ВПО РГУПС.

Табл. 0. Ил. 0. Библиогр.: 0 назв.

Рецензенты:

ã Ростовский государственный университет

путей сообщения, 2013

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

1.1. Количественные показатели надежности невосстанавливаемых систем

К числу количественных показателей надежности невосстанавливаемых систем относятся:

1. Вероятность безотказной работы за время 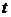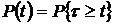, где 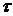–наработка до отказа; 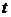– требуемое время безотказной работы (или время, для которого определяется 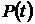). Статистическое (приближенное) значение этой вероятности, определяемое по результатам опытных испытаний, равно

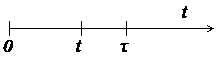
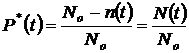
, (1.1.1)

где 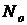– число однотипных объектов, поставленных на испытание;

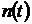– число отказавших объектов за время испытаний 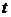(за интервал времени (0, t));

– число не отказавших объектов за время t, .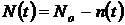

Далее везде знак * будет обозначать статистическое значение соответствующих показателей надежности.

2. Вероятность отказа объекта за время .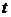

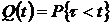, (1.1.2)

причем:

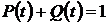и . (1.1.3)

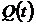– является функцией распределения случайной величины 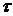(интегральным законом распределения случайной величины 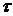или интегральным законом распределения отказов).

3. Плотность вероятности отказов (дифференциальная плотность (закон) распределения времени наработки до отказа 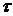, дифференциальная функция распределения случайной величины )

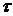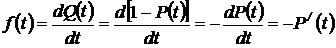. (1.1.4)

Из (1.1.4) имеем:

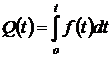, (1.1.5)

, (1.1.6)

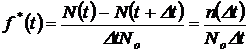1/ч, (1.1.7)

где 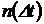– число отказавших объектов на интервале времени : от t до .

Экспоненциальный закон распределения времени наработки до отказа 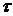(когда 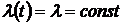) определяется формулой

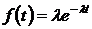. (1.1.8)

4. Интенсивность отказов:

1/ч, (1.1.9)

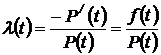, (1.1.10)

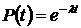, (1.1.11)

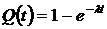, (1.1.12)

5. Средняя наработка до отказа .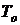

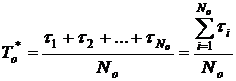, ч (1.1.13)

где – время наработки до отказа 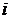–го образца .

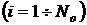. (1.1.14)

ОФОРМЛЕНИЕ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

Расчетно-графическая работа должна иметь следующий состав: титульный лист, содержание, введение, задача № 1, задача № 2, …, задача № 5, заключение, список использованных источников. Пример оформления титульного листа расчетно-графической работы приведен в приложении А.

Графический материал работы оформляются в виде рисунков в составе соответствующих задач.

Расчетно-графическая работа выполняется на листах писчей бумаги формата А4 (210×297 мм) с полями по всем четырем сторонам листа (без рамки). Размеры левого поля – не менее 30 мм, верхнего и нижнего – не менее 20 мм, правого – не менее 10 мм. Текст работы выполняется на одной стороне листа: пишется от руки (высота букв и цифр должна быть не менее 2,5 мм) или печатается с использованием компьютера и принтера (размер шрифта – не менее 12 пт).

Общий объем расчетно-графической работы: 10 – 20 листов формата А4. Листы работы должны быть пронумерованы (за исключением титульного листа и содержания).

Расчетно-графическая работа должна быть оформлена в соответствии с требованиями ГОСТ ЕСКД и СТП РГУПС.

При наличии замечаний исправления делаются на чистой стороне листа (оборотной стороне предыдущего листа) рядом с допущенной ошибкой.

3. ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ

Целью расчетно-графической работы является закрепление теоретических сведений и получение практических навыков по расчету надежности систем обеспечение движения поездов.

Перед выполнением расчетно-графической работы необходимо изучить теоретические основы, изложенные в разделе 1; ознакомиться с рекомендуемой литературой, перечень которой указан в конце настоящих методических указаний.

Расчетно-графическая работа включает в себя 5 (пять) задач. Решение задач рекомендуется выполнять в той же последовательности, как они поставлены.

Указания по выбору варианта содержаться в условии каждой задачи.

Для каждой задачи приведен типовой пример ее решения.

Задача № 1 На испытание поставлено N₀ однотипных изделий. За время t часов отказало n(t) изделий. За последующий интервал времени Δt отказало n(Δt) изделий. Необходимо вычислить статистические значения вероятности безотказной работы за время t и t+Δt, частоты отказов и интенсивности отказов за время t. Исходные данные для решения задачи приведены в табл. 3.1. Номер варианта определяется двумя последними цифрами номера зачетной книжки студента.

Таблица 3.1

Предпоследняя цифра номера	Последняя цифра номера	N0	t, час	Δt	n(t)	n(Δt)
Четная или 0
Нечетная

Типовой пример. На испытание поставлено 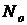= 2000 однотипных изделий. За время 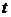= 4000 часов отказало 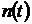= 100 изделий, а за последующие 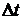= 100 часов отказало еще 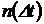= 10 изделий (см. рис 1). Определить статистические значения показателей надежности: , ; ; ; ; .

		Рис. 3.1

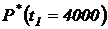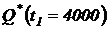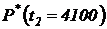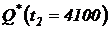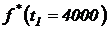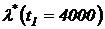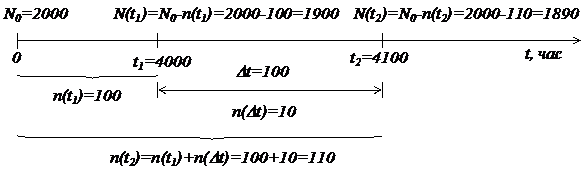Решение

1. По формулам (1.1.1) и (1.1.2) определяем вероятности безотказной работы 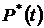и отказа 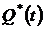за время испытаний 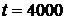час:

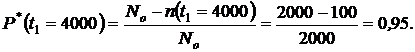
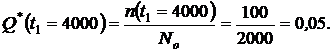
или из формулы (1.1.3):

.

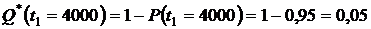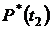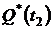2. Определяем и за время испытаний :

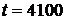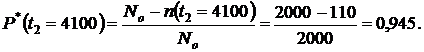
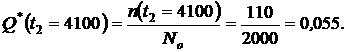
или из формулы (1.1.3):

.

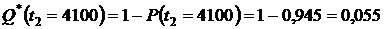3. Определяем 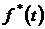за время 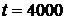час по формуле (1.1.7):

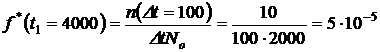1/ч.

4. Определяем 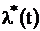за время 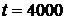по формуле (1.1.9):

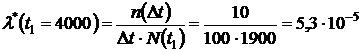1/ч.

Задача № 2 Структурная схема надежности устройства для различных вариантов приведена на рис. 3.2. Номер варианта определяется двумя последними цифрами номера зачетной книжки студента. Интенсивности отказов элементов имеют следующие значения: λ₁=n₁∙10^-4 1/час; λ₂=n₂∙10^-4 1/час; 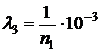1/час; 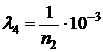1/час, где n₁ – последняя цифра номера зачетной книжки (цифра 0 соответствует n₁=10); n₂ – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n₂=10). Показатели надежности устройства распределены по экспоненциальному закону распределения. Необходимо найти среднюю наработку до отказа устройства и вероятность его безотказной работы в течение 100 часов.

Рис. 3.2

Типовой пример. Структурная схема надежности устройства приведена на рис. 3.3. Интенсивности отказов элементов имеют следующие значения:

Рис. 3.3

λ₁=0,23∙10^-3 1/час; λ₂=0,5∙10^-4 1/час; λ₃=0,4∙10^-3 1/час. Показатели надежности устройства распределены по экспоненциальному закону распределения. Необходимо найти среднюю наработку до отказа устройства .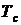

Решение.

1. Готовой формулы для средней наработки до отказа в рассматриваемом случае нет. Поэтому необходимо воспользоваться соотношением:

.

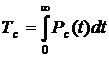2. Найдем выражение для вероятности безотказной работы 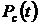устройства. Очевидно, что

,

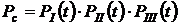где ,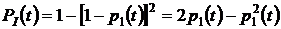

,

.

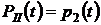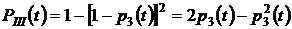Тогда, подставляя значения 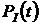, 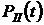и 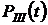в выражение для 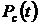,получим:

.

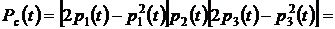
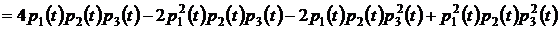Так как 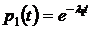, , 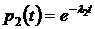, 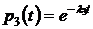то

.

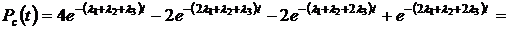
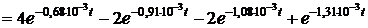3. Определяем среднюю наработку до отказа:

.

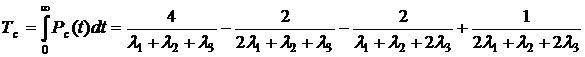Подставляя в выражение для 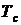значение интенсивности отказов из условия задачи, получаем:

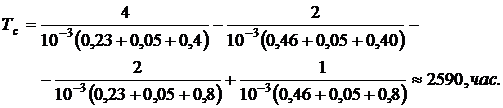
Задача № 3 Необходимо выполнить ориентировочный расчет надежности системы, состоящей из N элементов различного типа. Требуется вычислить вероятность безотказной работы системы в течение времени t и среднюю наработку до отказа системы Т_ср.

Расчет следует выполнить по данным о надежности элементов, приведенным в приложении Б.

Таблица 3.2

Наименование и количество элементов

Предпоследняя цифра номера

Резисторы R

Конденсаторы С

Диоды D

Транзисторы Т

Силовые трансформаторы, шт

Дроссели, шт

L, шт

Время работы t, час

тип

шт

тип

шт

тип

шт

тип

шт

ВС-0,25

слюдяные

выпрямительные точечные германиевые

мощные низкочастотные

Nст

ВС-0,5

танталовые

маломощные низкочастотные германиевые

ВС-1

МЛТ-0,5

керамические

выпрямительные точечные германиевые

мощные низкочастотные

Nст

МЛТ-1

танталовые

маломощные низкочастотные германиевые

МЛТ-2

МЛТ-0,25

слюдяные

выпрямительные плоскостные

маломощные низкочастотные кремниевые

Nст

–

МЛТ-1

керамические

танталовые

МЛТ-0,25

слюдяные

выпрямительные точечные кремниевые

маломощные низкочастотные кремниевые

Nст

–

МЛТ-0,5

МЛТ-1

МЛТ-0,25

керамические

выпрямительные точечные германиевые

маломощные германиевые низкочастотные

Nст

МЛТ-0,5

танталовые

ПКВ-2

МЛТ-0,25

керамические

выпрямительные точечные кремниевые

мощные высокочастотные германиевые

Nст

ПКВ-2

танталовые

ВС-0,25

керамические

импульсные точечные

маломощные низкочастотные германиевые

Nст

МЛТ-1

танталовые

МЛТ-2

МЛТ-0,5

слюдяные

выпрямительные плоскостные

мощные низкочастотные

Nст

–

МЛТ-1

танталовые

МЛТ-0,5

бумажные

выпрямительные повышенной мощности

мощные низкочастотные

Nст

–

СПО-2

ПЭВ-10

МЛТ-0,25

керамические

выпрямительные точечные германиевые

маломощные низкочастотные германиевые

Nст

МЛТ-0,5

танталовые

ПКВ-2

Исходные данные для решения задачи приведены в табл. 3.2. Количество силовых трансформаторов N_ст соответствует последней цифре номера зачетной книжки студента (цифра 0 соответствует N_ст=10).

Номер варианта определяется двумя последними цифрами номера зачетной книжки студента.

Типовой пример. Система состоит из 14 маломощных низкочастотных германиевых транзисторов, 4 плоскостных кремниевых выпрямителей, 56 керамических конденсаторов, 168 резисторов типа МЛТ мощностью 0,5 Вт, 1 силового трансформатора, 2 накальных трансформаторов, 6 дросселей и 3 катушки индуктивности. Необходимо найти вероятность безотказной работы системы в течение t=260 час и среднюю наработку до отказа системы Т_с.

Решение.

1. Для выполнения ориентировочного расчета надежности составим и заполним табл. 3.3, вычислив величину интенсивности отказов изделия. Значения интенсивностей отказов λ_i элементов (графа 4) выбирается из таблиц приложения Б.

Таблица 3.3

Наименование и тип элемента	Обозначение на схеме	Количество элементов Ni	Интенсивность отказов, 10-5 1/час	Ni ∙ λi × 10-5, 1/час	Примечание
1. Транзистор маломощный низкочастотный кремневый	VT1 – VT14		0,3	4,2	Табл. Б.3
2. Диод выпрямительный плоскостной	VD1 –VD4		0,5		Табл. Б.3
3. Конденсатор керамический	C1 – C56		0,14	7,84	Табл. Б.2
4. Резистор МЛТ, 0,5 Вт	R1 – R168		0,05	8,4	Табл. Б.1
5. Трансформатор силовой	Т1		0,3	0,3	Табл. Б.4
6. Трансформатор накальный	Т2, Т3		0,2	0,4	Табл. Б.4
7. Дроссель	L1 – L6		0,1	0,6	Табл. Б.4
8. Катушка индуктивности	L7 – L9		0,05	0,15	Табл. Б.4

2. Вычисляем суммарную интенсивность отказов системы:

.

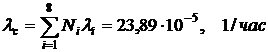3. Вычисляем вероятности безотказной работы системы за время t=260 часов:

.

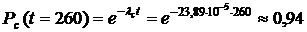4. Вычисляем среднюю наработку до отказа системы:

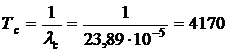, час.

Задача № 4 Для графа состояний восстанавливаемой резервированной системы, изображенного на рис. 3.4 (в соответствии с вариантом: номер варианта определяется двумя последними цифрами номера зачетной книжки студента) необходимо: определить способ структурного резервирования, кратность резервирования, начертить ССН системы, вычислить коэффициент готовности системы К_Г, сделать вывод о необходимости увеличения кратности резервирования системы. Исходные данные для расчета: К_Гзад=0,999; λ=n₁∙10^-4 1/час; μ=n₂∙10^-4 1/час, где n₁ – последняя цифра номера зачетной книжки (цифра 0 соответствует n₁=10); n₂ – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n₂=10).

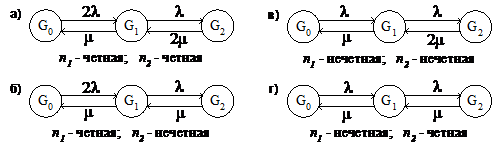
Рис. 3.4.

На рис. 3.4 приняты следующие обозначения: G₀ и G₁ – работоспособные состояния системы; G₂ – неработоспособное состояние; Р_i – вероятность нахождения системы в i-ом состоянии; λ – интенсивность отказа; μ – интенсивность восстановления.

Типовой пример. Система обеспечения движения поездов имеет общее резервирование замещением кратности m=1. Интенсивность отказов нерезервированной системы равна λ=0,001 1/ч, а интенсивность восстановления – μ=0,1 1/ч. Необходимо вычислить коэффициент готовности восстанавливаемой резервированной системы К_Г, если заданное значение коэффициента готовности равно К_Гзад = 0,999, а восстановление работоспособного состояния системы является ограниченным.

Решение

1. Чертим структурную схему надежности восстанавливаемой резервированной системы (рис. 3.5)

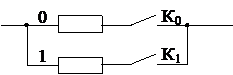Рис. 3.5

2. Чертим граф состояний системы (рис. 3.6)

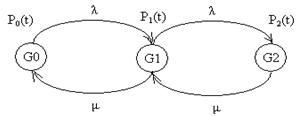
Рис. 3.6

3. С использованием полученного графа состояний системы записываем систему линейных алгебраических уравнений по указанным в разделе 1 правилам (правилам составления дифференциальных уравнений Колмогорова А.Н.):

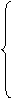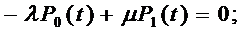
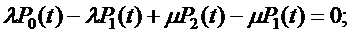
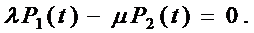
Полученная система уравнений является линейно зависимой.

4. Приводим данную систему уравнений к системе линейно независимых уравнений путем исключения второго уравнения и добавления нормировочного уравнения:

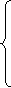
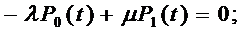
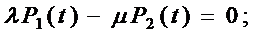
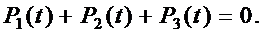
5. Используя полученную систему уравнений, составляем и вычисляем определители D и D_i (i=0, 1, 2):

P0 P1 P2

	P0 P1 P2

	P0 P1 P2

	P0 P1 P2

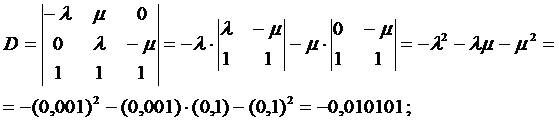
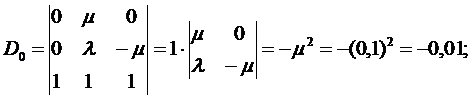
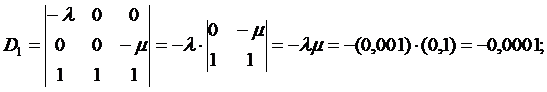
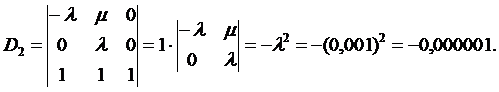
6. Вычисляем вероятности нахождения восстанавливаемой резервированной системы в соответствующих состояниях G₀, G₁, G₂:

;

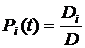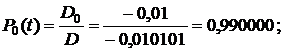
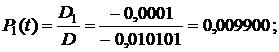
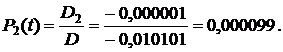
7. Вычисляем коэффициент готовности:

К_Г=P₀(t)+P₁(t)=0,990000+0,009900=0,9999.

Вывод. Вычисленное значение коэффициента готовности превышает заданное значение ( 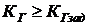). Следовательно, кратность резервирования m=1 является достаточной.

Задача № 4 Для восстанавливающего органа (ВО) типа 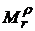(в соответствии с вариантом: номер варианта определяется двумя последними цифрами номера зачетной книжки студента) запишите логическую функцию (функцию алгебры логики) и постройте структурную схему на основе логических элементов «И», «ИЛИ». Определите количество отказов по «0» и «1», которое может корректировать восстанавливающий орган данного типа. 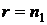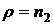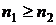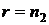Исходные данные: и , если или и 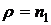, если 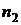> 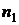, где n₁ – последняя цифра номера зачетной книжки (цифра 0 соответствует n₁=10); n₂ – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n₂=10).

Типовой пример. Для восстанавливающего органа (ВО) типа 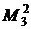запишите логическую функцию (функцию алгебры логики) и постройте структурную схему на основе логических элементов «И», «ИЛИ». Определите количество отказов по «0» и «1», которое может корректировать восстанавливающий орган данного типа.

Решение

1. В соответствии с условием: 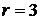и 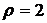(так как знак мажоритирования в общем виде записывается как: ).

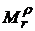2. Определяем число корректируемых отказов по «1» ВО типа :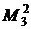

n₁ = ρ – 1 = 2 – 1 = 1.

3. Определяем число корректируемых отказов по «0» ВО типа :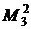

n_о = r – ρ = 3 – 2 = 1.

4. В соответствии с выражением:

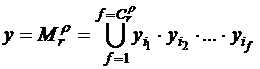
запишем логическую функцию (функцию алгебры логики) ВО 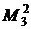в дизъюнктивной нормальной форме:

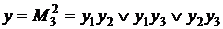
Количество логических слагаемых в данной функции определяется числом сочетаний 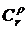(в данном случае: 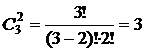), а количество логических сомножителей в каждом слагаемом определяется значением 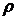(в данном случае: ):

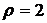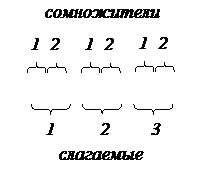
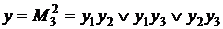
5. В соответствии с правилами синтеза комбинационных схем на булевом базисе (логические элементы «И», «ИЛИ», «НЕ») структурная схема ВО типа 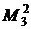для полученной логической функции будет иметь вид (рис. 9):

Рис. 3.7

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Сапожников В.В., Сапожников Вл.В., Шаманов В.И. Надежность систем железнодорожной автоматики, телемеханики и связи: Учебное пособие для вузов ж.д. трансп. / Под ред. Вл.В. Сапожникова. – М.: Маршрут, 2003, – 263 с.

2. Сапожников В.В. и др. Теоретические основы железнодорожной автоматики, телемеханики и связи / В,В, Сапожников, Ю.А. Кравцов, Вл. В. Сапожников. – М.: Транспорт, 1995. – 320 с.

3. Половко А.М., Гуров С.В. Основы теории надежности. – СПб.: БХВ-Петербург, 2006. – 704 с.

4. Половко А.М., Гуров С.В. Основы теории надежности. Практикум. – СПб.: БХВ-Петербург, 2006. – 560 с.

5. Гнеденко Б.В. и др. Математические методы в теории надежности / Б.В. Гнеденко, Ю.К. Беляев, А.Д. Соловьев. – М.: Наука, 1965. – 524 с.

6. Козлов Б.А., Ушаков И.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. – М.: Советское радио, 1975. – 472 с.

7. Дружинин Г.В. и др. Теория надежности радиоэлектронных систем в примерах и задачах / Г.В. Дружинин, С.В. Степанов, В.Л. Шахматова, Г.А. Ярыгин. – М.: Энергия, 1976. – 448 с.

8. Половко А.М. и др. Сборник задач по теории надежности / А.М. Половко, И.М. Маликов, А.Н. Жигарев, В.И. Зарудный; Под ред. А.М. Половко и И.М. Маликова. – М.: Советское радио, 1972. – 408 с.

ПРИЛОЖЕНИЕ А

Пример выполнения титульного листа пояснительной записки

курсового проекта

РОСЖЕЛДОР

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный университет путей сообщения»

(ФГБОУ ВПО РГУПС)

Кафедра «Автоматика и телемеханика на железнодорожном транспорте»

РАСЧЕТ НАДЕЖНОСТИ

ПРИЛОЖЕНИЕ Б

Таблица Б.1

Номинальная интенсивность отказов резисторов при Тº=+20ºС и К_н=1

Тип резисторов	Номинальная мощность рассеяния Рном, Вт
0,25	0,5
Интенсивность отказов λ0×10-6 1/час
Непроволочные	МЛТ	0,4	0,5	1,0	1,6	-	-	-	-	-	-	-	-	-	-
ТВО	0,4	0,45	0,8	1,4	2,2	3,0	-	4,0	-	-	-	6,0	-	-
МОУ	0,5	0,55	1,1	1,5	2,3	3,1	-	-	4,2	-	5,5	-	-
МУН	0,6	0,6	1,2	2,0	-	-	-	-	-	-	-	-	-	-
УНУ	0,6	0,7	1,2	1,7	2,3	3,0	-	-	4,8	-	8,0	-	-
КЭВ	0,6	0,75	1,3	1,75	2,4	3,1	-	-	5,0	-	-	-	-	-
ВС	0,7	0,8	1,35	1,8	2,5	3,3	-	-	-	-	-	-	-	-
УЛИ	0,6	0,65	1,3	-	-	-	-	-	-	-	-	-	-	-
БЛП	0,7	0,75	1,4	-	-	-	-	-	-	-	-	-	-	-
СПО	0,6	0,7	1,15	1,8	-	-	-	-	-	-	-	-	-	-
СП	0,7	0,8	1,3	2,0	-	-	-	-	-	-	-	-	-	-
Проволочные	ПТН	-	1,1	1,4	1,8	-	-	-	-	-	-	-	-	-	-
ПКВ	-	1,2	1,5	2,0	2,5	-	-	-	-	-	-	-	-	-
ПЭВ	-	1,6	2,0	2,6	2,9	3,2	3,5	-	4,5	5,0	5,6	-	8,0
ПТП	-	-	2,2	2,6	3,0	-	-	-	-	-	-	-	-	-
РП	-	-	-	3,0	-	-	-	-	4,7	-	-	-	8,5	-

Таблица Б.2

Номинальные интенсивности отказов конденсаторов при Тº=+20ºС и К_н=1

Тип конденсатора	Интенсивность отказов λ0×10-6 1/час
бумажные	1,8
металлобумажные	2,0
слюдяные	1,2
стеклянные	1,6
керамические	1,4
пленочные	2,0
электрические алюминиевые	2,4
электрические танталовые	2,2

Таблица Б.3

Номинальные интенсивности отказов полупроводниковых приборов при Тº=+20ºС и К_н=1

Полупроводниковые приборы	Интенсивность отказов λ0×10-6 1/час приборов
германиевых	кремниевых
Диоды	Выпрямительные точечные	0,7
Выпрямительные микроплоскостные	–	0,7
Выпрямительные плоскостные	–
Выпрямительные плоскостные повышенной надежности	–	2,5
Выпрямительные повышенной мощности	–
Импульсные точечные		-
Импульсные плоскостные мезадиодны		2,5
Импульсные сплавные	–	0,6
Управляемые	–
Стабилитроны	–
Варикапы	–
Выпрямительные столбы	–
Микромодульные	4,2	4,5
Транзисторы	Маломощные низкочастотные
Мощные низкочастотные	4,6	–
Маломощные высокочастотные	2,6	–
Мощные высокочастотные		1,7
Микромодульные		–

Таблица Б.4

Номинальная интенсивность отказов трансформаторов и моточных изделий (дроссели, катушки индуктивности и др.) при Тº=+20ºС и К_н=1

Трансформаторы и моточные изделия	Интенсивность отказов λ0×10-6 1/час
Автотрансформаторы	5,0
Силовые	3,0
Высоковольтные	4,0
Накальные анодные	2,0
Импульсные	0,5
Дроссели	1,0
Катушки индуктивности	0,5

Таблица Б.5

Номинальные интенсивности отказов некоторых микроэлектронных элементов при Тº=+20ºС и К_н=1

Наши рекомендации

Элемент	Интенсивность отказов λ0, 1/час
Интегральная схема	0,2∙10-7
Резистор	0,1∙10-7
Конденсатор керамический	0,3∙10-7
Паяные соединения ножек элементов на печатной плате	0,5∙10-7
Контакт разъема	0,2∙10-7
Печатная плата /на один слой/	10-7
Соединение