Приближенные вычисления с помощью полного дифференциала

Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

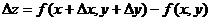
Если подставить в эту формулу выражение

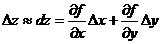
то получим приближенную формулу:

Пример. Вычислить приближенно значение , исходя из значения функции при x = 1, y = 2, z = 1.

Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01,

Dz = 1,02 – 1 = 0,02.

Найдем значение функции u(x, y, z) =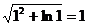

Находим частные производные:

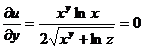
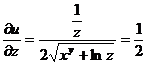
Полный дифференциал функции u равен:

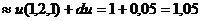
Точное значение этого выражения: 1,049275225687319176.

Частные производные высших порядков

Если функция f(x, y) определена в некоторой области D, то ее частные производные 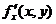и 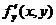тоже будут определены в той же области или ее части.

Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второго порядка.

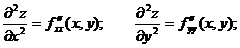
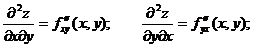
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение. Частные производные вида 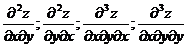и т.д. называются смешанными производными.

Экстремум функции нескольких переменных

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой максимума.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

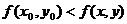
то точка М₀ называется точкой минимума.

Теорема. (Необходимые условия экстремума).

Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует.

Эту точку (х₀, у₀) будем называть критической точкой.

Теорема. (Достаточные условия экстремума).

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

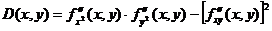
1) Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

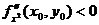- максимум, если 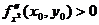- минимум.

2) Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

Условный экстремум

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение

j(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

В точках экстремума:

=0

(1)

Кроме того:

(2)

Умножим равенство (2) на число l и сложим с равенством (1).

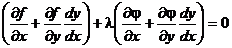
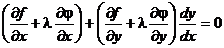
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

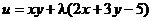
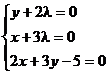
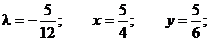
Таким образом, функция имеет экстремум в точке .

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Производная по направлению

Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М₁( x + Dx, y + Dy, z + Dz).

Проведем через точки М и М₁ вектор . Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются направляющими косинусамивектора .

Расстояние между точками М и М₁ на векторе обозначим DS.

Высказанные выше предположения, проиллюстрируем на рисунке:

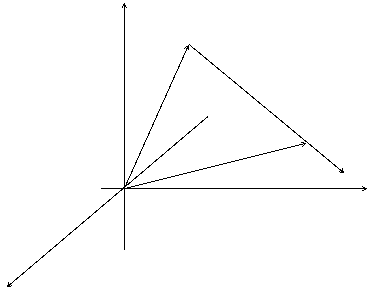z

M

M₁

y

x

Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:

,

где величины e₁, e₂, e₃ – бесконечно малые при .

Из геометрических соображений очевидно:

Таким образом, приведенные выше равенства могут быть представлены следующим образом:

;

Заметим, что величина s является скалярной. Она лишь определяет направление вектора .

Из этого уравнения следует следующее определение:

Определение: Предел называется производной функции u(x, y, z) по направлению вектора в точке с координатами ( x, y, z).

Пример. Вычислить производную функции z = x² + y²x в точке А(1, 2) по направлению вектора 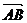. В (3, 0).

Решение. Прежде всего необходимо определить координаты вектора .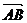

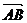=(3-1; 0-2) = (2; -2) = 2 .

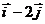Далее определяем модуль этого вектора:

=

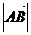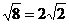
Находим частные производные функции z в общем виде:

Значения этих величин в точке А :

Для нахождения направляющих косинусов вектора 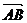производим следующие преобразования:

=

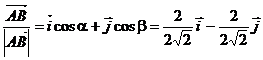
За величину принимается произвольный вектор, направленный вдоль заданного вектора, т.е. определяющего направление дифференцирования.

Отсюда получаем значения направляющих косинусов вектора :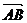

cosa = ; cosb = -

Окончательно получаем: 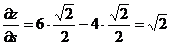- значение производной заданной функции по направлению вектора .

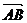Градиент

Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке

,

то этот вектор называется градиентомфункции u.

При этом говорят, что в области D задано поле градиентов.