Специальные и большие системы линейных уравнений.

1) совместные системы: число уравнений (m) равно числу неизвестных (n) n = m

2) несовместные (переопределенные): n < m

3) недоопределенные (несовместные): n > m

Переопределенные системы уравнений могут быть решены методом минимизации суммы квадратов уклонений:

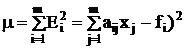
R – неизвестных, m – уравнений.

Систему можно записать:

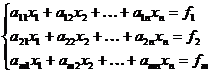
Решение системы уравнений методом минимизации суммы квадратов уклонений сводится к умножению слева обеих частей уравнения на транспонирующую матрицу коэффициентов:

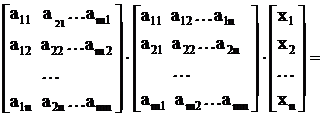
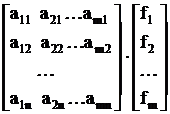
Такое преобразование позволяет от переопределенной системы уравнений перейти к определенной системе уравнений. Т.е. из системы с m уравнениями мы получим систему с n уравнениями и n неизвестными.

При решении переопределенной системы речь идет о нахождении наилучшего приближения.

Пример:

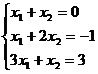
Решаем методом минимизации:

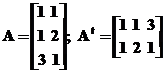
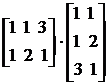
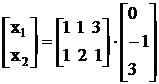
В итоге имеем:

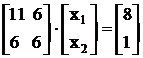
Запишем систему в развернутом виде:

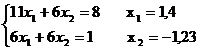
Находим m:

m = (х₁ + х₂)² + (х₁ + 2х₂ + 1)² + (3х₁ + х₂ – 3)² » 0,033

Меньшее значение m методом минимизации суммы квадратов отклонений получить нельзя.

Метод минимизации суммы квадратов уклонений при решении системы уравнений позволяет эффективно использовать исходную информацию, если она имеется в избытке.

Недоопределенная система: m < n

Имеется бесконечное множество решений, например можно задаться значениями m – n неизвестных и затем точно найти оставшиеся m неизвестных, решая m уравнений.

Возможно решение недоопределенной системы уравнений при введении новых неизвестных y: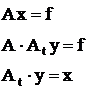

Пример:

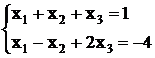
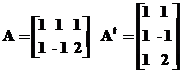
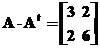
В итоге имеем такую систему уравнений

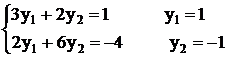
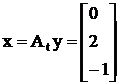переходим к старым неизвестным:

х₁ = 0; х₂ = -2; х₃ = -1

Применение методов теории вероятности

В расчетах электроэнергетики

Случайность – непознанная закономерность

Народная мудрость.

Случайные величины

Теория вероятности – это наука, изучающая закономерности случайных явлений. Невозможность учесть причины якобы случайных явлений (кз) приводит к необходимости использовать теорию вероятностей.

Случайное событие – это событие, которое в результате опыта может произойти или не произойти.

Достоверное событие – это событие, которое произойдет обязательно.

Невозможное событие – это событие, которое не может произойти.

Вероятность – численная степень возможности появления случайного события в данном опыте.

Р(А) – вероятность А

Р(А) = 1 достоверное событие

Р(А) = 0 невозможное событие

0 £ Р(В) £ 1

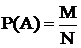
М – благоприятные случаи появления события А;

N – общее число случаев; (Это классическое определение вероятности)

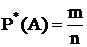- статистическое определение вероятности.

n – количество проведенных опытов

m – количество опытов в которых произошло событие А

Несколько событий называются несовместными, если никакие хотя бы 2 из них не могут произойти одновременно. В противном случае события – совместные.

Равновозможные события – это события, вероятность появления которых можно считать одинаковой.

Несколько событий, одно из которых наверняка произойдет образуют полную группу событий, причем эти события несовместны.

Если событие состоит в том, что событие А не происходит, то это противоположное событие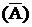

Зависимые события – если вероятность некоторого события зависит от того произошло или нет событие А, то эти события называются зависимыми. Если нет, то независимыми.

Вероятность события В после того, как произошло событие А – условная вероятность.

Р(В/А)

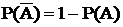
Умножение обозначает совметные события «и», плюс – обозначает «или».