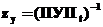Метод независимых напряжений

_®

Г_tU = 0 всего неизвестных напряжений р (столько, сколько ветвей)

неизвестных напряжений > чем уравнений.

p > n

где n – число уравнений по числу независимых контуров

разделим вектор напряжений на 2 вектора.

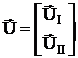
В первый вектор включим столько составляющих, сколько независимых узлов.

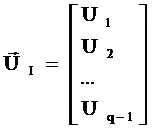
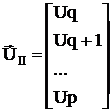
Напряжения, входящие в первый вектор будем считать независимыми напряжениями, если через них можно выразить все остальные напряжения электрической схемы.

Соответствующую матрицу контуров делим на 2 подматрицы

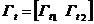
В итоге получим уравнение:

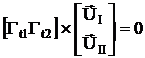
Запишем это уравнение в развернутом виде

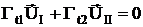
Находим из этого уравнения :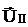

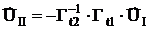
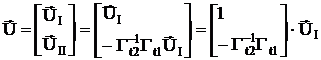
По независимым напряжениям можно найти все напряжения схемы

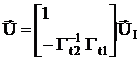
Воспользуемся для нахождения независимых напряжений 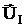первым законом Кирхгофа, запиcанным в системе напряжений (см. стр. 8)

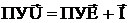закон Кирхгофа в системе напряжений

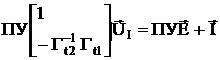
Уравнение независимых напряжений

Вводим обозначения

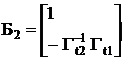матрица преобразований независимых напряжений

К₂=ПУ Матрица преобразования источников ЭДС в соответствии имеющихся эквивалентных источников тока

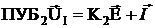
Y₁=ПУБ₂ Матрица проводимости в методе независимых напряжений

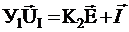
Пример Метод независимых напряжений

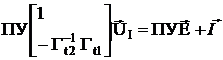
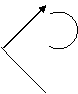независимых узлов

q - 1=4

II

независимых напряжений 4

IY

Выбираем:

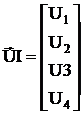
Независимые напряжения необходимо выбрать таким образом, чтобы они не образовали ни одного замкнутого контура. В обратном случае матрица Г_t2 будет особенной и задача не будет иметь решения.

Независимые напряжения образуют дерево электрической схемы. Все остальные называются хордами

Составляем матрицу контуров

1 2 3 4 5 6 7 8

1 2 0 1 0 0 1 0 I

Г_t= Г_t1 Г_t2 = 0 –1 -1 0 1 0 0 0 II

0 0 1 –1 0 1 0 0 III

0 0 0 0 0 -1 -1 1 IY

Матрицу Б₂ можно составить не выполняя вычислений

U₁ U₂ U₃ U₄

1 0 0 0 U₁

0 1 0 0 U₂

1 0 0 1 0 U₃

Б₂ = -Г_t2^-1Г_t1 0 0 0 1 U₄

0 1 1 0 U₅

0 0 -1 1 U₆

-1 -1 0 -1 U₇

-1 -1 -1 0 U₈

Напряжение с 5-го по 8-е нужно выразить через независимые напряжения и полученные при независимых напряжениях коэффициенты перенести на соответствующие места матрицы:

U₅ – U₃ – U₂ = 0

U₅ = U₂ + U₃

U₆ = -U₃ + U₄

U₇ = -U₁ – U₂ – U₄

U₈ = -U₁ – U₂ – U₃

Таким образом имеем систему уравнений с четырьмя неизвестными независимыми напряжениями. Решая ее находим независимые напряжения. Все остальные напряжения можно найти используя соотношения

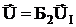
Метод узловых напряжений

Это частный метод. Он получен из метода независимых напряжений.

Недостаток метода независимых напряжений в том, что в общем случае матрица проводимостей У₁ является несимметричной. Для ее нахождения необходимо найти производную трех матриц.

Y₁ = ПYБ₂

Расчеты упрощаются при выполнении условия

Б₂ = П_t

Тогда получим матрицу узловых проводимостей

Y_у = ПYП_t

А вектору независимых напряжений будет соответствовать вектор узловых напряжений

_→

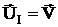
Матрица У_у является симметричной и может быть легко получена непосредственно из электрической схемы.

В итоге имеем уравнение _{→ → →}

ПYП_t V = ПYЕ + I

_{→ → →}

Y_yV = ПYЕ + I

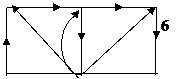
Пример:

q –1 =3 (независимые узлы)

V1

V3

V2

D

C

B

A

( независимые напряжения)

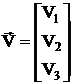
Y₁₁ Y₁₂ Y₁₃

Y_у = Y₂₁ Y₂₂ Y₂₃

Y₃₁ Y₃₂ Y₃₃

Для нахождения проводимостей, расположенных по главной диагонали необходимо сложить проводимости ветвей, входящих в рассматриваемый узел.

Y₁₁ = Y₁ + Y₂ + Y₃

Y₂₂ = Y₂ + Y₄ + Y₅

Y₃₃ = Y₃ + Y₅ + Y₆

Для нахождения проводимостей, которые находятся вне главной диагонали необходимо их приравнять с обратным знаком к проводимостям ветвей, соединяющих рассматриваемые узлы.

Y₁₂ = - Y₂; Y₂₁ = - Y₂

и т.д.

В итоге получим систему из 3-х уравнений с тремя неизвестными узловыми напряжениями. Определив узловые напряжения, можно найти все напряжения ветвей электрической схемы:

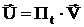
К расчету электрических токов:

Вектор тока можно найти, если известны контурные токи.

Из метода контурных токов:

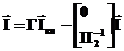
А контурные токи находим из контурных уравнений

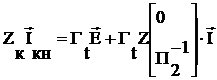
Отсюда найдем 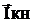- вектор контурных токов

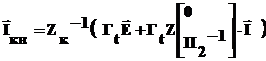
z_к = Г_t z Г

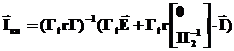
Подставляем в первую формулу:

Перемножим:

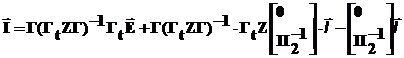
Введем обозначения

у_Е = Г(Г_tzГ)^-1Г_t - матрица входных и взаимных проводимостей

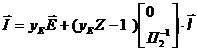
Перед источниками тока стоит коэффициент распределения

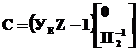
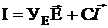
Полученное выражение непосредственно из электрической схемы получить нельзя. Для его получения необходимо громоздкие математические выражения.

К расчету напряжений ветвей электрической схемы:

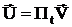из метода условных напряжений

Запишем узловое уравнение:

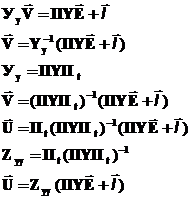
Непосредственно из электрической схемы выражение для напряжений получить нельзя. Для его получения необходимо провести много математических вычислений.

В электрических расчетах применяется матрица узловых сопротивлений