Классическая модель линейной регрессии
Лабораторная работа 1
Классическая модель линейной регрессии
Задания:
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов по данным о деятельности крупнейших компаний США в 2012 г.
2. Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.
3. Постройте модель с информативными факторами.
4. Оцените с помощью F-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи.
5. Оцените статистическую значимость коэффициентов регрессии с помощью t- критерия Стьюдента.
6. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
7. Оцените качество уравнения через среднюю ошибку аппроксимации.
8. Постройте модель в стандартизованном масштабе и проинтерпретируйте ее параметры.
9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.
10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 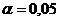 .
.
11. По полученным результатам сделайте экономический вывод.
Реализация типовых заданий:
Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.
Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии.
Парные коэффициенты корреляции рассчитываются по формулам:
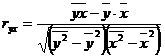 ;
; 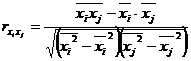 .
.
Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:
1) в главном меню последовательно выберите пункты Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;
2) заполнит диалоговое окно ввода данных и параметров вывода (рисунок 3);
3) результаты вычислений – матрица коэффициентов парной корреляции – представлены на рисунке 4.
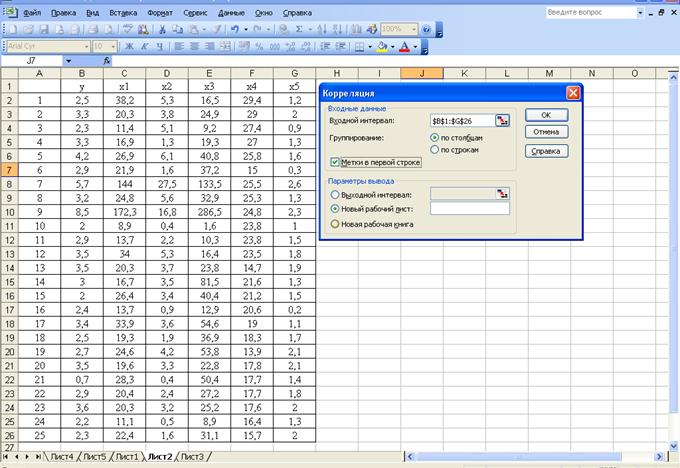
Рисунок 3 - Диалоговое окно ввода параметров инструмента Корреляция
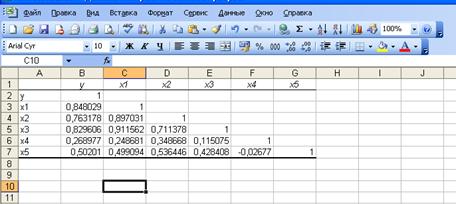
Рисунок 4 – Матрица коэффициентов парной корреляции
Из матрицы можно заметить, что факторы 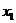 и
и 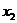 ,
, 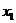 и
и 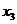 мультиколлинеарны, т.к. коэффициенты корреляции превышают 0,75. Таким образом, можно сказать, что они дублируют друг друга.
мультиколлинеарны, т.к. коэффициенты корреляции превышают 0,75. Таким образом, можно сказать, что они дублируют друг друга.
При отборе факторов в модель предпочтение отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В нашем примере получаем, информативными факторами являются: 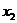 и
и 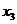 .
.
Построим новое уравнение множественной регрессии с информативными факторами.
Лабораторная работа 2
Системы линейных одновременных уравнений
Задания
1)построить модель вида, 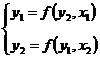 рассчитав соответствующие структурные коэффициенты. Исходные данные представлены в таблице 8.23.
рассчитав соответствующие структурные коэффициенты. Исходные данные представлены в таблице 8.23.
2)оценить параметры модели –I Клейна, используя данные таблицы 8.24.

где 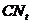 - потребление;
- потребление;
 - текущий и лаговый незарплатный доход (прибыль), долл. США;
- текущий и лаговый незарплатный доход (прибыль), долл. США;
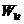 - заработная плата работников занятых в частном секторе, долл. США;
- заработная плата работников занятых в частном секторе, долл. США;
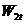 - заработная плата работников занятых в государственном секторе, долл. США;
- заработная плата работников занятых в государственном секторе, долл. США;
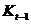 - запас капитала на начало года, долл. США;
- запас капитала на начало года, долл. США;
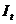 - чистые инвестиции, долл. США;
- чистые инвестиции, долл. США;
 - текущий и лаговый частный продукт (равен НД + косвенные налоги на бизнес -
- текущий и лаговый частный продукт (равен НД + косвенные налоги на бизнес - 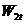 );
);
Реализация типовых заданий
1Построить модель вида, 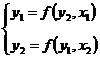 рассчитав соответствующие структурные коэффициенты.
рассчитав соответствующие структурные коэффициенты.
Составим систему структурных уравнений:
 .
.
Для выбора метода оценки параметров проверим систему на идентифицированность.
Таблица 8.23 – Исходные данные для построения системы взаимозависимых уравнений
| Годы | Годовое потребление свинины на душу населения, кг | Оптовая цена за 1 кг свинины, р. | Доход на душу населения, р. | Расходы по обработке мяса, % к цене |
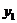 | 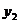 | 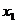 | 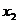 | |
| 5,0 | ||||
| 4,0 | ||||
| 4,2 | ||||
| 5,0 | ||||
| 3,8 | ||||
| Итого | 22,0 |
Необходимое условие:
В модели 2 предопределенные переменные: 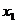 ,
, 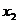 и такое же количество эндогенных переменных:
и такое же количество эндогенных переменных: 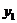 и
и 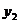 . Следовательно, М=2 и К=2.
. Следовательно, М=2 и К=2.
Проверим необходимое условие для каждого уравнения системы.
Для первого уравнения:
k1=2; m1=1
M-m1=1=k-1=1 следовательно, уравнение точно идентифицировано.
Для второго уравнения:
k2=2; m2=1
M-m2=1=k-1=1 следовательно, уравнение точно идентифицировано.
Так как оба уравнения точно идентифицированы, система в целом тоже точно идентифицирована.
Достаточное условие:
Для того чтобы уравнение было точно идентифицируемым, достаточно чтобы ранг матрицы А (матрица коэффициентов при переменных, не входящих в данное уравнение) был равен (К-1).
Так в нашем примере система состоит только из двух уравнений, то данное условие не проверяется.
Для определения параметров точно идентифицированной модели применяется КМНК.
На первом этапе структурную форму преобразуем в приведенную форму:
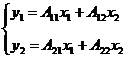 .
.
Параметры модели А11, А12, А21, А22 определяются с помощью традиционного МНК. Найдем данные параметры используя функцию Excel Сервис– Анализ данных– Регрессия (при этом необходимо учесть, что в уравнениях отсутствует свободный член). Результаты регрессионного анализа приведенной формы представлены на рисунке 8.42.
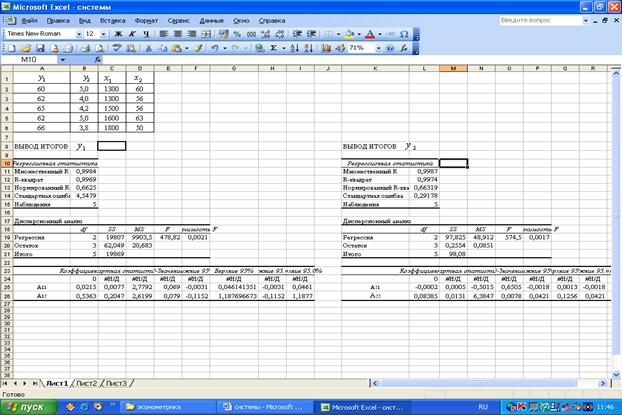
Рисунок 8.42 – Результаты регрессионного анализа уравнений приведенной формы
Следовательно, приведенная форма примет вид:
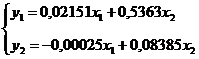 .
.
На следующем этапе определим коэффициенты структурной модели.
В первом уравнении структурной формы в правой части присутствуют переменные 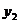 и
и 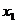 . Следовательно, необходимо из второго уравнения выразить переменную
. Следовательно, необходимо из второго уравнения выразить переменную 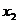 через переменные
через переменные 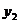 и
и 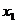 . Получим:
. Получим: 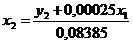 . Подставим полученное выражение в первое уравнение и приведем подобные слагаемые:
. Подставим полученное выражение в первое уравнение и приведем подобные слагаемые: 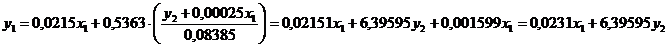
Во втором уравнении структурной формы в правой части присутствуют переменные 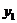 и
и 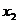 . Следовательно, необходимо из первого уравнения выразить переменную
. Следовательно, необходимо из первого уравнения выразить переменную 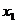 через переменные
через переменные 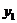 и
и 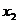 . Получим:
. Получим: 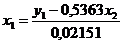 . Подставим полученное выражение в первое уравнение и приведем подобные слагаемые:
. Подставим полученное выражение в первое уравнение и приведем подобные слагаемые: 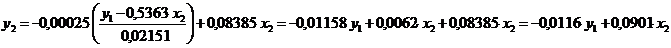 Таким образом, структурная форма модели примет вид:
Таким образом, структурная форма модели примет вид:
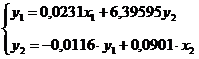 .
.
Рассчитаем по полученным уравнениям теоретические значения 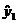 и
и 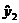 . Результаты расчетов представлены на рисунке 8.43.
. Результаты расчетов представлены на рисунке 8.43.
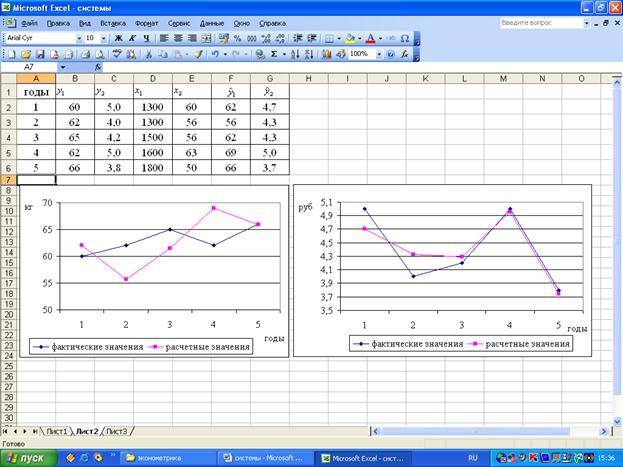
Рисунок 8.43 – Фактические и расчетные значения переменных 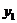 и
и 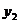
ПриложениеЕ
(обязательное)
Варианты заданий
Вариант 1
Модель денежного рынка:
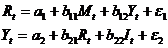 ,
,
где R- процентная ставка;
Y – ВВП;
М – денежная масса;
I – внутренние инвестиции;
t– текущий период.
Вариант 2
Модель Менгеса:

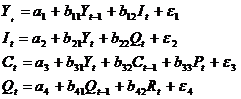 ,
,
где Y – национальный доход;
С – расходы на личное потребление;
I – чистые инвестиции;
Q – валовая прибыль экономики;
Р – индекс потребительских цен;
R– объем продукции промышленности;
t– текущий период;
t-1 – предыдущий период.
Вариант 3
Макроэкономическая модель экономики (одна из версий):
 (функция потребления),
(функция потребления),
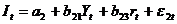 (функция инвестиций),
(функция инвестиций),
 (функция денежного рынка),
(функция денежного рынка),
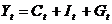 (тождество дохода),
(тождество дохода),
гдеС – расходы на потребление;
Y – ВВП;
I – инвестиции;
R – процентная ставка;
М – денежная масса;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 4
Одна из версий модифицированной модели Кейнса имеет вид:
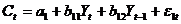 ,
,
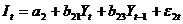 ,
,
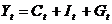 ,
,
гдеС – расходы на потребление;
Y – ВВП;
I – инвестиции;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 5
Модель мультипликатора-акселератора:


 ,
,
гдеС – расходы на потребление;
I – инвестиции;
R – процентная ставка;
t – текущий расход;
t-1 – предыдущий период.
Вариант 6
Одна из версий модели Кейнса имеет вид:
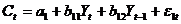 ,
,
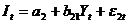 ,
,
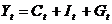 ,
,
гдеС – расходы на потребление;
Y – ВВП;
I – инвестиции;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 7
Модифицированная модель Кейнса имеет вид:
 ,
,
 ,
,
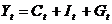 ,
,
гдеС – расходы на потребление;
Y – ВВП;
I – инвестиции;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 8
Гипотетическая модель экономики:
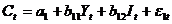 ,
,
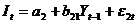 ,
,
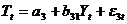 ,
,
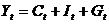 ,
,
гдеС – совокупное потребление;
Y – совокупный доход;
I– инвестиции;
T – налоги;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 9
Модель денежного рынка:
 ,
,
 ,
,
 ,
,
где Y – ВВП;
I – внутренние инвестиции;
R – процентная ставка;
М – денежная масса;
t – текущий расход;
t-1 – предыдущий период.
Вариант 10
Имеется следующая модель кейнсианского типа:
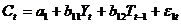 (функция потребления),
(функция потребления),
 (функция инвестиций),
(функция инвестиций),
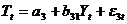 (функция денежного рынка),
(функция денежного рынка),
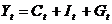 (тождество дохода),
(тождество дохода),
гдеС – совокупное потребление;
Y – совокупный доход;
I – инвестиции;
T– налоги;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 11
Макроэкономическая модель экономики (одна из версий):
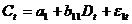 ,
,
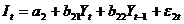 ,
,
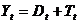 ,
,
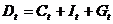 ,
,
гдеС – расходы на потребление;
Y – чистый национальный продукт;
I – инвестиции;
D – чистый национальный доход;
G – государственные расходы;
T– налоги;
t – текущий расход;
t-1 – предыдущий период.
Вариант 12
Упрощенная версия модели Клейна:
 ,
,
 ,
,
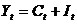 ,
,
гдеС – совокупное потребление;
Y – совокупный доход;
I – инвестиции;
T– налоги;
К – запас капитала;
t – текущий расход;
t-1 – предыдущий период.
Вариант 13
Модель денежного и товарного рынков:
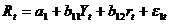 (функция товарного рынка),
(функция товарного рынка),
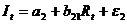 (функция инвестиций),
(функция инвестиций),
 (функция денежного рынка),
(функция денежного рынка),
где R – процентные ставки;
М – денежная масса;
Y – реальный ВВП;
I – внутренние инвестиции;
G – реальные государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 14
Макроэкономическая модель экономики России (одна из версий):
 (функция потребления),
(функция потребления),
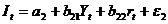 (функция инвестиций),
(функция инвестиций),
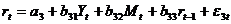 (функция денежного рынка),
(функция денежного рынка),
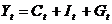 (тождество дохода),
(тождество дохода),
гдеС – совокупное потребление;
Y – ВВП;
I – инвестиции;
r– процентная ставка;
М – денежная масса;
G – государственные расходы;
t – текущий расход;
t-1 – предыдущий период.
Вариант 15
Имеется следующая структурная форма модели:
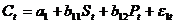 ,
,
 ,
,
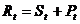 ,
,
гдеС – личное потребление;
S – заработная плата;
P – прибыль;
R – национальный доход;
t – текущий расход;
t-1 – предыдущий период.
ПриложениеЖ
(обязательное)
Исходные данные для выполнения лабораторной работы №6
Таблица Ж.1 – Динамика некоторых макроэкономических показателей РФ
| Текущий период | Валовой внутренний продукт в текущих ценах, млрд. р., до 1998 г. - трлн. р. | Валовой национальный доход (в текущих ценах; млн. р., до 1998г – млрд. р.) | Расходы на конечное потребление (в текущих ценах; млн. р., до 1998г – млрд. р.) | Налоги на производство и импорт (в текущих ценах; млн. р., до 1998г – млрд. р.) | Валовая прибыль экономики и валовые смешанные доходы (в текущих ценах; млн. р., до 1998г – млрд. р.) | Валовое накопление основного капитала (в текущих ценах; млн. р., до 1998г – млрд. р.) | Расходы на конечное потребление государственного управления (в текущих ценах; млн. р., до 1998г – млрд. р.) |
| t | Y | Y | C | T | Q | K | G |
| 1428,5 | 1412717,60 | 1016594,30 | 252401,30 | 610792,00 | 301117,40 | 272501,50 | |
| 2007,8 | 1978923,80 | 1435869,80 | 378712,00 | 699367,00 | 401613,90 | 391381,30 | |
| 2342,5 | 2292045,60 | 1776137,60 | 469958,60 | 783343,70 | 428522,10 | 493573,50 | |
| 2629,6 | 2514429,40 | 2003790,10 | 517923,00 | 946688,50 | 424656,50 | 492620,60 | |
| 4823,2 | 4631958,10 | 3285678,10 | 883308,10 | 2131512,00 | 693958,50 | 703209,10 |

Продолжение таблицы Ж.1
| t | Y | Y | C | T | Q | K | G |
| 7305,6 | 7116553,30 | 4476850,90 | 1404111,50 | 3119932,40 | 1232043,10 | 1102497,10 | |
| 8943,6 | 8819938,90 | 5886860,60 | 1585833,10 | 3692601,40 | 1689315,00 | 1469957,60 | |
| 10830,5 | 10612526,70 | 7484115,50 | 2028443,00 | 3906867,90 | 1939314,40 | 1942441,80 | |
| 13208,2 | 12806796,70 | 9058687,60 | 2318223,00 | 4864328,30 | 2432252,00 | 2366368,70 | |
| 17027,2 | 16658960,30 | 11477849,60 | 3079045,60 | 6306703,70 | 3130523,60 | 2889814,50 | |
| 21609,8 | 21070760,40 | 14438149,20 | 4410767,10 | 7887139,40 | 3836895,90 | 3645918,50 | |
| 26917,2 | 26120717,00 | 17809740,70 | 5542275,30 | 9544584,30 | 4980573,30 | 4680409,70 | |
| 33247,5 | 32463957,80 | 21968579,50 | 6564455,70 | 11387081,60 | 6980359,10 | 5750964,10 | |
| 41276,8 | 40066446,20 | 27543509,10 | 8498539,10 | 13498666,00 | 9200768,90 | 7359844,20 | |
| 38807,2 | 37546122,20 | 29269625,10 | 6808387,90 | 11921085,70 | 8535671,50 | 8066692,60 | |
| 46308,5 | 44830692,90 | 32514673,20 | 8494621,80 | 15093737,80 | 10014340,10 | 8671323,70 | |
| 55967,2 | 54037351,20 | 37439339,50 | 11194306,40 | 17273066,10 | 12075765,00 | 10040761,60 | |
| 62218,4 | 60538893,20 | 42471530,40 | 12745141,10 | 18611642,70 | 13768006,20 | 11664781,30 |
 |
Продолжение таблицы Ж.1
| Текущий период | Инвестиции в текущие цены, млрд. (трлн.) р. | Средняя номинальная заработная плата рублей в месяц | Денежная масса млрд. (трлн.) р. | Доля импорта в ВВП, % | Индекс потребительских цен, в % к предыдущему периоду | Индексы производства по видам экономической деятельности Российской Федерации (в % к предыдущему году) | Средняя ставка рефинансирования, % |
| t | I | S | M | M | P | R | R |
| 472,4 | 213,9 | 4,26 | 95,4 | ||||
| 790,2 | 288,3 | 3,43 | 92,4 | ||||
| 408,8 | 950,2 | 374,1 | 3,15 | 34,2 | |||
| 407,1 | 448,3 | 2,27 | 184,4 | 95,2 | 57,2 | ||
| 670,4 | 704,7 | 0,82 | 136,5 | 108,9 | |||
| 1165,2 | 1144,3 | 0,61 | 120,2 | 108,7 | 39,8 | ||
| 1504,7 | 1602,6 | 0,6 | 118,6 | 102,9 | |||
| 1762,4 | 2119,6 | 0,56 | 115,1 | 103,1 | |||
| 2186,4 | 3212,7 | 0,58 | 108,9 | 19,5 | |||
| 4363,3 | 0,57 | 111,7 | |||||
| 3611,1 | 6045,6 | 0,57 | 110,9 | 105,1 |

Продолжение таблицы Ж.1
| t | I | S | M | M | P | R | R |
| 8995,8 | 0,61 | 106,3 | 11,3 | ||||
| 6716,2 | 13272,1 | 0,67 | 111,9 | 106,8 | 10,5 | ||
| 8781,6 | 13493,2 | 0,7 | 113,3 | 100,6 | 10,8 | ||
| 15697,7 | 0,47 | 108,8 | 90,7 | ||||
| 9151,1 | 20173,5 | 0,53 | 108,8 | 107,3 | 8,4 | ||
| 11035,7 | 24543,4 | 0,57 | 106,1 | ||||
| 12568,8 | 27405,4 | 0,54 | 106,6 | 103,4 | 8,1 |
Лабораторная работа 1
Классическая модель линейной регрессии
Задания:
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов по данным о деятельности крупнейших компаний США в 2012 г.
2. Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.
3. Постройте модель с информативными факторами.
4. Оцените с помощью F-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи.
5. Оцените статистическую значимость коэффициентов регрессии с помощью t- критерия Стьюдента.
6. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
7. Оцените качество уравнения через среднюю ошибку аппроксимации.
8. Постройте модель в стандартизованном масштабе и проинтерпретируйте ее параметры.
9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.
10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 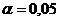 .
.
11. По полученным результатам сделайте экономический вывод.
Реализация типовых заданий:
