Типовые входные воздействия и характеристики звеньев.

Воздействие и их виды.

Как отмечалось выше, САР имеет место управляющие (задающие) и возмущающие воздействия, в результате действия которых в системе возникает переходной процесс, приводящий систему к новому установившемуся состоянию. В реальных условиях воздействия могут иметь произвольный характер. Для исследования динамических свойств элементов и систем выбирают такие типовые воздействия, которые по возможности близко отражали бы наиболее существенные особенности реальных воздействий. Такими воздействиями могут быть либо наиболее вероятные, либо наиболее неблагоприятные воздействия. Причем их можно разделить на регулярные и случайные, непрерывные и дискретные.

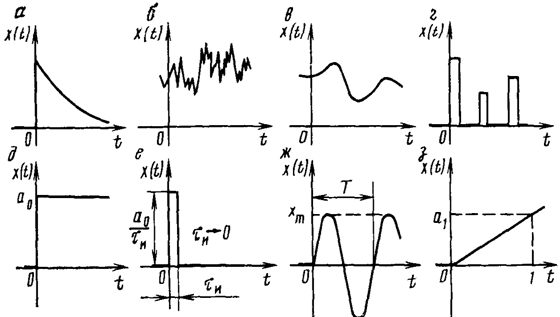
Для анализа выбраны типовые воздействия наиболее полно и иллюстративно показывающие особенности выбранных звеньев. В качестве типовых приняты ступенчатое, гармоническое, линейно возрастающее.

Единичный скачок может возникнуть при мгновенном замыкании или размыкании сети постоянного тока, вызванном приложением или сбросом нагрузки.

Единичное ступенчатое воздействие

.

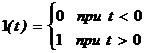Единичное импульсное воздействие

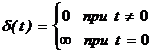так, что .

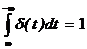Гармоническим воздействием называют функцию, изменяющуюся по закону синуса или косинуса. Оно используется при анализе динамических свойств САР частотными методами. Частотный метод заключается в построении частотных характеристик.

x(t) = 1(t) x_m sin wt.

Для следящих и программных систем типовым является линейное воздействие

x(t) = 1(t) at.

Режимы перехода САУ из одного состояния к другому показанына рисунке.

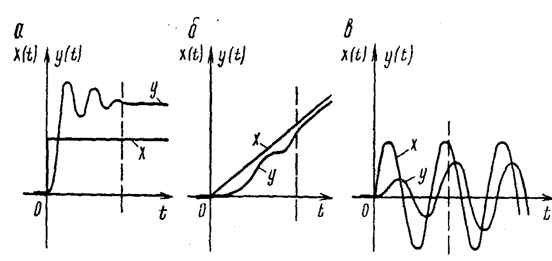
Временные характеристики

Наглядное представление о свойствах звена дает функция, являющаяся решением дифференциального уравнения. Но одно и то же дифуравнение может иметь множество решений, конкретный вид которых зависит от начальных условий и от характера функции, задающей воздействие. Поэтому принято динамические свойства элементов систем характеризовать решением, соответствующим нулевым начальным условиям и одному из типовых воздействий, рассмотренных выше. Наиболее наглядное представление о динамических свойствах элемента дает его переходная характеристика.

Переходной характеристикой h(t) называют изменение выходной величины, возникающее после подачи на вход скачкообразного изменения входной величины при нулевых начальных условиях.

Импульсной переходной характеристикой w(t) называют изменение выходной величины, возникающее после подачи на вход дельта-функции при нулевых начальных условиях.

Импульсная переходная характеристика равна производной от переходной характеристики

w(t) = dh(t)/dt,

и наоборот, переходная характеристика равна интегралу от импульсной переходной характеристики.

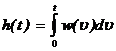
Переходные характеристики и называют также временными.

Частотные характеристики

Частотными характеристиками называются зависимости, связывающие входную и выходную величины линейной системы в установившемся режиме, когда входное воздействие изменяется по гармоническому закону x(t) = a sin wt с частотой и постоянной амплитудой a. На выходе системы после завершения переходного процесса устанавливается синусоидальные колебания y(t) = b sin(wt + j) . На комплексной плоскости входная и выходная величин для каждого момента времени t определены векторами а и b.

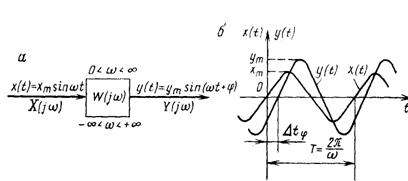
В комплексной тригонометрической форме

x = a(cos wt + j sin wt)

y = b[cos(wt + j) + j sin(wt + j)].

Используя формулу Эйлера e^jwt = cos wt + j sin wt, получим

x(t) = ae^jwt; y(t) = be^j(wt+j).

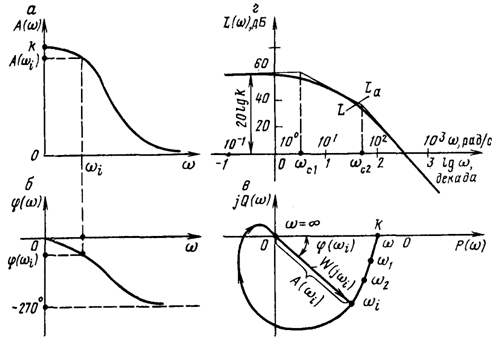
Если амплитуду колебаний входной величины оставить неизменной, а изменять частоту w от нуля до ¥, то каждому значению частоты будут соответствовать определенные значения амплитуды колебаний b и сдвига фазы j на выходе системы. Это значит, что отношение амплитуд и разность фаз являются функциями частоты, т.е:

b/a = A(w); j = j(w).

Рассмотренные выше временные, передаточные и частотные характеристики однозначно связаны меду собой прямым и обратным преобразованиями Лапласа и Фурье. Это отражено в таблице.

Таблица.

Взаимные соответствия динамических характеристик.

Характер-ки	h(t)	w(t)	W(p)	W(jw)
Переходная h(t)=		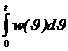	L-1{W(p)/p}	F-1{W(jw)/ jw}
Импульсная w(t)=	dh(t)/dt		L-1{W(p)}	F-1{W(jw)}
Передаточная W(p)=	pL{h(t)}	L{w(t)}		W(jw)½p=jw
Частотная W(jw)=	jwF{h(t)}	F{w(t)}	W(p)½p=jw