Интегралы. диффернциальные уравнения

Задача 1. Найти неопределенные интегралы.

1.1.	а)		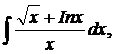б)		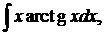в)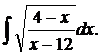
1.2.	а)		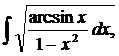б)		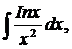в)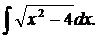
1.3.	а)		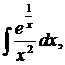б)		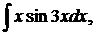в)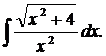
1.4.	а)		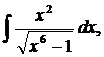б)		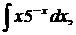в)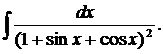
1.5.	а)		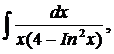б)		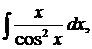в)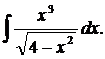
1.6.	а)		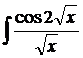б)		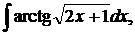в)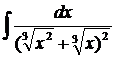
1.7.	а)		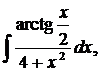б)		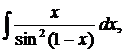в)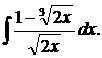
1.8.	а)		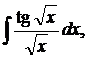б)		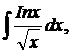в)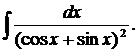
1.9.	а)		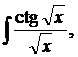б)		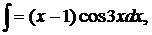в)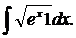
1.10.	а)		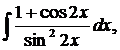б)		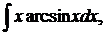в)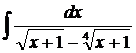
1.11.	а)		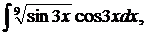б)		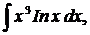в)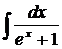
1.12.	а)		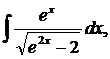б)		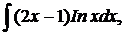в)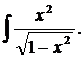
1.13.	а)		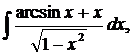б)		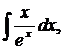в)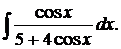
1.14.	а)		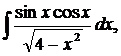б)		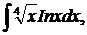в)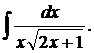
1.15.	а)		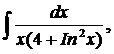б)		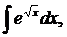в)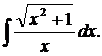
1.16.	а)		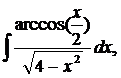б)		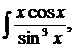в)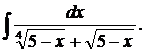
1.17.	а)		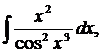б)		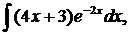в)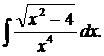
1.18.	а)		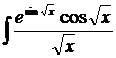б)		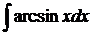в)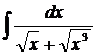
1.19.	а)		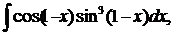б)		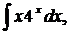в)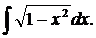
1.20.	а)		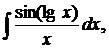б)		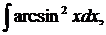в)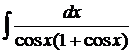
1.21.	а)		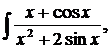б)		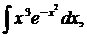в)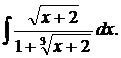
1.22.	а)		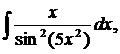б)		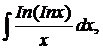в)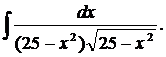
1.23.	а)		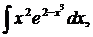б)		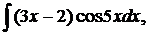в)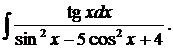
1.24.	а)		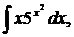б)		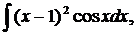в)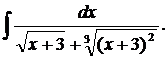
1.25.	а)		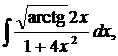б)		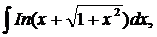в)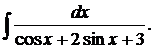
1.26.	а)		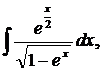б)		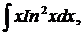в)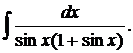
1.27.	а)		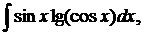б)		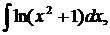в)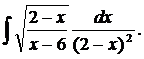
1.28.	а)		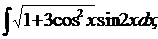б)		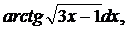в)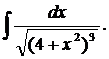
1.29.	а)		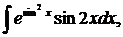б)		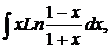в)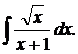
1.30.	а)		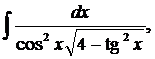б)		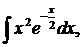в)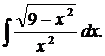

Задача 2.В данном задании необходимо решить 2 задачи. Номер варианта определяется цифрами, стоящими в скобках.

Вычислить площадь плоской фигуры, ограниченной линиями, заданными уравнениями в декартовых координатах.

(01)		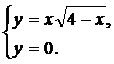(04)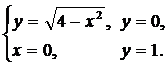
(11)		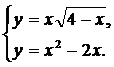(15)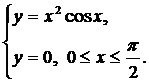
(20)		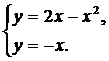(25)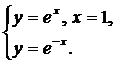
(29)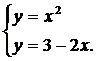

Вычислить площадь плоской фигуры, ограниченной линиями, заданными уравнениями в полярных координатах.

(02)		(06)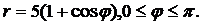
(12)		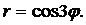(16)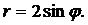
(19)		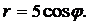(23)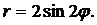
(27)		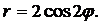(30)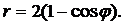

Вычислить площадь плоской фигуры, ограниченной линиями, заданными параметрически.

(03)		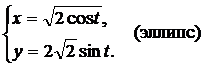(08)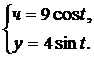
(10)		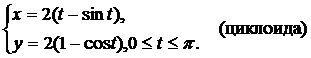(13)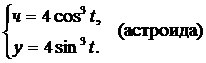
(18)		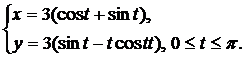(21)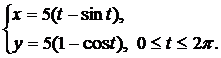
(24)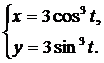

Вычислить длину дуги кривой, заданной уравнением в декартовой системе координат.

(02)
(06)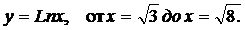
(10)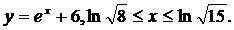
(13)
(18)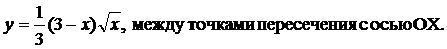
(23)

Вычислить длину дуги кривой, заданной уравнением в полярных координатах.

(04)		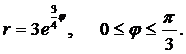(07)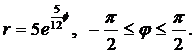
(09)		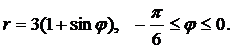(14)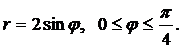
(17)		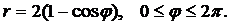(22)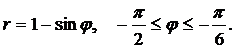
(26)		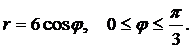(29)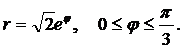

Вычислить длину дуги кривой, заданной параметрически.

(01)		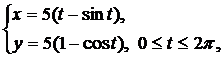(05)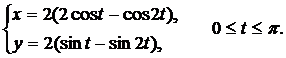
(11)		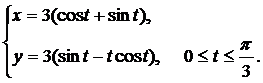(15)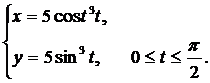
(20)		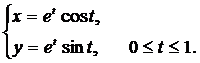(25)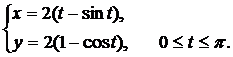
(28)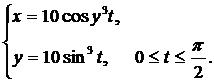

Вычислить объемы тел, полученных вращением вокруг оси ОХ плоской фигуры, ограниченной линиями, заданными в декартовых координатах.

(02)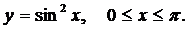
(07)		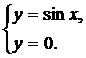(09)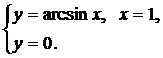
(14)		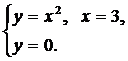(17)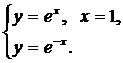
(21)		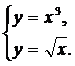(24)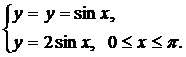
(27)		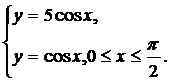(30)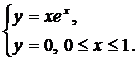

Вокруг оси ОY.

(05)		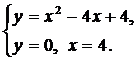(08)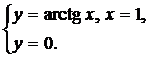
(12)		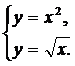(16)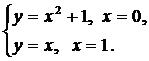
(19)		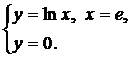(22)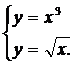
(26)		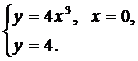(28)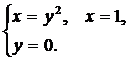

Задача 4. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию.

4.1.	.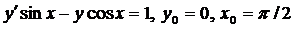
4.2.	.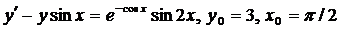
4.3.	.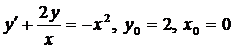
4.4.	.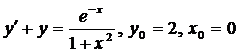
4.5.	.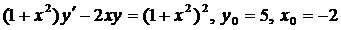
4.6.	.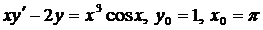
4.7.	.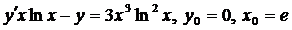
4.8.	.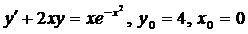
4.9.	.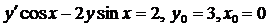
4.10.	.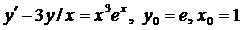
4.11.	.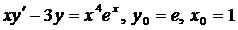
4.12.	.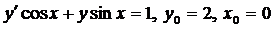
4.13.	.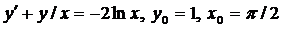
4.14.	.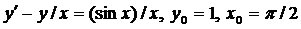
4.15.	.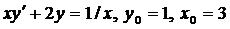
4.16.	.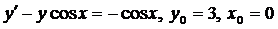
4.17.	.
4.18.	.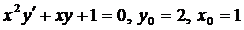
4.19.	.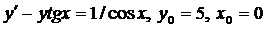
4.20.	.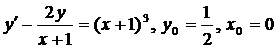
4.21.	.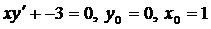
4.22.	.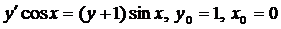
4.23.	.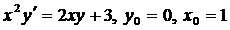
4.24.	.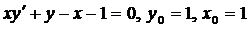
4.25.	.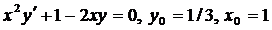
4.26.	.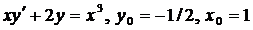
4.27.	.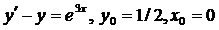
4.28.	.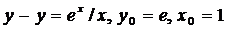
4.29.	.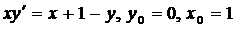
4.30.	.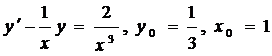
4.31.	.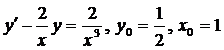

Задача 5. Найти общее решение дифференциального уравнения, допускающего понижение порядка.

5.1.	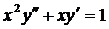.	5.2.	.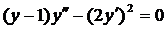
5.3.	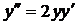.	5.4.	.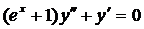
5.5.	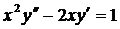.	5.6.	.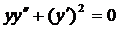
5.7.	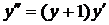.	5.8.	.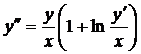
5.9.	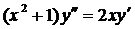.	5.10.	.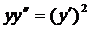
5.11.	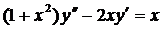.	5.12.	.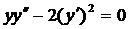
5.13.	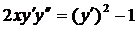.	5.14.	.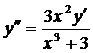
5.15.	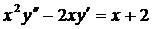.	5.16.	.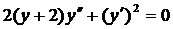
5.17.	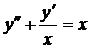.	5.18.	.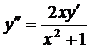
5.19.	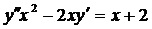.	5.20.	.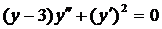
5.21.	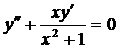.	5.22.	.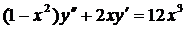
5.23.	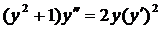.	5.24.	.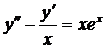
5.25.	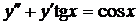.	5.26.	.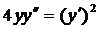
5.27.	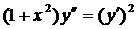.	5.28.	.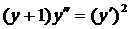
5.29.	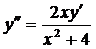.	5.30.	.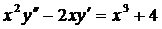

Задача 6. Найти общее решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами с правой частью специального вида.

6.1.	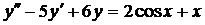.	6.2.	.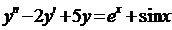
6.3.	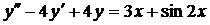.	6.4.	.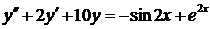
6.5.	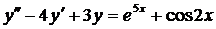.	6.6.	.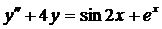
6.7.	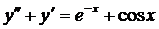.	6.8.	.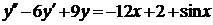
6.9.	.	6.10.	.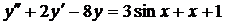
6.11.	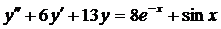.	6.12.	.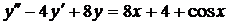
6.13.	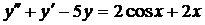.	6.14.	.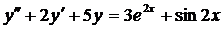
6.15.	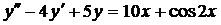.	6.16.	.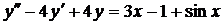
6.17.	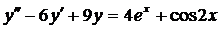.	6.18.	.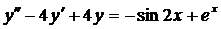
6.19.	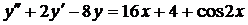.	6.20.	.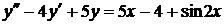
6.21.	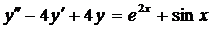.	6.22.	.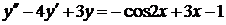
6.23.	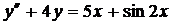.	6.24.	.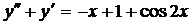
6.25.	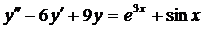.	6.26.	.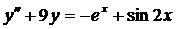
6.27.	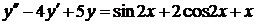.	6.28.	.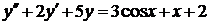
6.29.	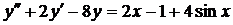.	6.30.	.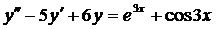

Список литературы

1. Пискунов Н. С.Дифференциальное и интегральное исчисления. – М.: Наука. Т. 1,2.

2. Бугров Я. С., Никольский С. М.Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука.

3. Задачи и упражнения по математическому анализу для втузов/ Под редакцией Демидовича В. П.– М.: Наука.

4. Данко П. Е., Попов А. Г., Кожевникова Т. Я.Высшая математика в упражнениях и задачах. – М.: Высшая школа. Ч. 1,2.

5. Сборник задач по математике для втузов/ Под редакцией Ефимова А. В., Демидовича В. П.– М.: Наука.