Векторные функции скалярного аргумента
Если каждому значению скалярного аргумента t поставить в соответствие вектор r(t), то r(t)называетсявекторной функцией (вектор-функцией)скалярного аргумента t.
 |
Рис. 3.11
Если начало вектора r(t) (радиус-вектора) поместить в постоянную точку О, то конец радиус-вектора r(t)опишет пространственную кривую, которую называют годографом векторнойфункции (см. рис. 3.11).
Если t означает время, то r(t)описывает траекторию движения материальной точки. Если r(t)разложить по базисным векторам i, j, k прямоугольной декартовой системы координат, то
,
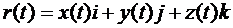причем компоненты x(t), y(t), z(t)являются функциями от t. Параметрическое представление пространственной кривой (годографа) или траектории движения имеет вид
x = x(t), y = y(t), z = z(t).
Предел и непрерывность
Если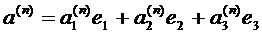 
( 
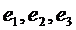- базис )-последовательность векторов, то вектор 
называется предельным вектором этой последовательности (обозначается 
),
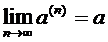если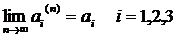 
.
Вектор называется пределом векторной функции
при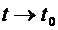 
( обозначается 
) если 
.Это равнозначно тому, что 
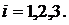В частности, r(t)называется непрерывной в точке t0, если 
, что эквивалентно непрерывности компонент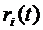 
в точке t0.
Дифференцирование векторной функции
Если существует предел
,
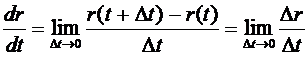то 
называется производной от r(t)в точке t.(cм. Рис. 3. 12)
 |
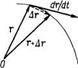Рис. 3.12.
В другой записи: r'(t)или 
. В декартовой системе координат: 
Вектор r'(t)имеет направление касательной к годографу в точке t и направлен в сторону, отвечающую возрастанию параметра t. Длина r'(t) зависит от выбора параметра t. Если t есть длина дуги, то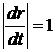 
.
Если t означает время, а r(t)— траекторию движения материальной точки, то r'(t) —вектор скорости, | r' (t)| — величина скорости.
Правила дифференцирования
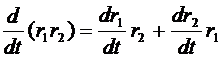
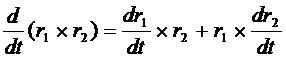(множители нельзя менять местами)
Если r(t) — единичный вектор, то годограф лежит на единичной сфере и касательная всегда перпендикулярна радиус-вектору, т. е.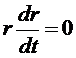 
.
Производные высших порядков
Рассматривая r'(t)при переменном t как векторную функцию, производную от r'(t) обозначают через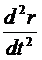 
, или r"(t), или 
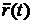. В декартовых координатах:
.
Если r(t)описывает движение материальной точки, то r" (t)— вектор ускорения,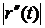 
- величина ускорения. Аналогично определяются третья, четвертая, п-я производные.
Разложение по формуле Тейлора имеет вид:
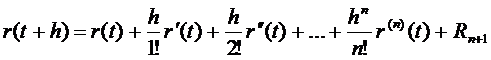
Это ни что иное, как векторная сумма разложений по формуле Тейлора для функций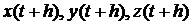 
, 
остаточный член.
Дифференциал функции r (t) определяется формулой
Кривизна кривой
Кривизной К кривой в ее точке М называется предел отношения угла между положительными направлениями касательных в точкай М и N кривой (угол смежности) к длине дуги 
, когда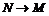 
, т.е.
, где
|
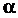- угол между положительными направлениями касательной в точке М и оси Ох.
Радиусом кривизны R называется величина, обратная абсолютной величине кривизны, т.е.
.
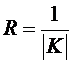Формула для вычисления кривизны в прямоугольных координатах ( с точностью до знака)
имеет вид
.
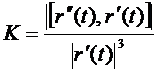В случае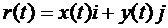 
.
Задача
Векторная функция 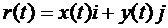задает траекторию движения точки.
1. Построить годограф векторной функции.
2. Вычислить координаты вектора скорости и ускорения в точке t=t1.
3. Найти кривизну траектории в произвольной точке и вычислить радиус кривизны в точке t=t1.
Решение.
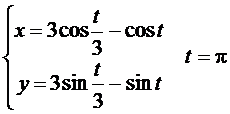
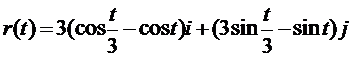
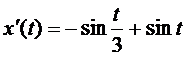
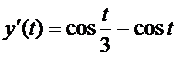
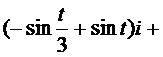
- вектор скорости
+ 
= 
= 
= 
+ 
=
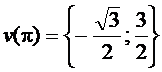
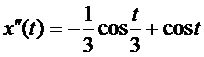
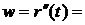
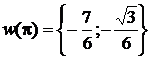
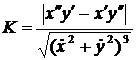
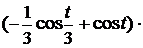
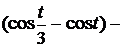
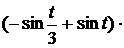
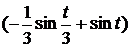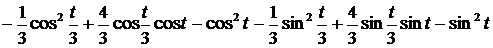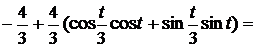
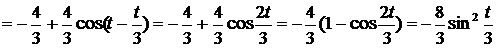
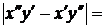
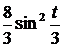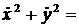
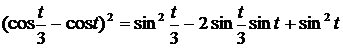
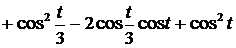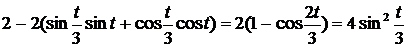
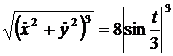
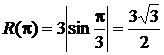
Приложения производной
Прежде чем перейти к наиболее важным приложениям производной при исследовании функций и построении их графиков, рассмотрим несколько основных теорем.