Дифференцируемость функции в точке
Определение 3.2. Функция 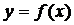 называется дифференцируемой в точке
называется дифференцируемой в точке 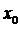 , если ее приращение
, если ее приращение 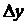 в этой точке можно представить в виде
в этой точке можно представить в виде
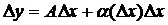 , (3.4)
, (3.4)
где  - некоторое число, не зависящее от
- некоторое число, не зависящее от 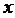 , а
, а  - функция аргумента
- функция аргумента  , являющаяся бесконечно малой при
, являющаяся бесконечно малой при  , т.е.
, т.е.  .
.
Равносильность дифференцируемости функции в точке и существования в этой точке конечной производной данной функции устанавливает следующая теорема.
Теорема 3.1. Для дифференцируемости функции 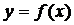 в точке
в точке 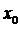 необходимо и достаточно, чтобы она имела в этой точке конечную производную.
необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство. Необходимость. Пусть функция 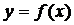 дифференцируема в точке
дифференцируема в точке 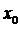 , т.е. ее приращение в этой точке можно представить в виде (3.4). Поделим равенство (3.4) на
, т.е. ее приращение в этой точке можно представить в виде (3.4). Поделим равенство (3.4) на  (при
(при  ), получим
), получим 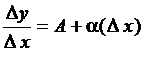 .
.
Переходя к пределу при 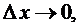 имеем
имеем 
Отсюда следует, что производная в точке 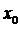 существует и равна A:
существует и равна A: 
Достаточность. Пусть существует конечная производная 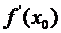 , т.е.
, т.е.  Пусть
Пусть  ; тогда функция
; тогда функция  является бесконечно малой при
является бесконечно малой при 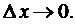
Из последнего равенства имеем  где
где 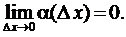 Получено представление (3.4), тем самым доказано, что функция
Получено представление (3.4), тем самым доказано, что функция 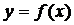 дифференцируема в точке
дифференцируема в точке 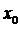 .
.
Таким образом, для функции одной переменной дифференцируемость и существование производной - понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.
Определение 3.3. Функцию, дифференцируемую в каждой точке открытого множества  , называют дифференцируемой на множестве
, называют дифференцируемой на множестве  .
.
Например, функция 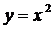 дифференцируема в любой точке множества
дифференцируема в любой точке множества 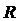 .
.
Пример. Доказать, что функция 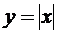 не дифференцируема в точке
не дифференцируема в точке 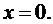
Решение. Производная функции (если она существует) равна  Очевидно, что при
Очевидно, что при  производная не существует, так как отношение
производная не существует, так как отношение 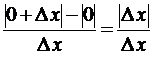 равно 1 при
равно 1 при 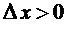 и
и
-1 при 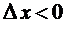 , т.е. не имеет предела при
, т.е. не имеет предела при 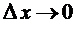 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке
(ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке  (рис. 3.8).
(рис. 3.8).
 |
Рис. 3.8
Следущая теорема устанавливает связь между понятиями дифференцируемости и непрерывности.
Теорема 3.2.Если функция 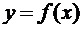 дифференцируема в точке
дифференцируема в точке 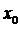 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство. Так как функция 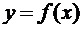 дифференцируема в точке
дифференцируема в точке 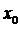 , то ее приращение в этой точке может быть представлено соотношением (3.4). Тогда, переходя к пределу при
, то ее приращение в этой точке может быть представлено соотношением (3.4). Тогда, переходя к пределу при 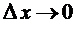 , получаем
, получаем
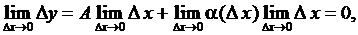 что и означает непрерывность функции
что и означает непрерывность функции 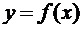 в точке
в точке 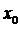 , согласно определению непрерывности функции в точке.
, согласно определению непрерывности функции в точке.
Обратная теорема не верна, т.е. если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Так, функция  непрерывна в точке
непрерывна в точке  , так как
, так как 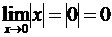 (рис. 3.8), но, как было доказано, не дифференцируема в этой точке.
(рис. 3.8), но, как было доказано, не дифференцируема в этой точке.
Таким образом, непрерывность функции – необходимое, но не достаточное условие дифференцируемости функции.
В математике известны непрерывные функции, но не дифференцируемые ни в одной точке.
Замечание. Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке X, то функция называется гладкой на этом промежутке. Если же производная функции допускает конечное число точек разрыва (причем, первого рода), то такая функция на данном промежутке называется кусочно - гладкой.
