Описание содержания основных тем

Дифференциальное исчисление функции одной переменной.

Определение производной, ее геометрический и механический смысл. Правила дифференцирования. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции. Производные основных элементарных функций. Дифференциал, его геометрический смысл. Производные и дифференциалы высших порядков. Теоремы Ферма, Ролля, Лагранжа. Правило Лопиталя. Формула Тейлора. Исследование функций и построение графиков. Кривизна кривой.

Интегральное исчисление функции одной переменной.

Первообразная. Неопределенный интеграл, его свойства. Таблица интегралов. Замена переменной в неопределенном интеграле интегрирование по частям. Интегрирование рациональных дробей, тригонометрических и иррациональных функций. Определение определенного интеграла. Теоремы существования определенного интеграла. Свойства определенного интеграла. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле, интегрирование по частям. Приложения определенного интеграла.

Дифференциальные уравнения.

Дифференциальные уравнения первого порядка. Задача Коши. Теорема Коши. Уравнения высших порядков. Уравнения, допускающие понижения порядка. Линейные уравнения. Метод вариации произвольных постоянных. Линейные уравнения с постоянными коэффициентами. Системы дифференциальных уравнений.

Опорный конспект лекций

Дифференциальное исчисление.

Производная.

Задачи, приводящие к определению производной

Задача о скорости движения.

Пусть вдоль некоторой прямой движется точка по закону , где - пройденный путь, - время. Необходимо найти скорость точки в момент 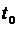, - приращение времени, - приращение расстояния.

К моменту времени 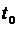пройденный путь равен 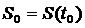, а к моменту - путь 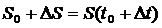(рис. 3.1).

Рис. 3.1

Тогда за промежуток средняя скорость равна . Она зависит от значения : чем меньше , тем точнее выражает скорость движения точки в данный момент времени . Поэтому под скоростью точки в момент понимают предел средней скорости за промежуток от 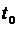до , когда 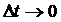, т.е.

.

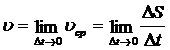Задача о касательной.

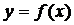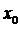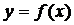Пусть на плоскости дана непрерывная кривая . Необходимо найти уравнение касательной к этой кривой в точке . Дадим аргументу приращение и перейдем на кривой от точки к точке . Проведем секущую (рис. 3.2).

Касательной к кривой 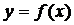в точке называется предельное положение секущей при приближении точки по кривой к точке , т.е. при .

Рис.3.2

Обозначим через 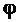угол между секущей и осью ; - угол, образованный касательной с осью . Угловой коэффициент(или тангенс угла 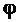наклона) секущей может быть найден из : . Тогда угловой коэффициент касательной

.

Определение производной. Уравнение касательной и нормали

К кривой. Связь между непрерывностью и дифференцируемостью

Функции

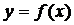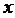Пусть функция определена на промежутке . Возьмем точку . Дадим значению приращение 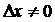, тогда функция получит приращение .

Определение 3.1. Производной функции 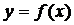называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

. (3.1)

Производная функции имеет несколько обозначений: ; ; ; .

Иногда в обозначении производной используется индекс, указывающий по какой переменной взята производная, например, .

Пример. 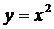. Найти .

Зафиксируем 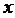. Тогда 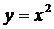. Пусть - приращение аргумента. Тогда . Получаем .

Находим 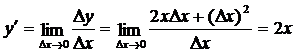, значит, .

Из задачи о касательной вытекает геометрический смысл производной: производная есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой 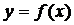в точке 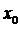, т.е. . Тогда уравнение касательной к кривой 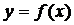в точке 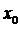примет вид

. (3.2)

Нормалью к кривой в точке 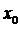называется прямая, перпендикулярная касательной, проходящей через точку 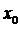, тогда

и уравнение нормали примет вид

(если ). (3.3)

Из задачи о скорости движения следует механический смысл производной: производная пути по времени есть скорость точки в момент :