Энергетический обнаружитель ШПС

При полной априорной неопределенности (несущей частоты, диапазона частот, ширины спектра F ШПС, факта работы ШСС, остальных параметров ШПС) применяют поисковый энергетический приемник-обнаружитель (радиометр), структурная схема которого (без ВЧ части) и рабочие характеристики даны на рис.4.10.

Рис.4.10. Энергетический обнаружитель и его рабочие характеристики. .

Обнаружитель формирует статистику:

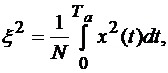(4.40)

которая сравнивается с порогом , зависящем согласно алгоритму Неймана-Пирсона [3] от СПМ ШПС на входе и шумов приемника (РПУ):

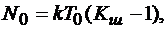(4.41)

где - время анализа, -мощность ШПС, -коэффициент шума приемника, 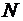-объем выборки по Котельникову на интервале анализа :

(4.42)

Вероятности ложной тревоги и правильного обнаружения (при малом ОСШ на входе обнаружителя и объеме выборки ) равны:

(4.43)

(4.44)

где F – интеграл вероятности [3].

Рабочие характеристики обнаружителя рис.4.10 зависят от параметра 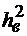обнаружения (ОСШ на выходе обнаружителя, т. е. входе ПУ)

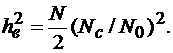(4.45)

При заданном значении параметра 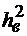из (4.45) с учетом (4.41), (4.42) найдем необходимое время анализа

(4.46)

Время анализа (энергетическая скрытность) увеличивается с ростом ширины спектра ШПС F_с, требуемого ОСШ на выходе обнаружителя и уменьшением ОСШ на входе обнаружителя.

Оптимальный обнаружитель М-ичной ШСС с ШПС.

Если в ШСС используется М известных ШПС с известной в приемнике формой ШПС, то схема оптимального многоканального некогерентного обнаружителя (при малом ОСШ на входе) имеет вид рис.4.11.

Рис.4.11. Оптимальный многоканальный некогерентный обнаружитель ШПС.

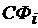- фильтр согласованный с 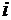-тым ШПС, ; где m=М,

ГФ- гребенчатый фильтр (рециркулятор [П]), настроенный на

частоту повторения ШПС, равную 1/Т; Т- длительность ШПС.

Параметр обнаружения оптимального обнаружителя выражается через одноименный параметр энергетического обнаружителя (4.45):

(4.47)

где база ШПС.

Чем больше база ШПС, тем больше ОСШ на выходе обнаружителя, а увеличение М приводит к повышению скрытности ШСС.

Можно найти аналогично (4.46) время анализа ШПС оптимального обнаружителя

(4.48)

Время анализа не зависит от ширины спектра ШПС, т.к. она в неявном виде входит в импульсную характеристику СФ. Кроме того, время анализа увеличивается с ростом М и при уменьшении длительности Т ШПС, т.е. с уменьшением объема накапливаемой выборки в ГФ и ФНЧ, что приводит к увеличению времени анализа.

Задачи

1. Двоичный ФМ сигнал получен манипуляцией КП Баркера при N=11:

/ 1 1 1-1-1-1 1 -1-1 1-1/.

Вычислить значения АКФ R(μ) КП Баркера при μ = 0, ±1, ±2….±N и построить график.

Исследовать КП Баркера на сбалансированность кода и блоковую структуру КП.

Построить СФ для приема КП Баркера.

Исследовать блоковую структуру СП, вычислить объем ансамбля СП при N=11, сравнить с структурой КП Баркера.

2. Двоичный ФМ сигнал получен манипуляцией М-последовательностью, генерируемой согласно характеристическому полиному

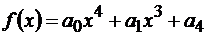с коэффициентами 10011 [1, табл.3.9].

Построить схему генератора ПСП.

Записать 1 период (N=15) ПСП, снимаемой с выхода Т_1.

Вычислить значения АКФ R(μ) ПСП при μ = 0, ±1, ±2….±N и построить график.

Исследовать ПСП (М-последовательность) на сбалансированность кода и соответствие блоковой структуре СП из N=15 элементов. Вычислить число Q типичных СП и сравнить с числом Q_m для M-последовательностей (при k =4 Q_m =2 [1, табл.3.9]).

3. Спроектировать сегментную производную систему сигналов, если в качестве исходной ПСП принять М - последовательность длиной N=4096 символов, а эффективное значение пиков ВКФ производной системы сигналов не должно превышать значение R_ij (τ) =4.

4. Для М-последовательности а(ν), генерируемой с выхода триггера Т₁ согласно характеристическому полиному с коэффициентами /10011/ записать циклическую перестановку а(ν+μ), где μ=5. Взять вторую М-последовательности b(ν) c коэффициентами /11001/ и нарисовать схему реализации генератора ПСП Голда.

5. Даныдве образующие М-последовательности а(ν) и b(ν), генерируемые с выхода триггера Т₁ согласно характеристическим полиномам неприводимых многочленов, заданных коэффициентами соответственно: а(ν) →/1000011/; b(ν) →/1011/.

Алгоритм образования малой циклической системы Кассами:

{C_j(ν)}={А(ν)} {D(j)B(ν)

Записать две реализации ПСП малой системы Касами.

6. Построить матрицы ЧКП композиционной системы ДЧ сигналов согласно алгоритму: , ;

где r =5, 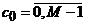, М=7. Объем системы равен L_комп =42, а R_max ≤ 3/7.

7. Радиолокационная станция (РЛС) ведет контроль воздушного пространства при АБГШ с двухсторонней СПМ излучением радиоимпульсов длительностью 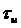на 128 частотах в режиме ППРЧ с тактом переключения частот излучения . В приемнике РЛС реализуется параллельный анализ сигналов на этих частотах (обработкой с уплотнением во времени), т. е. прием отраженного от цели радиоимпульса на СФ с последетекторным накоплением в рециркуляторе (РЦ) импульсов, принятых на частотах ППРЧ. Процессор обработки в РПУ обеспечивает устойчивость РЦ с коэффициентом обратной связи .

Построить СФ с накоплением на РЦ, найти оптимальные параметры РЦ и ОСШ на входе решающей схемы обнаружения цели, полагая шум на выходе детектора АБГШ со СПМ .

8. В задаче по п.7 на каждой из 128 частот вместо радиоимпульсов РЛС излучает КП Баркера длительностью Т= 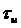·N, где N=11, и тактом переключения частот Т₀ =2Т.

Построить СФ с накоплением на РЦ, найти оптимальные параметры РЦ и ОСШ на входе решающей схемы обнаружения цели, полагая шум на выходе детектора АБГШ со СПМ .

9. В системах радиосвязи с большой скоростью передачи информации, малым ОСШ и ограничениями на большую базу ШПС высокую помехоустойчивость системы можно обеспечить, применяя М-ичные системы сигналов и помехоустойчивое кодирование, например, недвоичные (N, К) блоковые коды Рида-Соломона [2,14], где длина недвоичного КС (количество символов (двоичных групп)) ., а

К - количество информационных символов. Количество исправляемых ошибок .

Найти вероятность ошибки на бит информации и построить графики ее зависимости от ОСШ для М-ичной ЧМ системы связи с М=32 и кодов

РС при k =5 и t =1,2,4,8.

10. В ШСС с сигналами ФМ-2, прямым расширением спектра (ПРС) и кодовым разделением абонентов применены: корректирующий код Голея (23,12) [14], перемежение символов, прием на СФ и реализована база ШПС В=10³. Допустимая вероятность ошибки на символ в ШСС не более 10^-3.

Построить структурную схему ШСС и рассчитать максимально допустимое число l_a активных абонентов в ШСС, полагая статистические свойства суммарной взаимной помехи от мешающих абонентов (ВКФ системы сигналов) в полосе ШСС эквивалентными свойствам АБГШ с СПМ N_п.Что будет, если учесть шумы приемника и увеличить В→∞?

Библиографический список

1. Варакин Л.Е. Системы связи с шумоподобными сигналами / Л.Е.Варакин. – М.: Радио и связь, 1985. – 384 с.

2. Прокис Дж. Цифровая связь./ Прокис Дж., Перевод с английского под ред. Кловского Д.Д., – М., Радио и связь 2000, 797с.

3. Майстренко В.А. Статистические методы приема и обработки сигналов в системах радиосвязи. Руководство к решению задач / В.А.Майстренко, В.Ф.Попов. – Омск: Издательство ОмГТУ, 2008 – 101 с.

4. Кислов В.Я. Новый класс сигналов для передачи информации. Широкополосные хаотические сигналы / В.Я. Кислов, В.В. Кислов. - Радиотехника и электроника, 1997, том 42, №8, с.962-973.

5. Стельманенко Б.Г. Нелинейные псевдослучайные последовательности в широкополосных системах передачи информации / Б. Г. Стельманенко П. Г. Тараненко. – Зарубежная радиоэлектроника, №9, 1988 , с.3 – 16.

6. Olsen, J.D. и др.-IEEE Trans., 1982, v. IT-28, №6.

7. Blahut R.E. Theory and practice of error control codes. – Addison – Wesley Publishing Company Reading, Massachusetts, 1984.

8. Журавлев В.И. Использование свойств децимации и редецимации М -последовательностей в радиосистемах /В.И. Журавлев, А.Б.Царев. –Радиотехника, 1990, №10, с.8-11.

9. Кислов В. Я. Корреляционные свойства шумоподобных сигналов, генерируемых системами с динамическим хаосом / В. Я. Кислов, В. В. Калмыков, Р. В. Беляев, Г. М. Воронцов. - Радиотехника и электроника, 1997, том 42, №11, с.1341-1349.

10. Кальянов Э.В. Преобразование регулярных колебаний в хаотические / Э. В. Кальянов. - Радиотехника и электроника, 2004, том 49, №12, с.1492-1499.

11. Гуляев Ю.В. Широкополосные телекоммуникационные средства с кодовым разделением каналов на основе хаотических сигналов. / Ю. В. Гуляев, В. Я. Кислов, В. В. Кислов и др. - Радиотехника , 2002, №10, с. 3-15.

12. Беляев Р. В. Спектр периодов псевдослучайных последовательностей, формируемых дискретным алгоритмом с запаздыванием. / Р. В. Беляев, Г. М. Воронцов, В. В. Кислов и др. - Радиотехника и электроника, 2004, том 49, №3, с.325-332.

13. Замарин А.И. Многоуровневые числовые последовательности для формирования сигналов с псевдослучайной перестройкой рабочей частоты в системах передачи информации и радиолокации / А.И. Замарин, А.В.Андреев. – Зарубежная радиоэлектроника, 1993, №5, с.3-11.

14. Майстренко В.А. Статистические методы приема и обработки сигналов в системах радиосвязи. / В.А. Майстренко, В.Ф. Попов. – Учебное пособие. – Омск: издательство ОМГТУ, 2009–119с.

15. Лёзин Ю.С. Введение в теорию и технику радиотехнических систем. /Ю.С. Лёзин. – Учебное пособие для высших учебных заведений. –Москва: Радио и связь, 1986–279с.

16. Попов В.Ф. Эффективность одного алгоритма выбора рабочих частот в радиолинии с частотно-временными сигналами / В.Ф. Попов. – Техника средств связи, серия Техника радиосвязи, выпуск 10,1984, с.3–11.

17. Гантмахер В.Е., Быстров Н.Е., Чеботарев Д.В. Шумоподобные сигналы. Анализ, синтез, обработка. / В.Е. Гантмахер, Н.Е.Быстров, Д.В. Чеботарев. – СПб.: Наука и Техника, 2005. – 400с.

Приложение